こんにちは、眠る亀です。
「2数を解とする2次方程式」で簡単に解く別の解法はないかなぁと考えていたら、面白いものを思いつきました。今回はそれを紹介したいと思います。
自問

回答
この問題を解く場合、教科書にもチャートにも、というかどの問題集にも解と係数の関係を用いた解法ばかりが載っています。私の方法と比較するために、その方法を追ってみようと思います。
まず、解と係数の関係とは次のような関係のことでした。
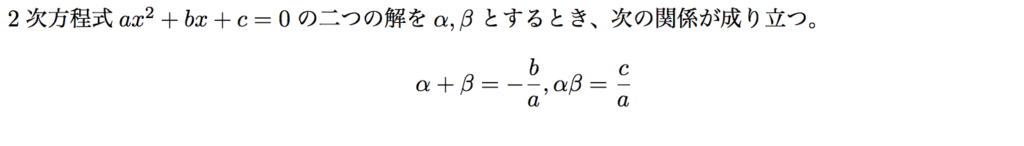
この問題に適用します。x^2-7x-3=0の二つの解に関して、解と係数の関係を用いると、以下の関係が求まります。
α+β=7, αβ=-3
ここで、求めたい2次方程式について、解と係数の関係の逆を使うことを考えましょう。すなわち、(α-1)+(β-1)の値と(α-1)(β-1)の値の両方がわかれば、求める2次方程式の係数を求めることができる、ということです。2次方程式の1つを求めることができれば良いので、2次の項の係数を1とするものを求めれば良いです。すなわち、求める2次方程式をx^2+Bx+C=0と置くと、B, Cは次で求まります。
(α-1)+(β-1) = -B, (α-1)(β-1) = C
そこで、これらの値を求めます。
-B = (α+β)-2 = 5
C = (αβ-(α+β)+1) = -3-7+1 = -9
以上より、求める2次方程式の一つは、x^2-5x-9=0となります。
さて、これ以外の解法は普通、載っていませんよね。しかし、解と係数の関係を学んだ方なら、この方法を圧倒的に超える当意即妙の方法を思いつくはずなんです。解と係数の関係を学ぶ前に、通常は2次関数を学んでいるはずです。ここで、2次関数の知識を用いるとこの問題を一瞬で解くことができます。
さて、皆さんももう一度考えてみてください。とても単純な方法です。発想の原点は、イメージでした。二つの解がともに-1だけずれている、というのがポイントです。そして、2次方程式の解というのは、2次関数とx軸との交点のx座標のこと、、、。
さて、そろそろ明かしましょう。方法は、
2次関数の平行移動です。
よく考えてみると、解が-1だけ動くというのは、2次間数上の2点がx軸に対して同じように動くことを指しています。これを実現する移動手段は、2次関数の場合「平行移動」しかありえません。
すなわち、この問題は2次方程式の左辺に現れる2次式をx方向に-1だけ平行移動した関数を求めることと同じです。その関数とx軸との交点が(α-1, β-1)になっているのです。よって、以下の式変形で求められます。
(x+1)^2-7(x+1)-3 = x^2-5x-9
ゆえに、求める方程式はx^2-5x-9=0となります。
どうでしょう? 同じ解法を思いついた方はたくさんいると思いますが、私の周りではみなかったので、ここで紹介しておこうと思います。
今回は、当意即妙解により、驚くほど簡単に求められました。出題者の意表を突いた解答というのは、このように解法をエレガントにすることに一役買うことが多いです。学校の解説が退屈だなぁと思っている方は、そんな解法を探して、先生や周りの生徒を驚かせてみるのも面白いですよ。
本日も最後までお付き合いくださり、ありがとうございました。

コメント