文字を含む4次方程式と実数解の個数

こんにちは、眠る亀です。
知恵袋にて、質問のあった数学の問題について回答します。ちょっと自信ありませんが、間違えていれば訂正します。

質問

aを実数とする。xの4次方程式
(x^2-ax+1)^2-a(x^2-ax+1)+1=x
を満たす実数解の個数が次のようになるようなaの範囲を求めよ。
(1)4個
(2)2個
(3)3個

回答

この式を見て、真っ先に行いたくなるのが「置き換え」だと思います。何も考えず、次のように置き換えてみます。

この式をぼぉ〜と眺めていると、ただ綺麗だなぁと思うくらいなんですが、グッと睨むとこの二つの式がXとxの対称式になっていると気づくはずです。対称式に対する定石は、「辺々引く」ことです。そこで、辺々引いた式を書いてみると次のようになります。

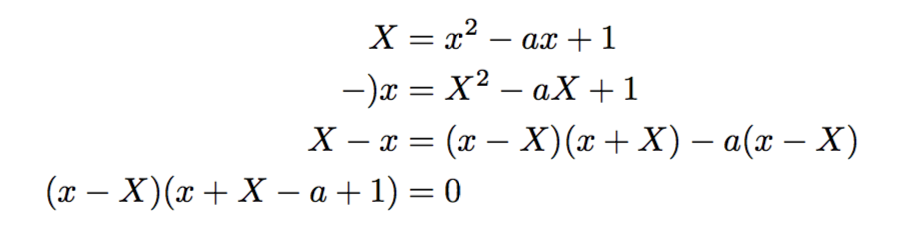
この式変形から、X=x, X=-x+a-1という必要条件が導かれます。これらが求められたので、最初の置き換えに戻ります。例えば、X=x^2-ax+1のXにこれらの条件を代入すると、以下の二つの式が求められます。

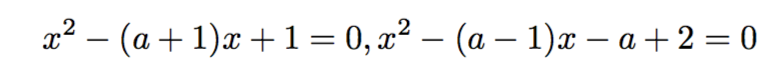
これらの解が、最初に与えられた4次方程式の解となるわけです。左の式を式A, 右の式を式Bと置きましょう。さて、問題は実数解の個数が4個、2個、3個になる場合を考えなければならない、ということです。例えば、実数解の個数が4個になる場合は、式Aから異なる2個の実数解、式Bから異なる2個の実数解を得られれば良い、と考えたくなります。概ねそういう方向なのですが、一つ気をつけないといけないのは、式Aと式Bから出てくる実数解が一致してしまうことがないのかどうか、ということです。つまり、式Aと式Bで解が重複してしまうと、解の個数がずれてしまうということです。これが面倒なので、先に調べておきましょう。

求め方は単純で、式A, Bに共に成り立つ値をx0などとおき、二つの式からx0をaの式で表します。そのx0を式A, Bのどちらかに代入すれば、実数解が一致してしまうときのaの値を求めることができます。次のように計算します。

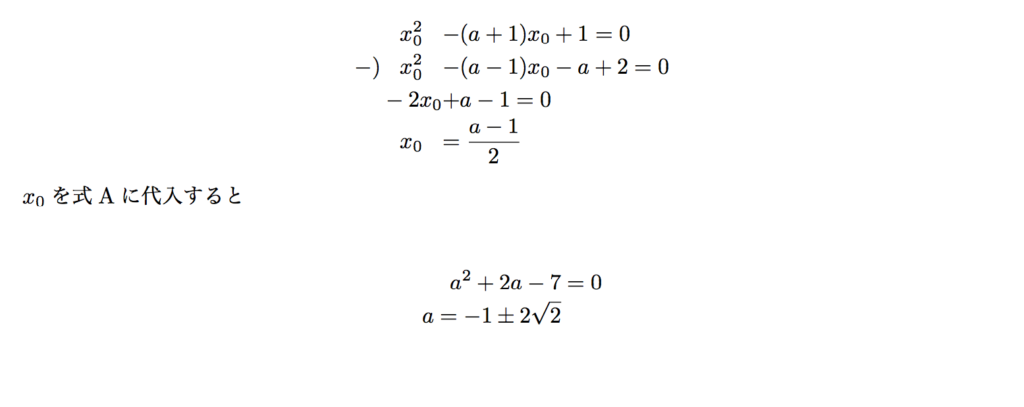
これらの計算により、a=-1±2√2のときには、式A, 式Bの実数解が一致してしまうことがわかりました。このaの値に注意して、実数解の個数を求めます。

(1)実数解の個数が4個

基本的には式A, Bともに異なる実数解を2つ持てば良いので、それぞれに判別式をDa, Dbとして以下のような条件が求められます。

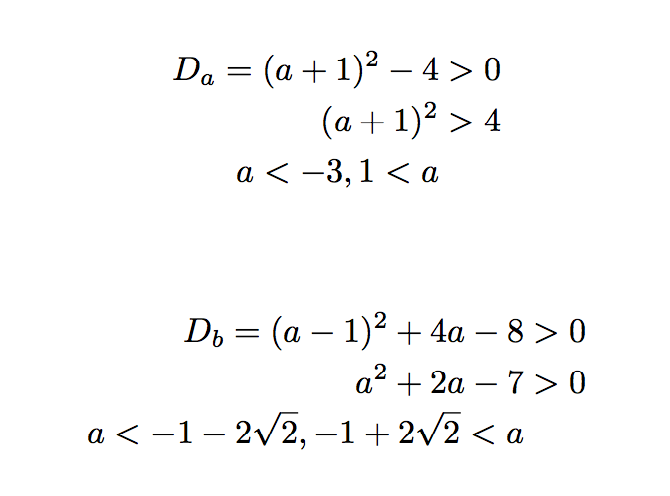
これらの範囲を図示すると、次のようになります。

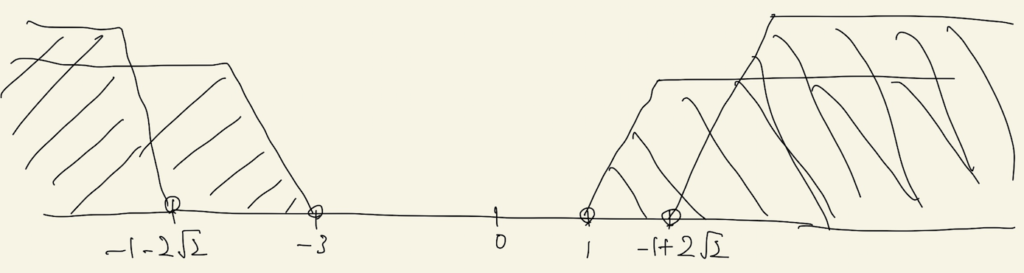
さて、先ほど気にしていた式A, 式Bの実数解が一致してしまう状況は、a=-1±2√2ですが、ちょうど除外されているので、ここでは気にしなくて大丈夫です。よってこの場合のaの範囲は、以下です。

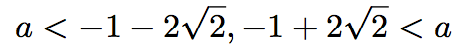
（2)実数解の個数が2個

上の範囲を見ながら考えると、可能性は次の通りです。

1. 式Aの実数解が2つかつ、式Bの実数解が0
2. 式Aの実数解が1つかつ、式Bの実数解が2つ

1の方はわかりやすいと思います。2の方を見て、実数解が3個じゃんと思うかもしれませんが、これはa=-1±2√2の特殊な場合を指します。つまり、式Aは異なる二つの実数解を持ちながら、そのうちの片方と式Bの重解が一致するような状況です。これで、異なる実数解の個数は2種類となります。よってaの範囲は、以下です。

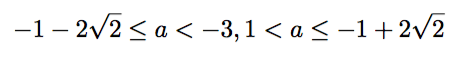
(3)実数解の個数が3個

さて、実数解の個数が3個になる場合ですが、式A, Bについて次のような可能性があります。

1. 片方が重解で、片方が異なる二つの実数解かつ、解を共有しない。
2. 両方が異なる二つの実数解を持つが、1つだけ解を共有する。

今までの議論から、この場合、二つとも起こり得ないですね。よって、解はなしです。

まとめると、次のようになります。

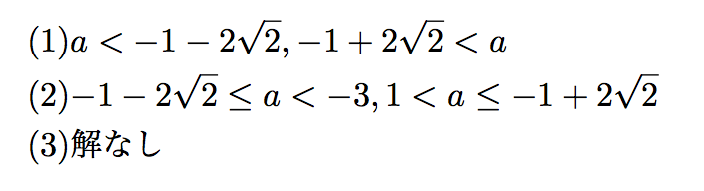
どうでしょうか。