眠る亀です。今日は、関数の解の個数を定数分離法を用いて解く問題に関して、知恵袋で質問を見つけましたので回答します。よろしくお願いします。
質問

回答
非常に丁寧な誘導がついています。出題者がこの問題で解答者に取得してもらいたい技術は、定数分離法と呼ばれる手法です。定数分離法を説明するために、もっと簡単な例を持ってきます。例えば、次のような問題はどうでしょうか。
問題 x>0の範囲で、x^2 – 2x – a + 1 = 0の解の個数が2個になるようなaの値の範囲を調べよ。
この問題をf(x) = x^2 -2x – a +1として解こうとすると文字と変数が混合していて面倒です。そこで、定数と変数を分離することを考えます。これを
x^2 – 2x +1 = a
と書き直して、求める解を「x^2 – 2x – a + 1 = 0の解」と考えるのではなく、「y=x^2 -2x +1とy=aのグラフの交点のx座標」と考え直します。これらは同じ意味ですが、後者の方が目で見て解の個数を調べられるので得です。それぞれのグラフを書くと、次のようになります。
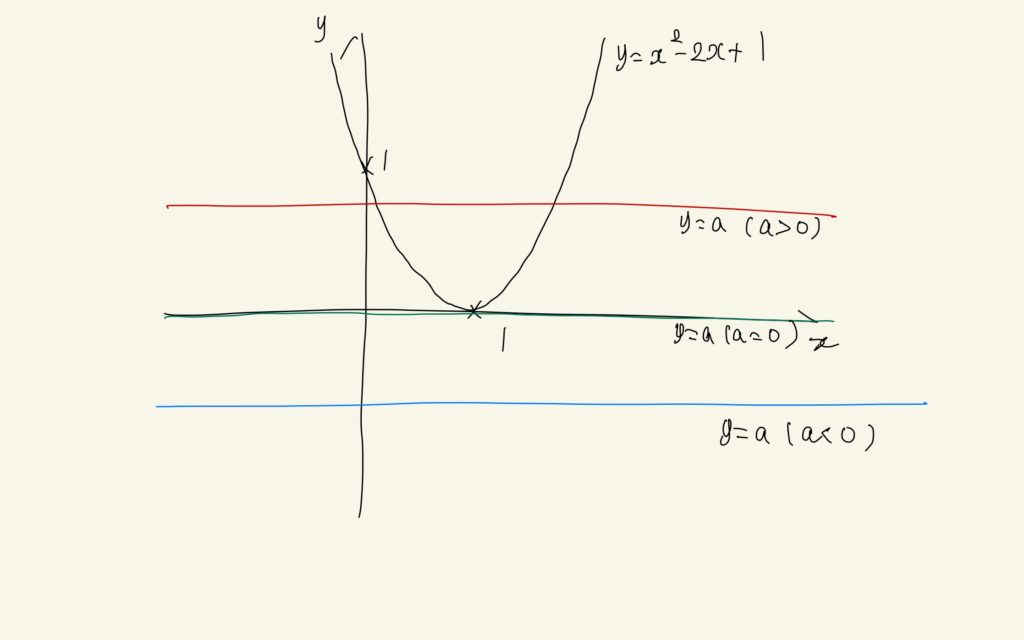
上の図1のように、a>0のときy=x^2 -2x +1とy=aのグラフの交点のx座標の個数は2個になります。それ以外は条件を満たさないので答えは、a>0となります。
この考え方を数Ⅲで学ぶ関数に応用したものが本問です。それでは、(1)から解いていきます。
(1)
増減を調べるときは、yを微分してその符号を調べます。ただし、定義域(xの範囲)に注意します。今の場合、logxが含まれているので、xの範囲は「全ての実数」ではなく、x>0に限定されます。このことを考慮に入れて微分の計算を行い、増減表を書きます。

3段目から最後の段に進むときに分母・分子をxで割っていますが、これはx>0であるために可能になります。もし、x=0となるような状況ではxで割ることはできません。y’ = 0としてxを求めると、2logx = 1 ↔︎ logx = 1/2 ↔︎ x = e^{1/2} = √eと計算できます。この計算から、増減表を書くことができます。増減表がかければ、図2のようにグラフを書くこともできます。
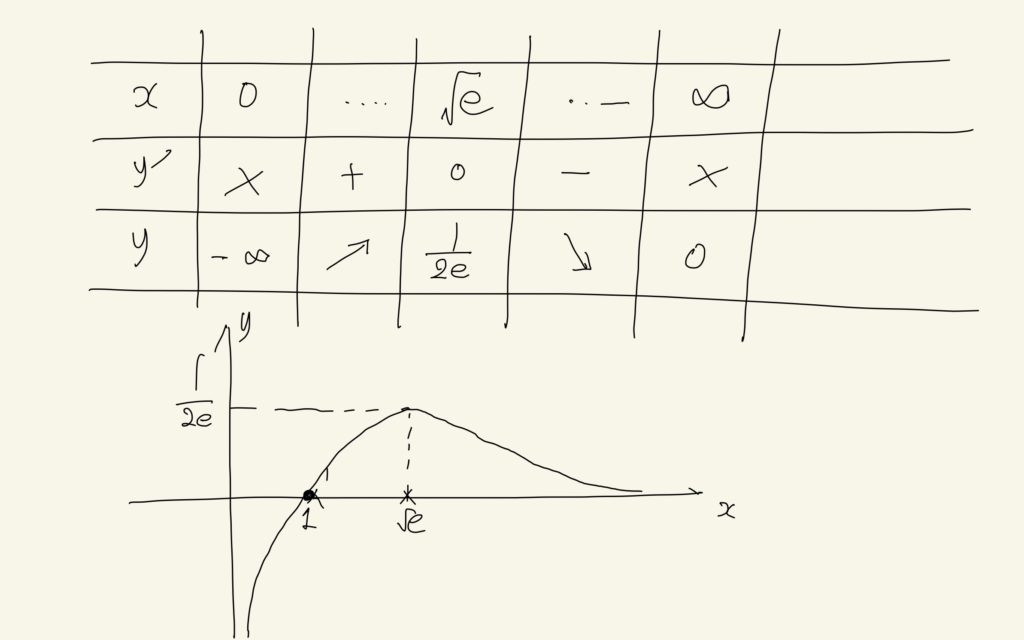
数Ⅲでは、何も指定がなければ定義域を∞に広げて考えるのが普通です。∞にいくときの計算は、本来は自分で行うのですが、本問にはすでに答えが書いてあるので、それを使います。この関数は、x->∞でy->0に収束するような関数であることがわかります。ちなみに、x=0付近のyの値ですが、logxがx=0付近で-∞であることと、1/x^2が∞であることから、結果-∞です。
(2)
ここでは、(1)の関数に絶対値をつけた関数のグラフを書きます。絶対値をつけたグラフは、その中身の関数の形がわかっていれば、とても簡単に書けます。というのも、中身の関数のグラフで「負になっている部分をx軸に関して対称に裏返す」だけで済むからです。すなわち、求めるグラフは図3の実線部分です。
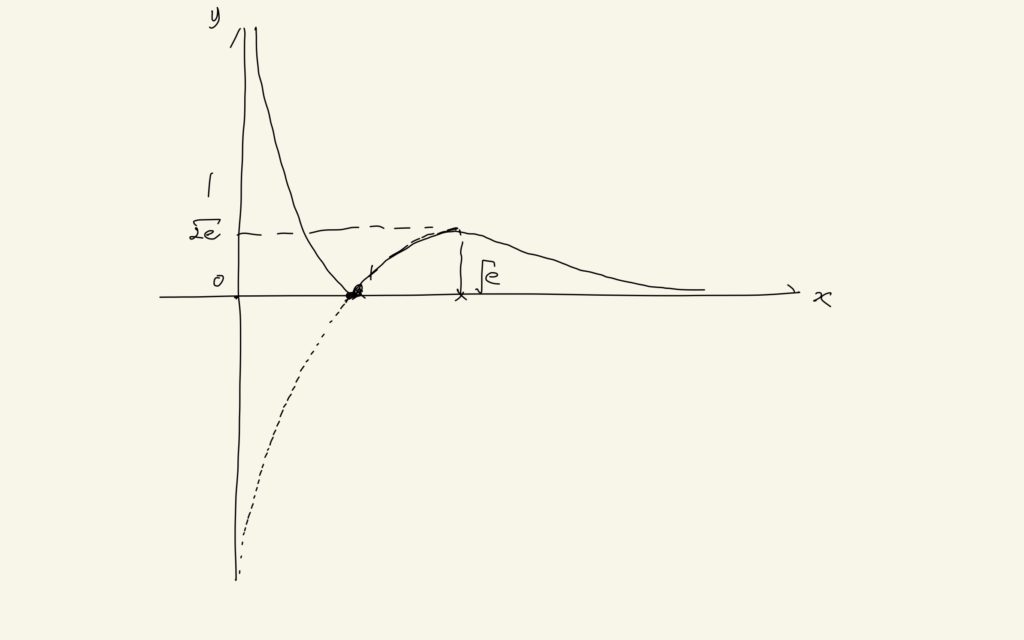
図3の点線部分は、裏返す前の(1)のグラフの残像を示しています。
(3)
(1), (2)が(3)を解くための用意周到な準備となっていました。ここからが本番です。と言ってもやることは定数を分離するだけです。今の場合、定数はkですのでこの文字と変数xを分離してやります。
- kx^2 -|logx| = 0
- kx^2 = |logx|
- k = |logx|/x^2 (x>0)
2から3にいくときに、x^2で割りましたが、これは先ほど言ったようにx>0でxが0にならないからです。3の右辺は(2)の関数と全く同じですね。求める解の個数は、y=kとy=|logx|/x^2 の二つのグラフの交点のx座標の個数と同じです。今までに、y=|logx|/x^2のグラフを書くことができていますので、あとはkを変えた時に、交点がどのように変わるかを見てやればよいです。

図4に、色々なkでの二つのグラフの交点関係を示しました。
- k>1/2e (青)のとき、交点の個数は1個
- k=1/2e (紫)のとき、交点の個数は2個
- 0<k<1/2e (赤)のとき、交点の個数は3個
- k=0 (緑)のとき、交点の個数は1個
- k<0 (オレンジ)のとき、交点の個数は0個
以上より、求めるkの値の範囲は0<k<1/2eとなります。
いかがでしょうか。

コメント