こんにちは、眠る亀です。
今回は、質問というか、知恵袋に出題された創作問題を解きます。
問題
問題を作ったので、解法の回答、評価、アドバイスをお願いします。
(1)y=1/xが0<x<1で下に凸であることを示してください。
(2)xe^x=1の解をαとするとき、
(-3+√17)/2<α<1/√3を満たすことを示してください
想定レベルはやや難〜難くらいだと思います。
回答
(1)は初等関数を二階微分すれば解決します。

(2)が面白い問題ですね。面白いですが、それにふさわしいエレガントな回答を思いつかなかったのが残念です。自分、割とパワフルな回答も好きなので、数値計算でゴリゴリ攻めました。

まず、f(x)の凸性を確認します。一応、これはあとで効いてきます。

両辺を8倍、というのはもちろん2, 3, 4, 5…と試した結果です。頭の中では、17*a^2 = X^2 + 1となるようなaはないかなぁと考えていました。別に1ではなくても小さい数ならそれで良いと思っていましたが、8倍すると想定通りのものが出てきてちょっと驚きました。こういうものが出てくると、もう他の解法が考えられないんですよね。
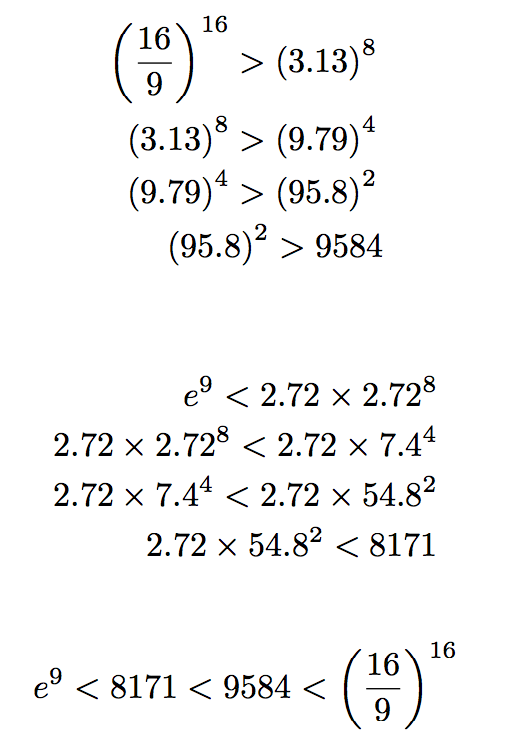
この条件は、f(9/16)<0すなわち、(-3+√17)/2 < 9/16 < αというわけで、数値計算(ちゃんと頭と手でやりました)により左辺側が示されました。

以上で、題意を示したことになります。この解法、エレガントのかけらもないなぁ。そして、(1)を使えていない……。

コメント