絶対値と文字を含む定積分の最小値

こんにちは、眠る亀です。
知恵袋の回答にお答えします。新しいカテゴリーを作成以降、初の投稿となります。知恵袋の回答を「矢風出張」にまとめました。

質問

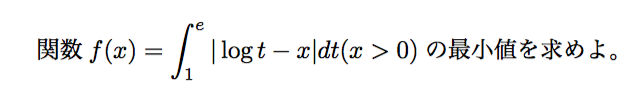
回答

定積分の中に、絶対値と積分変数以外の文字が含まれているとき、ほとんどの場合、場合わけが必要です。この問題ではx>0としていますが、せっかくなのでx≦0のときについても考えてみます。ここで、積分変数が”t”であることに注目です。xは「この積分を計算する上では」定数のようなものだと考えます。普段、xは変数としてしか考えないので、少しこんがらがるかもしれませんが、ここでは頭の切り替えが必要です。

さて、この絶対値をどのように外すのか。それが最大の問題です。絶対値はその中身が負であればマイナスをつけて外し、その中身が正であればそのまま外すという性質のものでした。今気にすべきなのは、tが1からeまで動くとき、logtがどのような振る舞いをするか、です。logtは単調増加関数で、t=1のとき0, t=eのとき1をとります。ゆえに、この問題の範囲では、logtは0から1まで単調に増加する、という振る舞いをします。すると、xの値を次のように場合わけする必要があることに気づきます。

1. x<0
2. 0≦x<1
3. 1≦x

(1) 1の場合

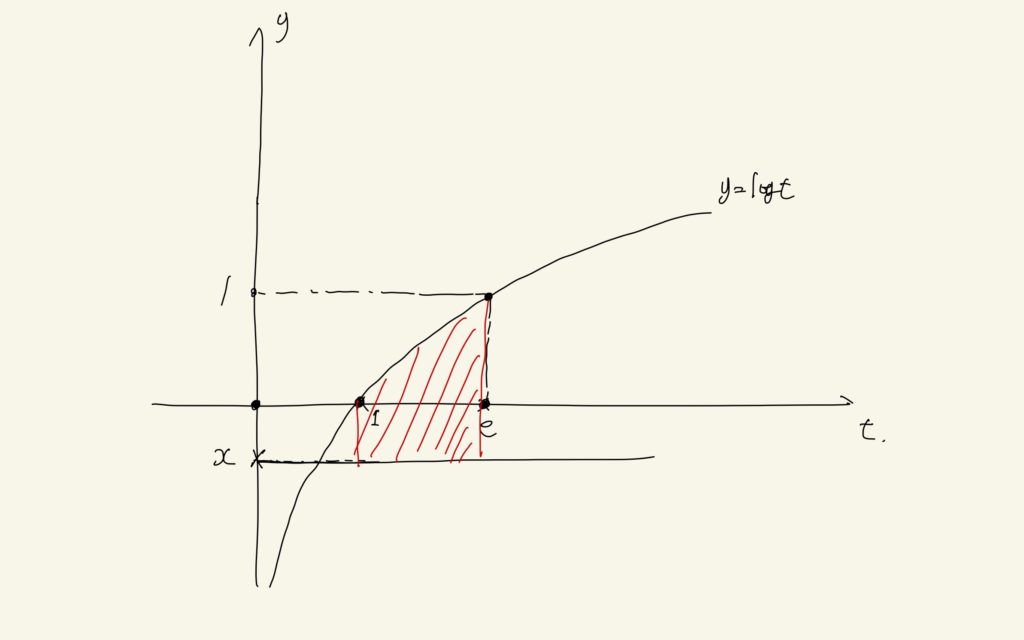
x<0のとき、絶対値の中身logt-xは、常に正の値を取ることがわかるでしょうか。すなわち、絶対値はそのまま外して計算します。

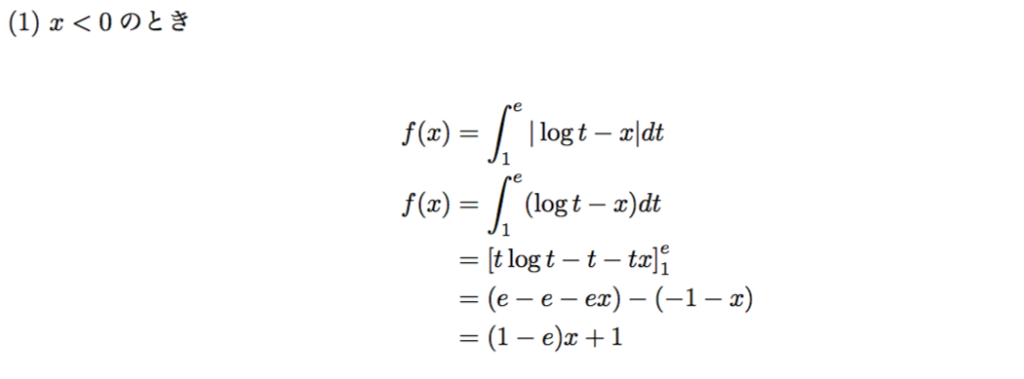
しかし、この問題の範囲では、x>0のみを考えるので、この式はこの先使いません。

(2)２の場合

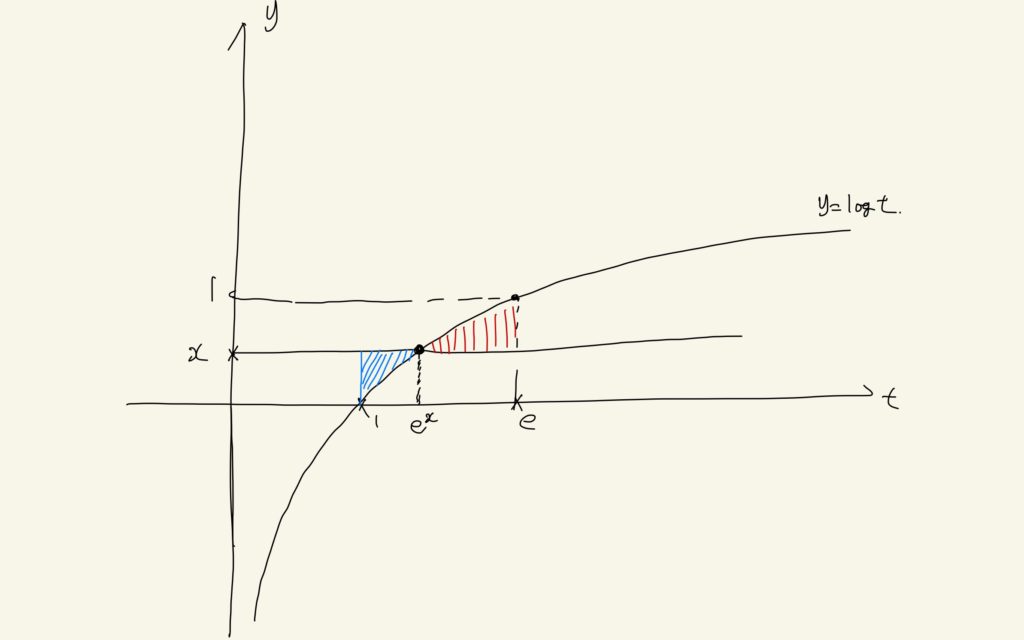
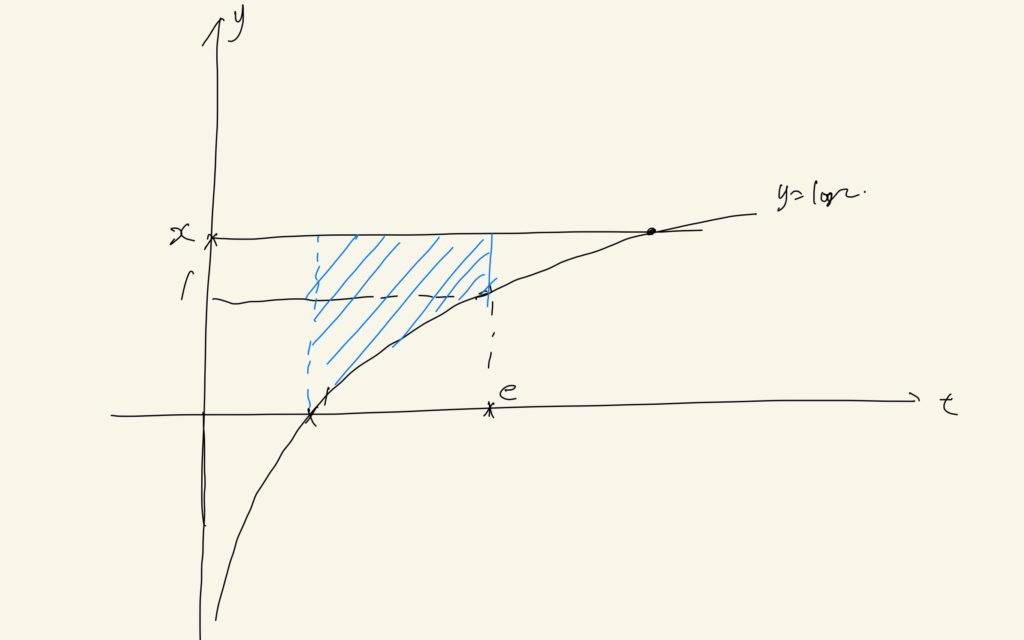
0≦x<1のときは、xの値によってlogt-xが負になることがあります。上の図のように、logt=x、すなわちt=e^xが分岐点です。このtより小さいときにはlogt-xは負、それより大きいときは正です。よって次のように計算します。

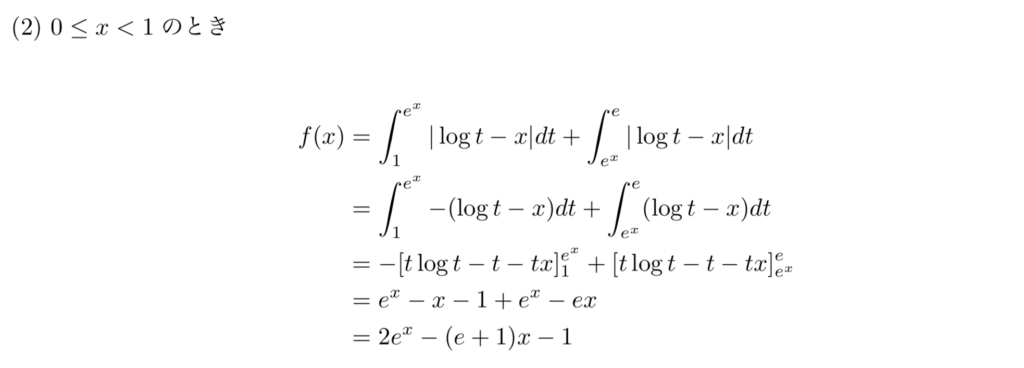
(3)３の場合

1≦xのときは、上の図のようにlogt-xは常に負になります。よって、次のように計算します。

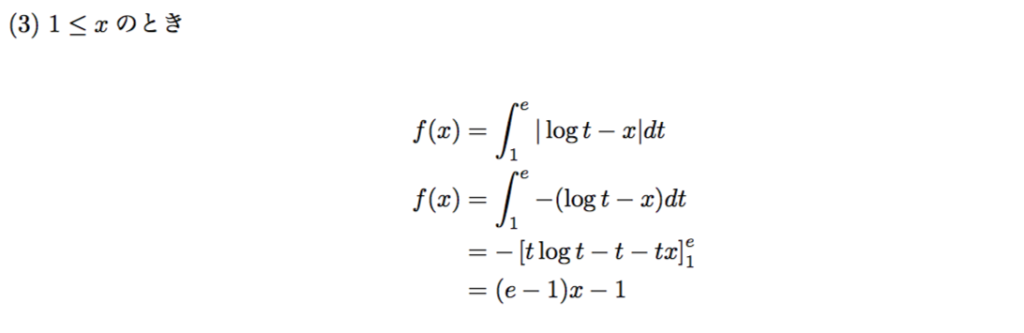
(2), (3)をまとめると、

1. 0<x<1のとき、f(x) = 2e^x -(e+1)x -1
2. 1≦xのとき、f(x) = (e-1)x-1

です。後は、y=f(x)の振る舞いをみます。y=f(x)をxで微分して増減表を調べます。

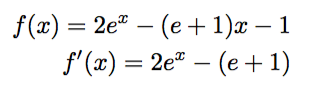
f'(x)=0となるxをαとおくと、f(α) = e+1 – (e+1)log((e+1)/2) -1 = e-(e+1)log((e+1)/2)となります。また、y=f(x)の増減表は以下です。

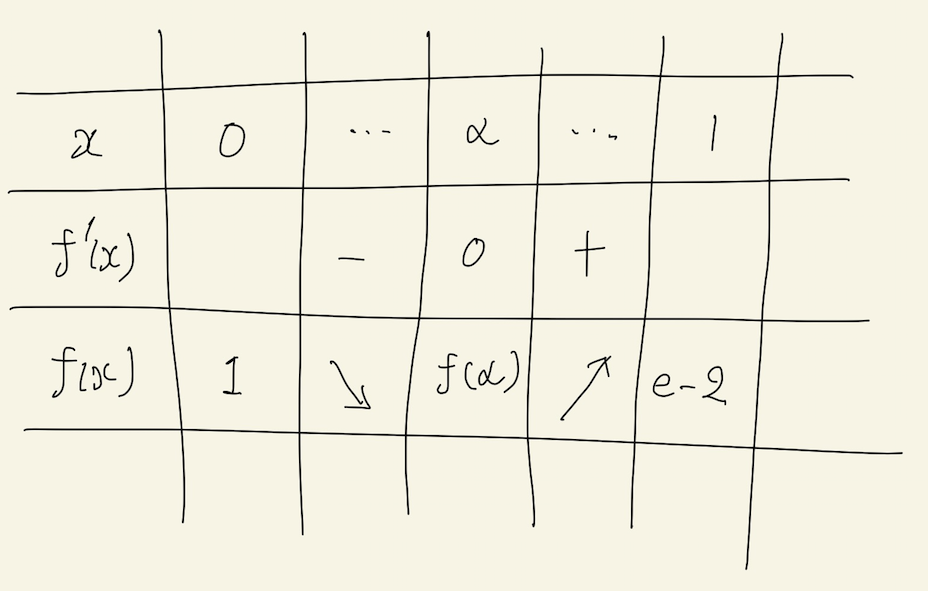
このことを考慮すると、最終的にx>0でのy=f(x)のグラフを書くことができます。

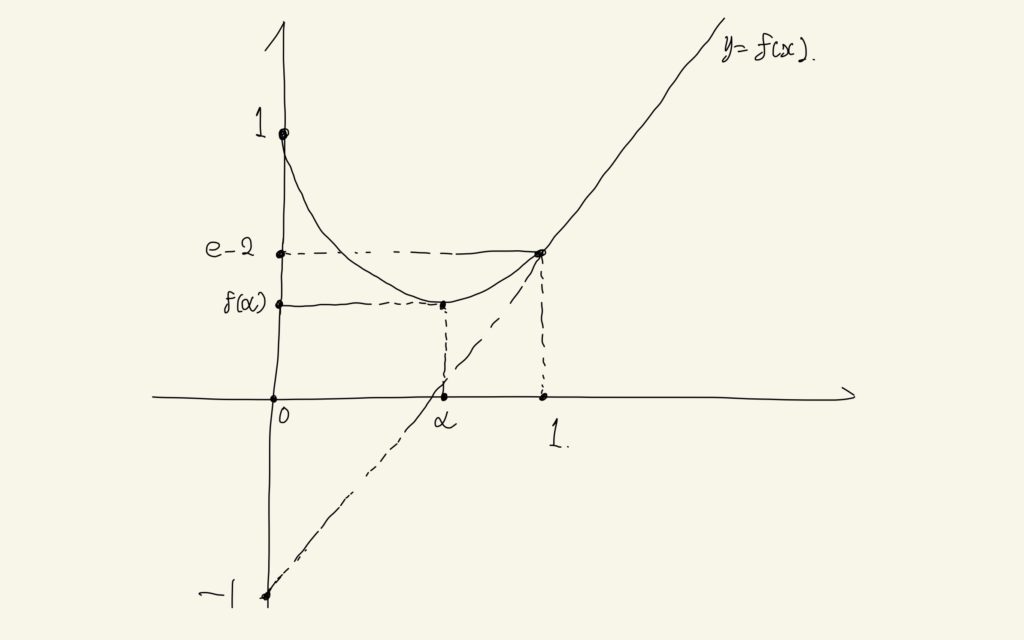
このことから、y=f(α)が最小値となることがわかります。ゆえに、求める最小値は

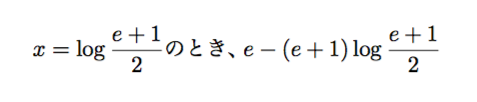
いかがでしょうか。