拙ブログでは「必要性と十分性の概念とその適用」という題名で記事を書きました。そこで、放物線と円が交わる条件に関する質問をいただいたので、その質問にお答えする形で記事を書いていきたいと思います。
放物線と円が交わる問題です。質問者様の悩みどころを要約すると以下のようになります。
- 2式から\(x\)を消去した2次方程式が重解を持つことと\(D=0\)は同値か。
- 2式から\(x\)を消去した方程式の判別式\(D=0\)と、円と放物線が接するということは同値ではないのか。もし同値ではないのなら、\(D=0\)を使って解答をして良いのか。
- 解答では、”この2次方程式は重解をもつので\(D=0\)で\(a=-\frac{37}{4}\). このとき2次方程式の解は\(y=-1/2\)で\(-3\leq y\leq 3\)を満たす(質問では、\(-3<y<3\)とありましたが、等号がついていなかったでしょうか)”とある。つまり、\(a=-\frac{37}{4}\)を代入して確認していることから、「この2次方程式は重解を持つこと」は答えとなるための必要条件だったのか。
以上の質問に答えながら、この問題に取り組みたいと思います。
はじめに、今の場合で放物線と円が接する状況を分析すると以下の(イ)(ロ)(ハ)の3通りが考えられます。
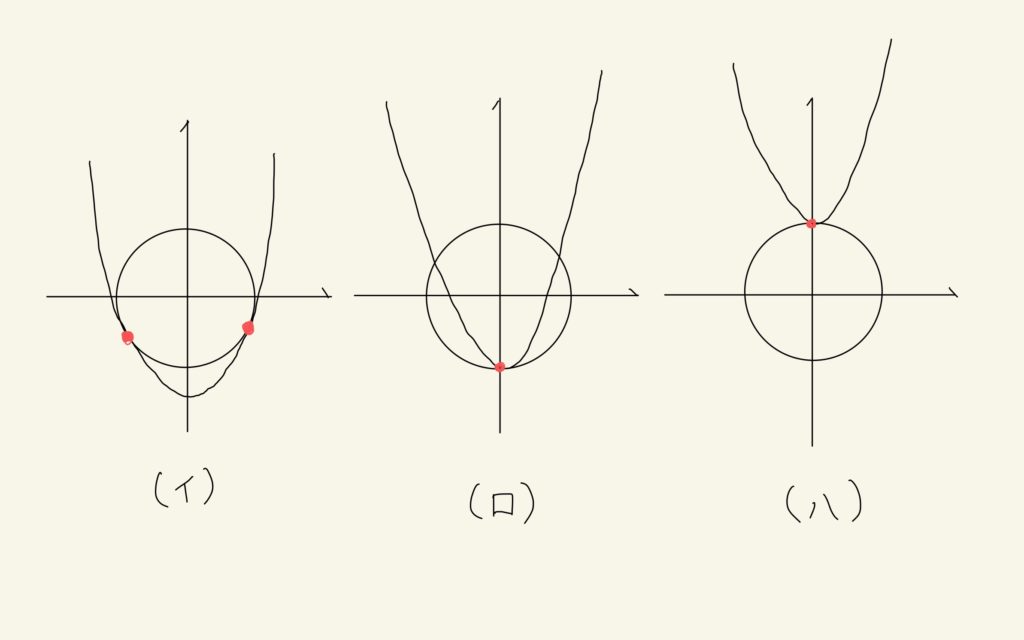
- 2式から\(x\)を消去した2次方程式が重解を持つことと\(D=0\)は同値か。
一般に2次方程式\(ax^{2}+bx+c=0\)が重解を持つことと\(D=0\)が成り立つことは同値です。というのも2次方程式の解は
$$x = \frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$$
であり、\(D = b^{2}-4ac\)と定義しているので、\(D=0\)となることと重解(2つの同じ解)となることは同値です。
- 2式から\(x\)を消去した方程式の判別式\(D=0\)と、円と放物線が接するということは同値ではないのか。もし同値ではないのなら、\(D=0\)を使って解答をして良いのか。
2式から\(x\)を消去した方程式とは今の場合\(y^{2}+y-a-9=0\)のことを指していると思います。この式の判別式\(D\)が0になることは、円と放物線が接することと同値であるかという問題です。結論から申し上げると、「同値ではない」と言えます。同値であるというのは、必要条件でもあり、十分条件でもあるということですが、今の場合以下の二つが成り立つことを言います。
- \(y^{2}+y-a-9=0\)の判別式について\(D=0\)ならば円と放物線が接する。
- 円と放物線が接するならば\(y^{2}+y-a-9=0\)の判別式について\(D=0\).
このとき、1の命題は\(y \geq a\)という条件が満たされている限り、成立します。数学的な同値変形でも証明できると思いますが、より視覚的にこれを説明します。\(y^{2}+y-a+9=0\)を変形して\(a = y^{2}+y+9\)と置き、\(z = y^{2}+y+9\)のグラフを書いてみます。
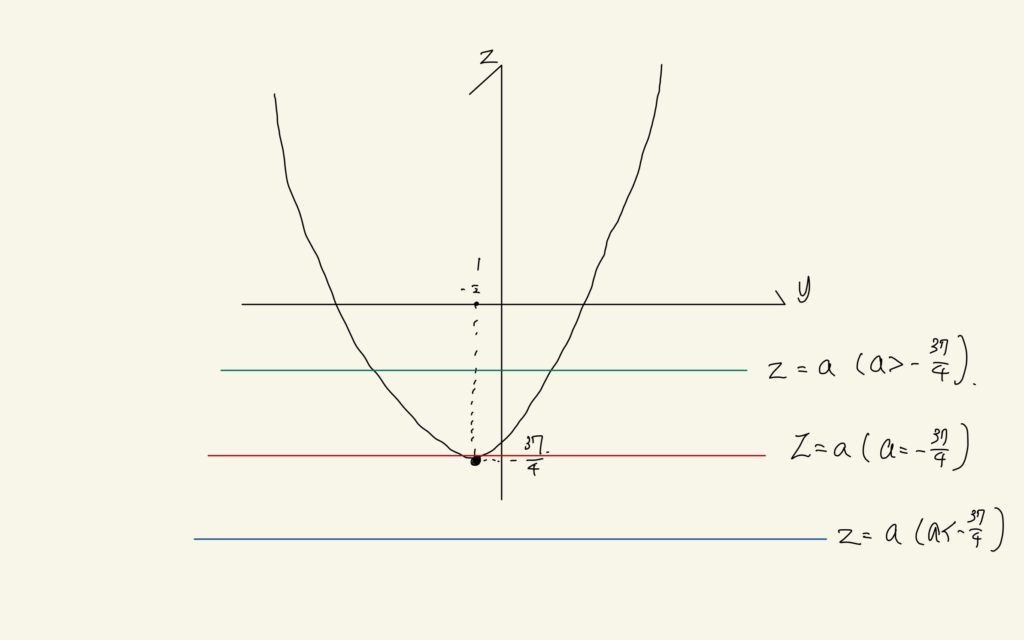
ここで、\(z=a\)と\(z =y^{2}+y+9\)のグラフの交点が\(y^{2}+y-a+9=0\)の解となっています。\(y\)に関するこの2次方程式が重解を持つこと(\(D=0\))となることは\(z=a\)と\(z =y^{2}+y+9\)との交点の\(y\)座標がただ一つ決まることと同値なので、\(a = -\frac{37}{4}\)のときです。この場合では、\(y \geq a\)が満たされています。さて、ここで\(a\)をプラスとマイナスの方向に少しずつずらしたものを考えます。
(1)\(a\)を少しマイナスにずらしたとき(青線の場合)
この場合は、\(z=a\)と\(z =y^{2}+y+9\)に交点がありません。交点がない状況とは、もとの放物線と円に戻れば放物線が円の下側にきてしまって交点がない場合か、放物線が円の上側にきてしまって交点がない場合をさします。
(2)\(a\)を少しプラスにずらしたとき(緑線の場合)
この場合は、\(z=a\)と\(z =y^{2}+y+9\)に交点が2つあります。今の場合で交点が2つある状況とは、もとの放物線と円に戻れば上にあげた(イ)と(ロ)の場合の間で、交点が全部で4つある状況をさします。
\(a\)を少しプラスとマイナスにずらしてこのような違いが生じるのは、\(a = -\frac{37}{4}\)のときに二つの放物線と円が2交点で接している状況しかありません。すると、\(z=a\)と\(z =y^{2}+y+9\)との交点の\(y\)座標がただ一つ決まり、その\(y\)が\(y\geq a\)を満たすならば、問題の円と放物線は2点で接しているということができます。そして、\(z=a\)と\(z =y^{2}+y+9\)との交点の\(y\)座標がただ一つ決まることは\(y^{2}+y-a+9=0\)の判別式について\(D=0\)が成り立つことと同値なので、結果的に、\(y^{2}+y-a+9=0\)の判別式について、\(y \geq a\)かつ\(D=0\)が成り立つならば問題の円と放物線は2点で接すると言えます。
2次方程式\(x^{2}+y^{2}=9\)は\(x^{2} = y-a\)という式を代入することによって得られているので、\(y\)はどのような値でも良いわけではなく、\(y \geq a\)となることが必要だというのがポイントです。\(D=0\)だけでは、\(y \geq a\)までは保証できていないわけですね。
ところで、\(y \geq a\)という条件をもう少し掘り下げていきます。これは一体何を言っているのかというと、実は\(x\)は実数だと主張していることと同値です。\(y \geq a\)を要求するということはもとを辿ってみると\(x^{2} = y-a \geq 0\)が成り立っていることからきています。
- \(x\)が実数ならば\(y \geq a\).
- \(y \geq a\)ならば\(x\)は実数
複素数の世界では、このどちらも真の命題なので、\(x\)が実数であることと、\(y \geq a\)は同値です。\(x\)が虚数ならばまたその時に限り、これは成り立ちません。\(x = i\)を代入してみれば、これが成り立たないことがすぐにわかると思います。また\(x\)が実数であるとき、円の方程式から\(x^{2} = 9-y^{2} \geq 0\)となるので、\(x\)が実数であることと、\(y\)が実数で\(9-y^{2} \geq 0\)つまり、\(-3\leq y\leq 3\)が成り立つことは同値です。このことが最後の質問に効いてきますので、頭の片隅においておくと良いかと思います。
さて、では2の条件(円と放物線が接するならば\(y^{2}+y-a-9=0\)の判別式について\(D=0\))の方はどうでしょうか。これは、反例をあげることができます。円と放物線が接しているというのは質問者様も即答しているように、例えば、\(a=3\)の場合があります。このとき、\(y^{2}+y-a-9=0\)は\(y^{2}+y-12=0\)となり、この判別式は\(D = 49\)で\(D=0\)ではありません。別の反例として\(a = -3\)があり、このときも\(D\neq0\)です。
以上のことから、2式から\(x\)を消去した方程式の判別式について\(D=0\)になることは、円と放物線が接するための「十分条件」でも「必要条件」でもないようです。しかし、\(D=0\)において、\(y \geq a\)という条件が満たされていれば、2式から\(x\)を消去した方程式の判別式について\(D=0\)になることは、円と放物線が接するための「十分条件」であるが「必要条件」ではないと言えます。どちらにしても、質問者様の先生の指摘は正しいということがわかりました。ちなみに、円と放物線が接するという部分を、「円と放物線が2点で接する」と言い換えると話が少し変わります。この場合は先ほどの議論を辿っていくと、この問題の円と放物線においては、\(y \geq a\)という条件が満たされていれば、2式から\(x\)を消去した方程式の判別式について\(D=0\)になることと円と放物線が2点で接することは同値である、ということができます。
では、2つ目の質問の後半部分で、\(D=0\)を解答として使って良いのか、という議論に移ります。「十分条件」とは「他に答えの候補がある可能性はあるが、それを満たしさえすれば答えの一つとなる」という条件です。ということで、他の候補があったとしても、2式から\(x\)を消去した方程式の判別式について、\(y\geq a\)のもとで\(D=0\)を要求すれば、答えの一つを得ることができます。ゆえに、「\(D=0\)を解答として使って良いのか」という疑問に対しては、「使って良い」ということができます。
- 解答では、「この2次方程式は重解をもつので\(D=0\)で\(a=-\frac{37}{4}\). このとき2次方程式の解は\(y=-1/2\)で\(-3\leq y \leq3\)を満たす」とある。つまり、\(a=-\frac{37}{4}\)を代入して確認していることから、”この2次方程式は重解を持つこと”は答えとなるための必要条件だったのか。
今までのことを総合して考えると、この質問の答えを導き出すことができるかと思います。今までわかったことを整理すると
- \(D=0\)において、\(y \geq a\)という条件が満たされていれば、2式から\(x\)を消去した方程式の判別式について\(D=0\)になること(2次方程式が重解を持つこと)は、円と放物線が接するための「十分条件」であるが「必要条件」ではない
さて、今、円と放物線が2交点で接する条件を求めるために\(D=0\)を要求して答えを求めたとします。重要なことは\(D=0\)だけでは、それが答えとなるための「十分条件」にはなっていないということです。\(D=0\)の時に得られる\(y, a\)の値が\(y \geq a\)となることを確認する必要があります。その確認作業を解答では、「\(y=-1/2\)で\(-3\leq y\leq3\)を満たす」という形で行なっています。なぜそれで良いのでしょうか。それは2つ目の質問の時に掘り下げた、\(y \geq a\)となることの意味を考えればわかります。\(y \geq a\)となることと\(x\)が実数であることは同値でした。また、\(x\)が実数であることと\(y\)が実数で\(9-y^{2} \geq 0\)つまり、\(-3\leq y\leq 3\)が成り立つことは同値です。すなわち、この問題において、実数\(y\)が\(y \geq a\)となることと\(-3\leq y\leq 3\)が成り立つことは同値です。解答では、よりわかりやすい形として、\(-3\leq y\leq 3\)の確認を行ったのだと思います。高校数学では、特に指定がないとき関数で使われている変数は”実数”とみなします。\(y \leq a\)という確認は、\(D=0\)を満たす数が実数であることを確認するプロセスであるということもできます。
以上で、質問者様の質問にお答えしたつもりですが、いかがでしたでしょうか。一つ注意しておきたいのは、ずっと申し上げている通り、\(y \geq a\)かつ\(y^{2}+y-a-9=0\)の判別式について\(D=0\)は答えとなるための「十分条件」なので、他にも候補があることを確認する必要があります。質問者様はすでに1点で接する場合である\(a=\pm3\)を発見されているので問題はありませんが、「必要条件」や「十分条件」をきちんと考えて問題を解いていると、より複雑な問題に対しても同じように「過不足のない解答」を作る技術が高まるかと思います。特に今自分の使っている条件が答えとなるための「必要条件」なのか「十分条件」なのかわからなくなってしまったときは、ここで示したように、「(その条件)ならば(答え)」と「(答え)ならば(その条件)」の二つを試してみると良いと思います。前者だけなら十分条件、後者だけなら必要条件、両方とも満たすならば同値です。もし、十分条件だけで答えを出しているなら、他に答えとなる候補がないかを探す必要がありますし、(一橋の問題で紹介した解法のように)必要条件だけで答えを出しているなら、十分性の確認が必要です。正直、こういうことをいちいち考えて問題を解くのは非常に面倒だし、最初は時間のかかる作業だと思います。私自身もまだまだ完璧に使いこなせているとは思っていません。しかし、簡単な問題から徐々に習慣化していくと良いのではないかと思います。
試しに、\(a=3\)として\(y\)を消去した式を考えると、\(y^{2}+y-12=0\)なので、これを解くと\(y = -4, 3\)が求められます。このうち、\(y \geq a\)となるものは\(y=3\)しかありません。ところでこの時に求められた\(y=-4\)を用いると、\(x\)が実数とはならないことがわかります。このように、放物線と円が1点で交わる場合、方程式は一見重解にならないように感じてしまいます。グラフをみると1点で接していて重解になりそうなのに、方程式ではそうなっていない。このことに少し戸惑いを感じてしまうかもしれません。
この問題を解決してくれるのが別の代入です。今までは\(x\)を消去していましたが、今度は\(y\)を消去してみます。すると
$$\begin{eqnarray}
(x^{2}+a)^{2}+x^{2}&=&9\\
x^{4}+(2a+1)x^{2}+a^{2}-9&=&0\\
\end{eqnarray}$$
で、4次方程式が出てきます。この4次方程式が重解を持つ条件を考えてみます。アイデアとしては先ほども用いた定数分離法です。
$$\begin{eqnarray}
(x^{2}+a)^{2}+x^{2}&=&9\\
(x^{2}+a)^{2} &=& 9-x^{2}\\
x^{2}+a &=& \pm\sqrt{9-x^{2}}\\
a = -x^{2} \pm \sqrt{9-x^{2}}\\
\end{eqnarray}$$
となります。これで\(f(x) = -x^{2} \pm \sqrt{9-x^{2}}\)とおいて、\(y = f(x)\)のグラフを書くことができれば、先ほどと同じように重解の条件を考えることができます。ただ、ここからの計算は数学Ⅲで習う微分法という知識が必要なので、もしまだ微分や数学IIIを未修であれば結果のグラフだけみていただければと思います。
\(f(x) = -x^{2} + \sqrt{9-x^{2}}\)とする
$$\begin{eqnarray}
f^{\prime}(x) &=& -2x + \frac{-x}{\sqrt{9-x^{2}}}\\
&=& \frac{-x(2\sqrt{9-x^{2}}+1)}{\sqrt{9-x^{2}}}\\
\end{eqnarray}$$
この結果から増減表をもとにグラフを書くと以下のようになります。
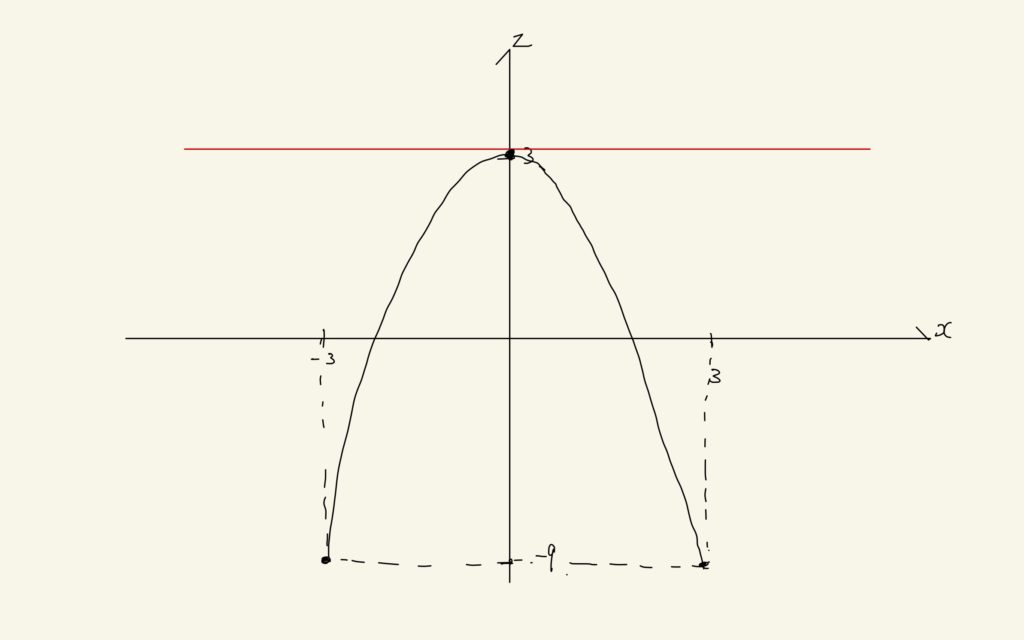
\(h(x) = -x^{2} – \sqrt{9-x^{2}}\)とする
$$\begin{eqnarray}
f^{\prime}(x) &=& -2x + \frac{-2x}{\sqrt{9-x^{2}}}\\
&=& \frac{-x(2\sqrt{9-x^{2}}ー1)}{\sqrt{9-x^{2}}}\\
\end{eqnarray}$$
この結果から増減表をもとにグラフを書くと以下のようになります。
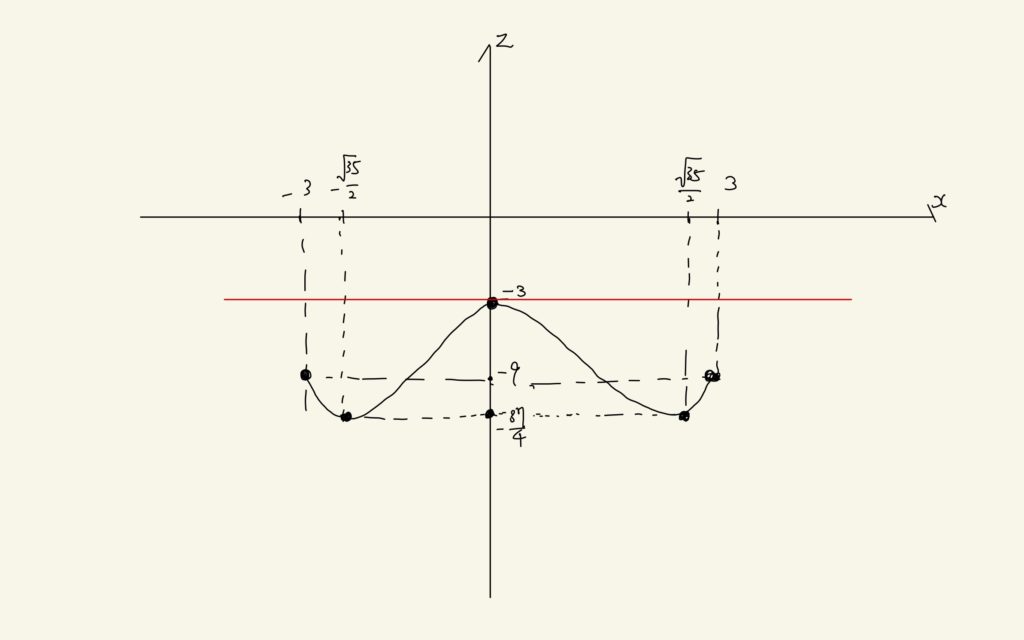
先ほどと同じように、\(z=f(x)\)または\(z =h(x)\)と\(z=g(x)=a\)との交点が4次方程式の解となります。ここで\(a=3\)とすると\(g(x)=3\)と\(f(x) = -x^{2} + \sqrt{9-x^{2}}\)が接する、すなわち重解を持つことがわかります。さらに、\(g(x)=3\)と\(h(x)= -x^{2} – \sqrt{9-x^{2}}\)とは交点を持たないことがわかります。このことを確かめるために\(a=3\)を代入してみると4次方程式は
$$x^{2}(x^{2}+7) = 0$$
なので\(x=0\)が重解となっており、これが唯一の解です。円と放物線の関係をみても、1点で接しており、他の交点はありませんね。
次に\(a=-3\)を考えると、\(g(x)=-3\)と\(h(x)= -x^{2} – \sqrt{9-x^{2}}\)が接するので、重解(二重解)を持つことがわかります。また、\(g(x)=-3\)と\(f(x)= -x^{2} + \sqrt{9-x^{2}}\)からも2つの交点が得られるので、異なる解は全部で3つあることがわかります。実際4次方程式に\(a=-3\)を代入すると
$$x^{2}(x^{2}-5)=0$$
となり、\(x=0\)は重解となっています。
以上のように、\(x\)の4次方程式の形を作れば、円と放物線が接する点は全て4次方程式の重解(この場合は2重解)となるような点であることがわかります。なぜ、重解となる点が円と放物線が接する点になるかを理解するためには、最初に示したように\(a\)を少しプラスとマイナスにずらして、\(z=g(x)=a\)と\(z=f(x)\)または\(z=h(x)\)の交点の振る舞いの変化をみてみれば、わかるかと思います。
追記1
チャート式に書いてある通り、少なくとも「放物線と直線が接する場合」と「円と直線が接する場合」では”D=0⇔それらが接する”という関係が成り立ちます。〇〇と△△に入るものによっては、”D=0⇔それらが接する”という関係が成り立たないことがあるので、このような質問はもっともかと思います。この質問に対する答えを一般化するのは難しいです。というのも、この種の問題を解くときに、判別式\(D\)を用いない方法というのもいくつかあり、そのうちの一つが記事の最後に記した方法です。ただ、判別式を用いて解くことを考えるなら、少なくとも二つの式を用いて2次方程式の形を作ることができる場合においては、”D=0⇔それらが接する”を気にして良い、という風に答えられるかと思います。同値ではないにしても、ほぼ大抵の場合は\(x, y\)が実数かつ\(D=0\)という条件が二つの曲線が接する十分条件になっているはずです。二つの式を用いて2次方程式を作ることができない例というのもたくさんあって、例えば、3次関数と直線のような例があります。このような場合は\(D=0\)を要求する以前に、2次方程式における\(D\)が定義されませんね。
数三という単元まで含めると、2次方程式を作ることができる場合というの以下のようなものがあります。
- 円と直線
- 放物線と直線
- 円と放物線
- 楕円と直線
- 楕円と放物線
- 双曲線と直線
- 双曲線と放物線
- 楕円と双曲線 など
楕円と双曲線は2次曲線という分野で学ぶ関数で、いずれも\(x, y\)の2次式で記述することができます。以上の組み合わせが高校数学で習う有名な2次曲線と、〇〇および△△に入るその組み合わせで、これらのもののうち、片方が直線になっているものはいずれも”D=0⇔それらが接する”という関係が成り立っています。例えば、円と直線が接するという場合。
円と直線の関係は、座標軸に対して平行に移動させても保たれるので、原点を中心とする円\(x^{2}+y^{2}=r^{2}\)と、直線\(ax+by+c=0\ (a, b)\neq (0, 0)\)を考えるだけで十分です。つまり、このときに得られる2次方程式の判別式について、”D=0⇔それらが接するという関係を示せば、一般の円と直線に関して示したことになります。
円と直線が接することは円の中心と直線の距離が半径となることと同値です。ゆえに、円の中心と直線の距離を\(d\)とおくと
$$d = \frac{|c|}{\sqrt{a^{2}+b^{2}}} = r$$
であり、どちらも正の数であるから2乗しても同値性は保たれるので
$$c^{2} = r^{2}(a^{2}+b^{2})$$
より、これが円と直線が接することと同値です。
他方、直線の式を円の式に代入します。
\(b\neq0\)のとき、
$$(a^{2}+b^{2})x^{2}+2acx+c^{2}-b^{2}r^{2}=0$$
であり、\((a, b)\neq (0, 0)\)より、これは2次方程式となります。
このとき、判別式を\(D\)とおくと
$$\frac{D}{4} = b^{2}(a^{2}r^{2}-c^{2}+b^{2}r^{2})$$
となります。ゆえに\(D=0\)と\(a^{2}r^{2}-c^{2}+b^{2}r^{2}=0\)は同値の関係であり、後者は
$$c^{2} = r^{2}(a^{2}+b^{2})$$
より、円と直線が接する条件と同値であることがわかります。
\(a\neq0\)のとき、
$$(a^{2}+b^{2})x^{2}+2bcx+c^{2}-a^{2}r^{2}=0$$
であり、\((a, b)\neq (0, 0)\)より、これは2次方程式となります。同様に判別式を\(D\)として
$$\frac{D}{4} = a^{2}(a^{2}r^{2}-c^{2}+b^{2}r^{2})$$
となります。ゆえに\(D=0\)と\(a^{2}r^{2}-c^{2}+b^{2}r^{2}=0\)は同値の関係であり、後者は
$$c^{2} = r^{2}(a^{2}+b^{2})$$
より、円と直線が接する条件と同値であることがわかります。
このように、いずれの場合でも円と直線の式から2次方程式を作った判別式について\(D=0\)となることは、円と直線が接することと同値であることが示せます。
それ以外のものでも、\(x, y\)が実数かつ\(D=0\)が接するための十分条件にはなっています。これらを覚えておけば、毎回 ”D=0⇔それらが接する”かどうかを調べる必要はなくなると思います。また、例えば円と放物線の式を使って2次方程式を作り、その判別式について\(D=0\)かつ\(x, y\)が実数であることが、「円と放物線が接する十分条件になっている」ということをいちいち証明する必要はないです。このくらいのことは大学受験の知識として解答欄に使っても良いレベルかと思います。だからこそ、チャート式の解答でも断りなく使っているわけですから。ただ、あくまで答えとなるための「十分条件」だということ、また”x, y”が実数であることを確認する必要があること(解答欄にもその確認を書くべき)は忘れてはならないと思います。
後半の質問で反例に気づいていないときや他の問題ではどうすれば良いかということですが、上にあげたパターンの問題の場合なら、直線との組み合わせなら同値として使って良いし、それ以外の組み合わせなら「十分条件」として使って他の場合を考える、という感じで問題には対応できるのではないでしょうか。おそらく数三の知識を使わずに、二つの曲線が接する(共通接線が存在する)問題を議論できるのは、放物線と円、それと直線の組み合わせがほとんどではないでしょうか。それ以外のパターンの問題と遭遇したらぜひ教えてもらいたいです。
もし理系に進む方で、数三の知識を使うことができるようになったら、共通接線の問題パターンは増えます。というのも、楕円や双曲線、3次関数以上の高次関数や分数関数が参戦するからです。しかし、この段階ではそもそも判別式を使わずに(例えば微分法を用いて)接する条件を議論できるようになるので、もはや”D=0⇔それらが接するという関係を考える必要もなくなります。今の段階では、おそらく上で述べたようなパターンの問題に対応できれば十分かと思います。もし、上のパターンで解けない問題が出てきたら、教えていただけると私にとっても、勉強になるのでぜひお願いいたします。
いかがでしたでしょうか。一つの問題にしては非常に長い記事になってしまいましたが、疑問が少しでも晴れていただければ幸いです。もし、まだご不明なところがあったり、議論の中に誤りなどを発見されたときは遠慮なくご指摘ください。


コメント
2つ目の質問内の「座標がただ一つ決まり、そのが≥を満たすならば、問題の円と放物線は2点で接している」のy≧aを満たすならば、の部分が未だによくわからないのですが、もう少しわかりやすく解説お願いできないでしょうか。
よろしくお願いいたします。
ご質問ありがとうございます。半年遅れの回答になってしまい、大変申し訳ありません。他の方の参考にもなればと思い、回答いたします。y^2+y-a-9=0だけを見ているとy>=aの条件は出てこないのですが、そもそもこの式が出てくるためには、y = x^2 + aとx^2 + y^2 = 9のどちらも成り立っている必要があります。この最初の式を見ると、y = x^2 + aとあり、xが実数である限りy>=aが成り立っていることになります。xが実数であることをひとまず認めておくとすると、この問題を通じて、y>=aが成り立っていなくてはなりません。そのため、2つの式から出てきたy^2+y-a-9=0を議論するときにも、y>=aは常に付き纏うことになります。
このように、二つの式を操作して一つの式にしたとき、(二つの式)と(残った一つの式)は必ずしも同値の関係にはないということがポイントです。同値にするには、残った一つの式に、元々あった二つの式のどちらの式を加えなければなりません。このことは、連立方程式(x+y = 1, x-y = 3)を考えるともっとわかりやすいです。この二つの式から、例えばx = 2という式が出てきますが、言わずもがな、元の連立方程式と、x=2は同値ではないですね。同値なのは、元の連立方程式と、例えば、(x=2かつx+y = 1)という式です。それゆえに、y = -1という答えが出てきて、結果的にもとの連立方程式と、(x=2, y = -1)が同値の関係になり、また、これが答えになるわけです。
対応させると、y^2+y-a-9=0が(x=2), y>=aが(x+y=1)ということになるわけです。ですので、y>=aは必須であるということになりますね。