関数の平行移動といえば、2次関数を学ぶときに初めて出てきます。ある関数をy=f(x)と置いて、その関数をp, qだけ平行移動させたときの関数は
$$y-q = f(x-p)$$
となります。さて、ここで疑問です。
自問
p, qと平行移動させるのに、なぜ式の中ではx = x-p, y=y-qと符号を逆転させるのか。
自答
僕は最初にこれを見たとき、この符号の逆転がなかなか受け入れられませんでした。この後、図形と軌跡という単元を学んだとき、平行移動の公式の導出が軌跡の導出と同じ原理に基づいて行われているのを知って納得しましたが、符号の逆転が意味するところを噛み砕いて理解できた訳ではありません。
数学の公式に、「物理的な意味」を付与するのはナンセンス、というか逆効果になることもあるのですが、ここでは符号の逆転が意味することをもう少し理解したいという衝動に駆られましたので、考察してみたいと思います。
まず、世に溢れ出ている公式の導出も一応やっておきます。
定説
もとの関数をy=f(x), 平行した後の関数上の点を(X, Y)とおく。任意のx, yについて
$$x+p = X, y+q = Y$$
が成り立ちます。
$$x=X-p, y=Y-q$$
となる。よって求める関数は
$$Y-q = f(X-p) \leftrightarrow y-q = f(x-p)$$
この解法は数学的に全く問題ないのでそれで納得すべきなのですが、直観的にはおかしなところがいくつかあります。
- X, Yと置いたのに、最後に結局x, yと戻して良いのか。なら、なぜ平行した後の関数上の点を(X, Y)と置いたのか。
- 結局、符号の逆転の意味がわからない。
世に人が指摘しているのように、これらの疑問はもとの関数上の(x, y)と平行移動した後の関数上の(x, y)を混同しているために起こることですが、そんなことを言われても直観というやつは納得してくれません。そこで、少し違うアプローチをしてみます。
自説
実は、「点の移動レベル」の話なら完全に直観と同じです。上の定説に現れた
$$x+p = X, y+q = Y$$
という変形を見ます。ここでの計算は直観と一致した考え方です。しかし、「関数レベル」の話になると
$$y-q = f(x-p)$$
と符号が逆転します。という訳で、「関数レベル」の符号の逆転について考えます。
平行移動が時間とともに推移した、と考えます。すなわち
- t=t0で関数はy=f(x)であった。
- t=t1で関数はy=f(x)をx軸方向にpだけ平行移動した。
- t=t2で関数はy=f(x)をさらにy軸方向にqだけ平行移動した。
図を書くときに面倒なので、今はp>0, q>0とします。このときそれぞれの時刻で、x, yは区別するべきです。一つの世界に二つの時刻でのx, yが入り乱れるのは気持ち悪いです。それこそ直観に反します。そこで、例えば時刻t=t0のときのx, yをx(t0), y(t0)などと書くことにします。
1の条件から
$$y(t_{0}) = f(x(t_{0}))$$
が成り立ちます。次に、1->2の時間変化を考えます。図を用いると以下です。簡単のため関数を2次関数とします。
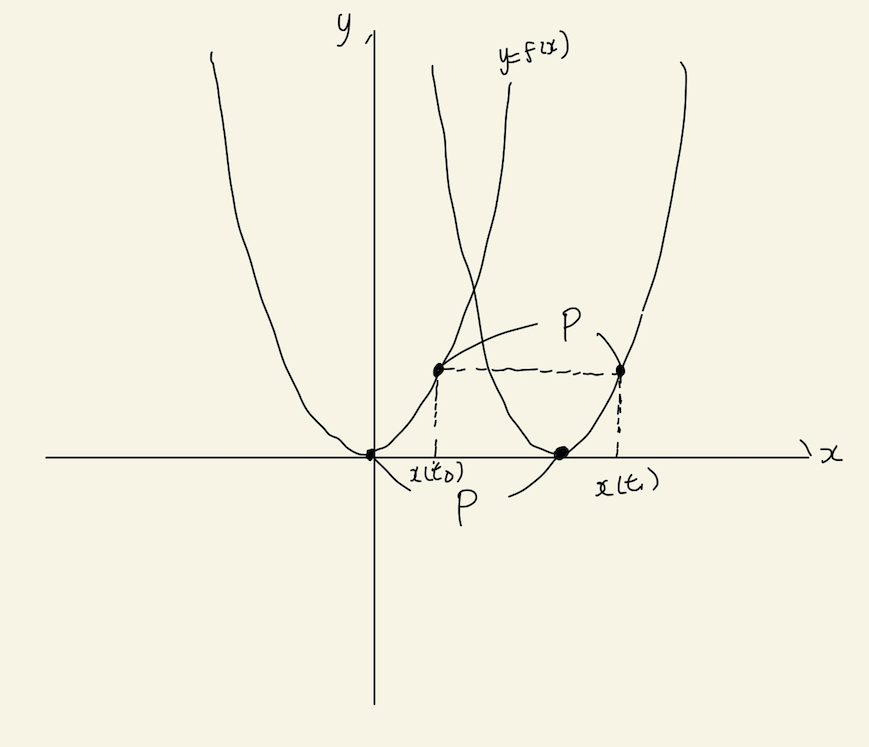
移動後の関数は時刻はt=t1であることに注意して
$$y(t_{1}) = g(x(t_{1}))$$
とかけます。ここで、t=t1の関数をt=t0の関数fで構築することを考えます。移動前の関数と移動後の関数の形は合同なので、t=t1のxに対応するxがt=t0にもあるはずです。よって
$$y(t_{1})=f(x(t_{0}))$$
となります。これでは一つの関数に時刻が二つあるので、時刻をt1にまとめます。そのときにx(t0)とx(t1)の関係を見ると
$$x(t_{1}) = x(t_{0})+p$$
ですから
$$y(t_{1}) = f(x(t_{1})-p)$$
となります。これがt=t1での関数を表します。ここでの-pは、前の時刻の関数で現在の関数を表現している、という意味合いがあるとわかります(前の時刻のことを使っているから負であるという意味)。
次に、t=t2での移動を考えます。
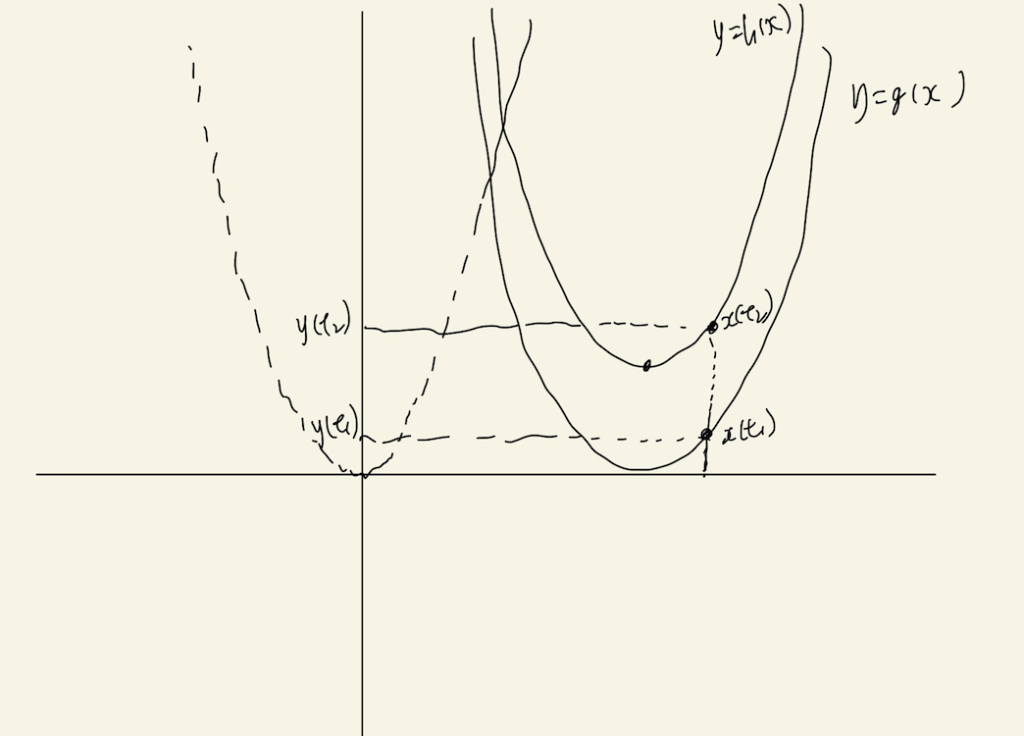
t=t2での移動により、移動後の関数は
$$y(t_{2})=h(x(t_{2}))$$
となります。ここで、先ほどと同じようにt=t1での関数gから関数hを構築します。関数hと関数gでは同じx座標に対して、y座標がqだけずれているので
$$y(t_{2}) = g(x(t_{1}))+q$$
とかけます。ここで、対応するx(t1)とx(t2)は
$$x(t_{1}) = x(t_{2})$$
であることより
$$y(t_{2}) = g(x(t_{2}))+q$$
gの関数形は先ほどすでに求めているので、それを用いて
$$y(t_{2}) = f((x(t_{2})-p))+q$$
です。これでt=t2の関数形も求められました。qも前の時刻の関数から現在の関数を表すことから生じています。
以上のようにして求められたものが
$$y(x) = f(x-p)+q$$
です。これらの符号の意味は、この例では「前の時刻の関数から今の時刻の関数を表現するためのもの」であったことがわかります。時刻をずらすという風に考えれば、なぜX,Yとx,yを区別すべきか、というのも見えてくると思います。
少し方便のような気もしますが、いかがでしょうか。
最後までご覧いただいてありがとうございます。コメントをいただければ幸いです。よろしくお願いします。

コメント