こんにちは、今日はよく眠りました。眠る亀です。
よく眠ったので、その分質問に答えていきたいと思います。よろしくお願いします。
質問
複素数の問題です。n=6 になる理由がわかりません。どなたか解る方いらっしゃったら教えて下さい! 自分は、
ω=1/z=(1+√3 i)/2=cos(π/3)+ i sin(π/3)
ω^n=cos(nπ/3)+ i sin(nπ/3)
迄はしましたが、純虚数になる自然数nが見つかりませんのでこのやり自体が間違っていると思います。

回答
複素数平面の問題ですね。複素数平面は、複素数平面上に図形を書いていくと視覚的に捉えやすくなることが多いです。今回もできる限り図を書いて説明していこうと思います。
まず、点zがたどる軌跡を複素数平面上に書いてみます。
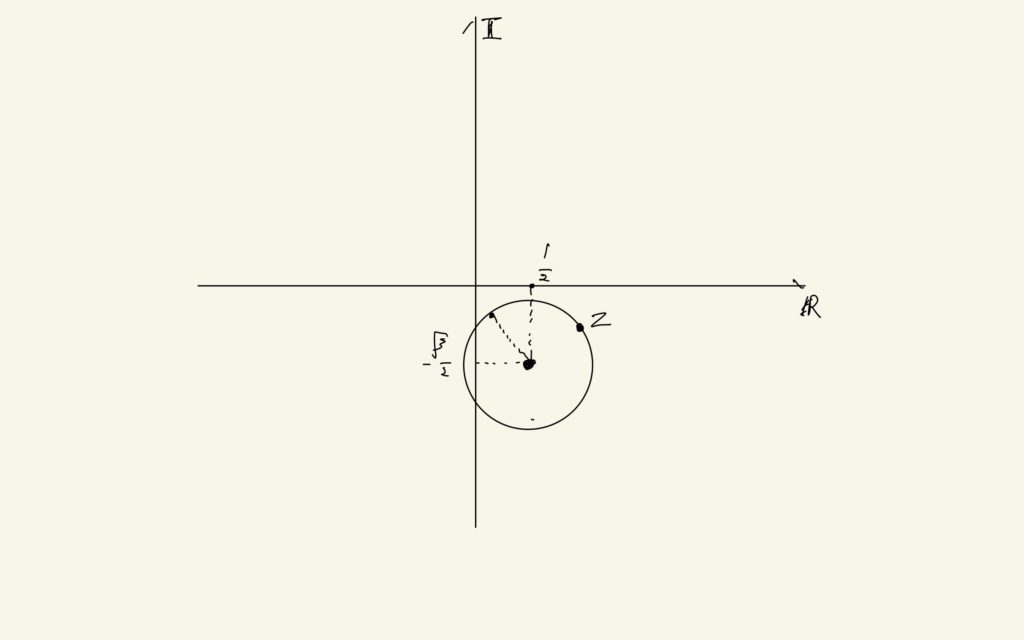
次に、ω=1/zがたどる軌跡を考えます。中心a, 半径rの円上にある複素数zは
$$|z-a|=r$$
を満たすので、今の場合複素数zは
$$\left|z-\frac{1+\sqrt{3}i}{2}\right| = \frac{1}{\sqrt{2}}$$
を満たします。複素数平面の方程式は、ベクトル方程式を求めることと非常によく似ています。というか、そもそも複素数の考え方自体がベクトルの考え方によく似ています。これについては、別の記事で紹介したいと思います。
今、ωの軌跡を求めたいので、z=1/ωとして、zの方程式をωに変えて計算していきます。
$$\left|\frac{1}{\omega}-\frac{1+\sqrt{3}i}{2}\right| = \frac{1}{\sqrt{2}}$$
$$\left|\frac{1}{\omega}-\frac{1+\sqrt{3}i}{2}\right|^{2} = \frac{1}{2}$$
$$\left(\frac{1}{\omega}-\frac{1+\sqrt{3}i}{2}\right)\left(\frac{1}{\overline{\omega}}-\frac{1+\sqrt{3}i}{2}\right) = \frac{1}{2}$$
$$\frac{1}{\omega\overline{\omega}}-\frac{1-\sqrt{3}i}{2\omega}-\frac{1+\sqrt{3}i}{2\omega}+1=\frac{1}{2}$$
$$\frac{1}{\omega\overline{\omega}}-\frac{(1-\sqrt{3}i)\overline{\omega}}{2\omega\overline{\omega}}-\frac{(1+\sqrt{3}i)\omega}{2\omega\overline{\omega}}+\frac{1}{2}=0$$
$$1-\frac{(1-\sqrt{3}i)\overline{\omega}}{2}-\frac{(1+\sqrt{3}i)\omega}{2}+\frac{\omega\overline{\omega}}{2}=0$$
$$\omega\overline{\omega}-(1+\sqrt{3}i)\omega-(1-\sqrt{3}i)\overline{\omega} = -2$$
$$\left(\omega-(1+\sqrt{3}i)\right)\left(\overline{\omega}-(1-sqrt{3}i)\right)=2$$
$$|\omega-(1+\sqrt{3}i)| = 2$$
よって、中心1+\sqrt{3}i, 半径√2の円上にωが分布することがわかりました。
そこで、これを複素数平面に書き足します。
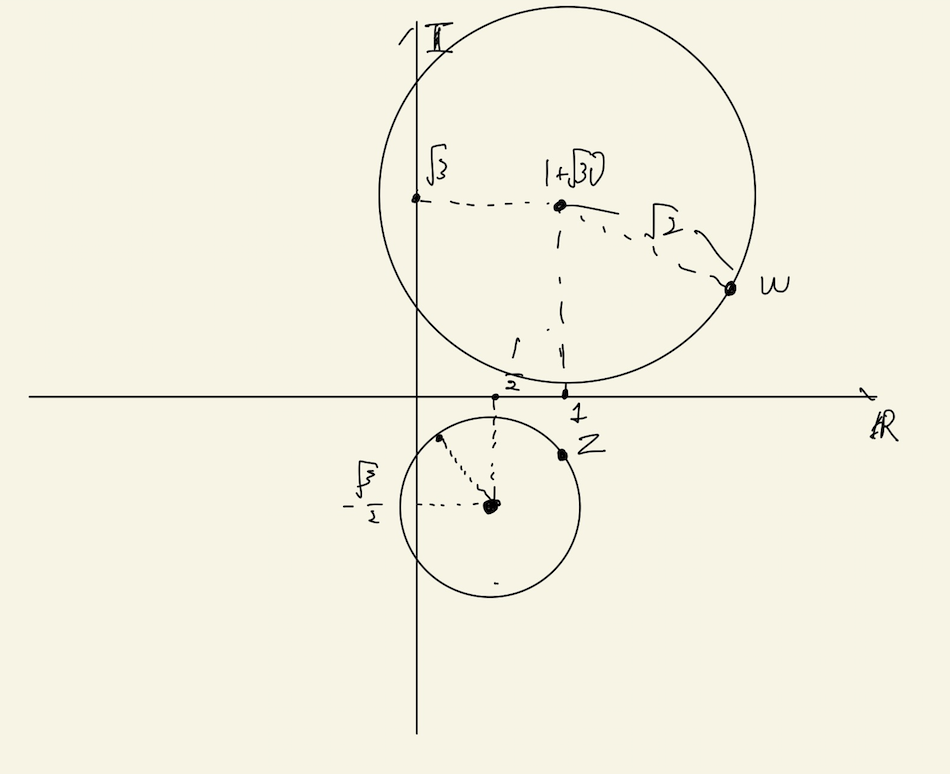
これがωの軌跡です。質問者様は、ここで
$$\omega = \frac{1}{z} = \frac{1+\sqrt{3}i}{2}$$
として計算されていますが、zはそもそも(1+√3i)/2を通らないので、
$$\omega = \frac{1+\sqrt{3}i}{2}$$
と書くことはできません。それで、答えも合わなくなっています。ここまでいくと、あとは幾何的に解けます。ωのうち偏角が最大になるのは、原点からの直線とωの描く円が接するときなので、下の図のような状況です。
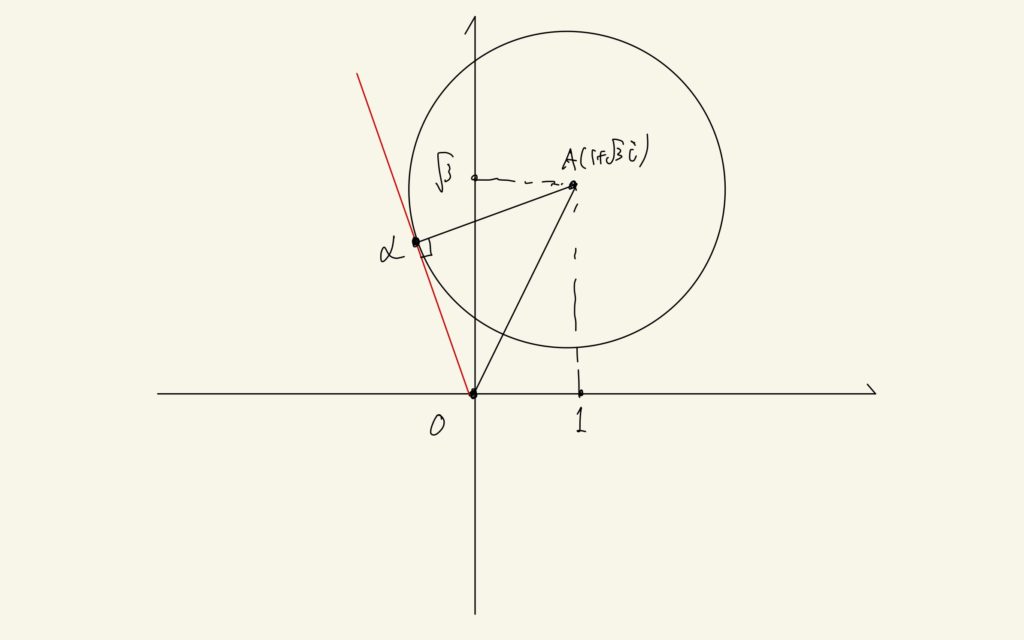
さて、このときの複素数αの偏角を求めます。というのは、実軸とOαのなす角のことです。ωの中心をAとすると△OAαは直角三角形です。さらに、OA=2, Aα=√2であるからOα=√2です。よって、△OAαは直角二等辺三角形であるから∠AOα=π/4です。
また、OAと実軸のなす角、つまり(1+√3i)の偏角はπ/3です。
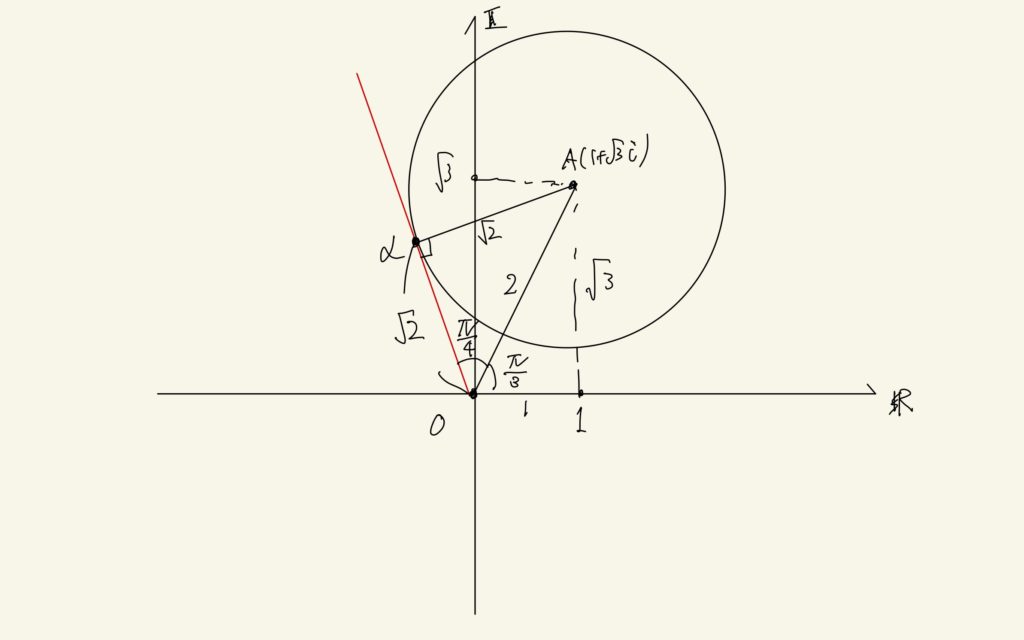
よって求めるαは
$$\alpha = \left( \cos\left( \frac{7\pi}{12} \right) + \sin\left( \frac{7\pi}{12} \right)i \right)$$
です。ゆえにド・モアブルの公式から
$$\alpha^{n} = \left( \cos\left( \frac{7n\pi}{12} \right) + \sin\left( \frac{7n\pi}{12} \right)i \right)$$
となり、これが純虚数となるとき
$$\cos\left( \frac{7n\pi}{12}\right) = 0$$
であるから、これを満たす最小のnは6です。
いかがでしょうか。

コメント