発電機の仕組み（自励式・他励式および直巻・分巻）について考える

先日、発電機の問題に関する質問をいただきました。そこでは、次のような問題が提示されていました。

高校物理では馴染みのない言葉も多いですが、一つ一つの物理量の定義を抑えていくと、理屈としては高校物理の範囲内で十分理解できる問題だと思います。この記事では、発電機の仕組みを考えた上で、上記の問題に取り組んで参りたいと思います。

発電機の理屈

　発電機とは何か、ということを探していると大抵の場合「電磁誘導作用を利用して電気エネルギーを取り出す装置」という説明が見られます。発電機を理解するためには、電磁誘導作用を理解することがもっとも早道であるというわけです。電磁誘導とは、現象的には、コイルと呼ばれる「閉じた回路」を持つ金属線の近くで、磁石を回転させたり動かすことによってコイルに電気エネルギーが発生するという現象です。ファラデーという科学者が発見したため、ファラデーの電磁誘導則とも言います。コイルの近くで磁石を動かすと電気が取り出せるなんて、不思議な現象です。コイルの近くで磁石を動かしたから、なんだというんでしょう。

何が起こっているかを知るためには、磁石の性質に目を向けることが必要です。磁石にはN極とS極があり、砂鉄の実験から、磁石には磁界と呼ばれる目には見えない力の作用が存在しており、我々は磁界の様子を磁力線と呼ばれる曲線を用いて表現します。このことによって、磁石のある付近の空間にはある一定の方向を持った磁力が働いていると考えることができます。もし、コイルの近くで磁石を動かすと、コイルに働く磁力が異なる、すなわちコイルが持つ閉じた回路の中に入る磁力線の数が、その都度異なります。物理学者は、この変化の激しさと発生する起電力に関係があることを突き止めました。電磁誘導は、コイルの中に入る磁力線の数が単位時間あたりに変化する量と、発生する起電力が比例関係にあることを教えてくれています。身近にあるもっともありふれた発電機は、自転車のライトに使われています。あれは、タイヤをこぐ力を部分的に磁石を回す力に使って、それによってライトに仕掛けられたコイルに起電力を発生させ、その電気をライトに使っているという理屈です。

このようにして、運動エネルギーを電気エネルギーに変える装置を発電機と呼んでいます。

発電機の種類

発電機には、大きく分けると直流発電機と交流発電機があります。この記事では主に直流発電機に特化していこうと思います。直流発電機は、磁石を回すための電源の取り付け方によって（*コメントにてご指摘ありました。ここは、磁石の役割を果たす界磁巻線の電源の取り付け方によって、が正しい表現でした。）「自励式」と「他励式」に分けられ、また「自励式」については、回路の組み方によって「直巻式」と「分巻式」およびそれらを複合した「複巻式」に分けられます。「自励式」は、磁石を回すための電圧とその磁石により発電される電機子（発電のためのコイル）を同じ回路に繋ぐ発電方法のことを言います。「他励式」は、電機子の発電とは別に、磁石を回すための電源を用いる発電方法のことです。また用語のつけ方として、「磁石」に使われているコイルを界磁コイル、「発電機」の方に使われているコイルを「電機子コイル」と呼び、それぞれに流れる電流を「界磁電流」や「電機子電流」という用語で区別しています。

「自励式」にはさらに直巻と分巻という区別があり、直巻とは、磁石と電機子を直列につなぐ発電方法のことを指し、分巻とは磁石と電機子を並列につなぐ発電方法のことを指しています。

それぞれの等価回路を次の図に示します。それぞれ他励式発電、自励式発電（直巻・分巻）の順に並んでいます。

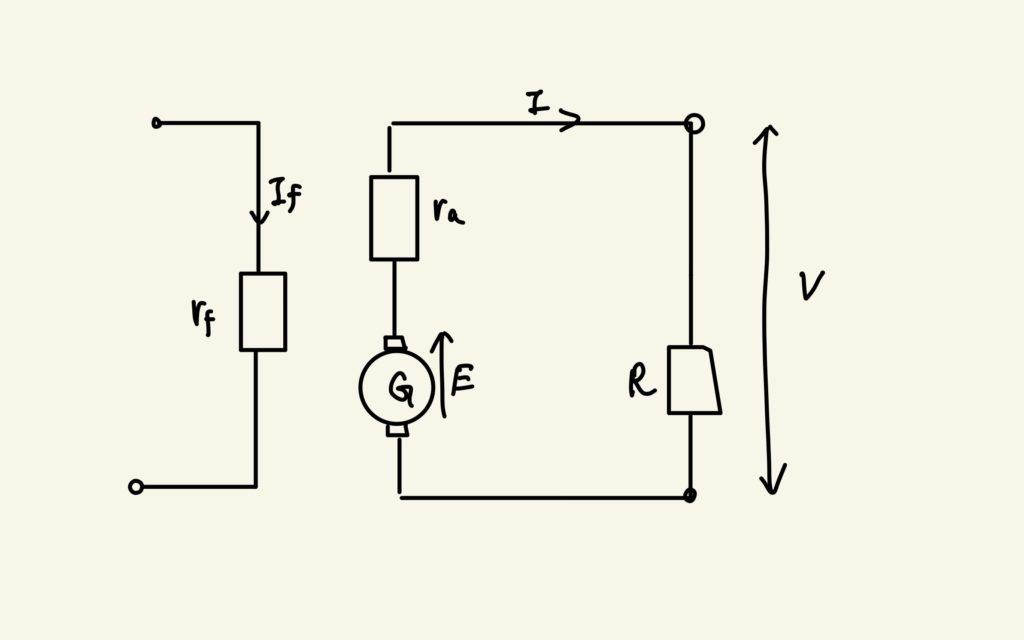
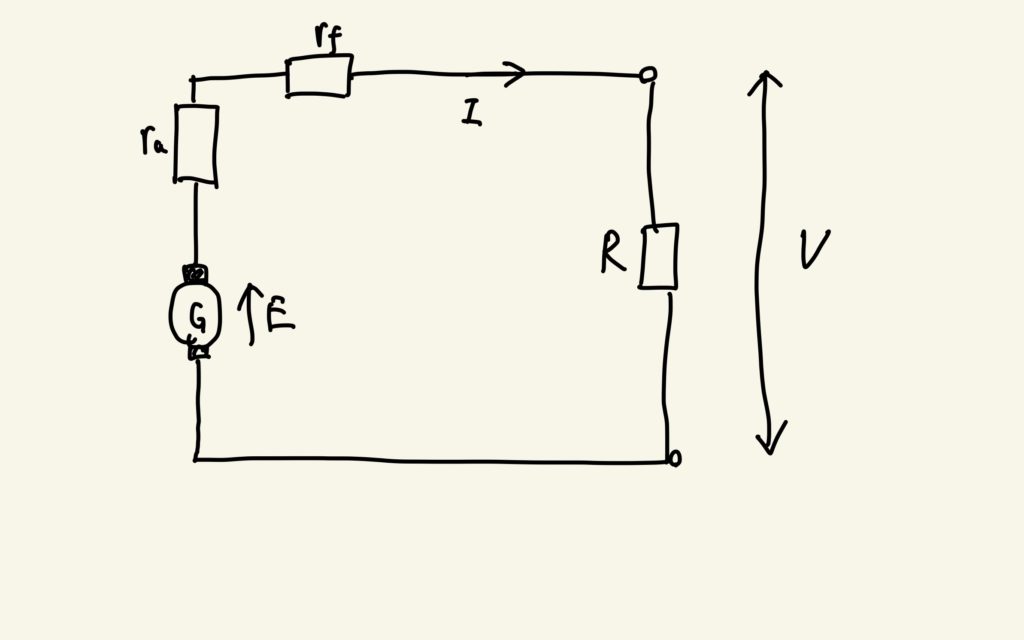
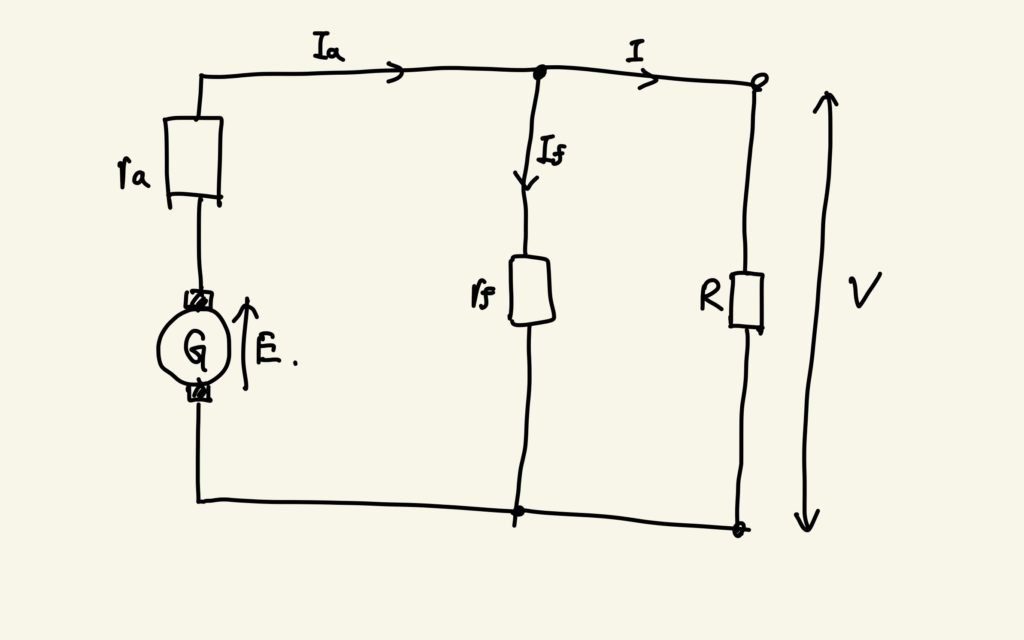
ここで使われている添字についてですが、「f」は磁石すなわち「界磁〜」を指しており、「a」は電機子のことを指しています。すなわち\(I_{f}\)は界磁電流、\(I_{a}\)は電機子電流のことです。また添字のついていない「R」は負荷抵抗器の抵抗を表しており、\(V\)は端子電圧、\(I\)は端子電流のことです。ちなみに「E」は誘導起電力を示しています。

具体的な問題「他励式発電」問題１

ここで「他励式発電」における具体的な問題に取り組みたいと思います。問題は質問していただいたものの1です。

前の項で紹介した等価回路を用いてこの問題に取り組みます。与えられた数値を以下のように等価回路に書き込みます。

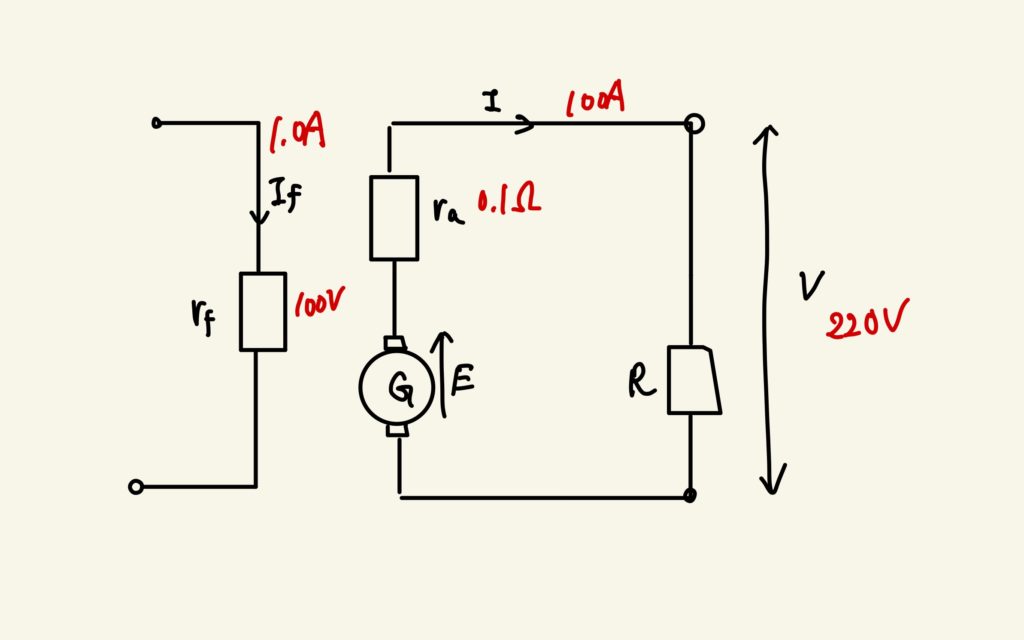
はじめに、求める物理量を確認しておきます。

1. 誘導起電力：図中の\(E\)です。
2. 入力：入力の電力をを指しています。入力の電力はこの後に出てくる出力電力と回路内の損失の和で表せます。回路内の損失には様々なものがありますが、鉄損・機械損・励磁損などがありますが、この問題では題意を考えると電機子抵抗による「鉄損」と界磁抵抗による「銅損」の二つを考慮すれば良いことがわかります。
   ゆえに、入力は「出力」＋「鉄損」＋「銅損」で計算できます。
3. 出力：出力電力のことで、今の場合であれば、\(VI\)を計算すれば良いです。
4. 効率：入力に対する出力の割合で、「出力」から「入力」を割り算します。

以上のように計算を行います。はじめに誘導起電力を求めます。誘導起電力は、電機子が接続されている等価回路について、電機子抵抗と負荷抵抗が直列に接続されていることから電機子での電圧（\(V_{a}\)）と端子電圧\(V\)から求められます。

$$V + V_{a} = E \leftrightarrow E = V+ r_{a}I_{a}$$

よって、\(E = 220 + 10 = 230 \mathrm{V}\)と求められます。
（ここの計算で\(E, V\)を逆にしていました。）

次に出力を求めます。出力は\(VI = 220\times100 = 22000 \mathrm{W}\)です。入力を求めるために電機子での損失と界磁での損失を計算します。それぞれ、\(r_{a}I_{a}^{2}, R_{f}I_{f}^{2}\)で計算できます。ここで、\(R_{f}\)はオームの法則により、\(100/1 = 100 \mathrm{\Omega}\)です。ゆえに、損失の合計を\(L\)と置くと

$$L = r_{a}I_{a}^{2} + R_{f}I_{f}^{2} = 100 + 1000 = 1100 \mathrm{W}$$

と計算できます。以上より入力は\(1100 + 22000 = 23100 \mathrm{W}\)です。

最後に効率(\(e\))を計算します。入力と出力の計算結果より

$$e = \frac{22000}{23100} \times100 \simeq 95.23 $$

よって、問題文に使われている最小の有効数字2桁を用いると95%と計算できます。

具体的な問題「自励式発電（直巻）」問題２

次に自励式発電の中の直巻の問題について考えてみます。問題文は以下です。

問題文の条件を分巻発電機の等価回路に書き込むと以下の図の通りです。

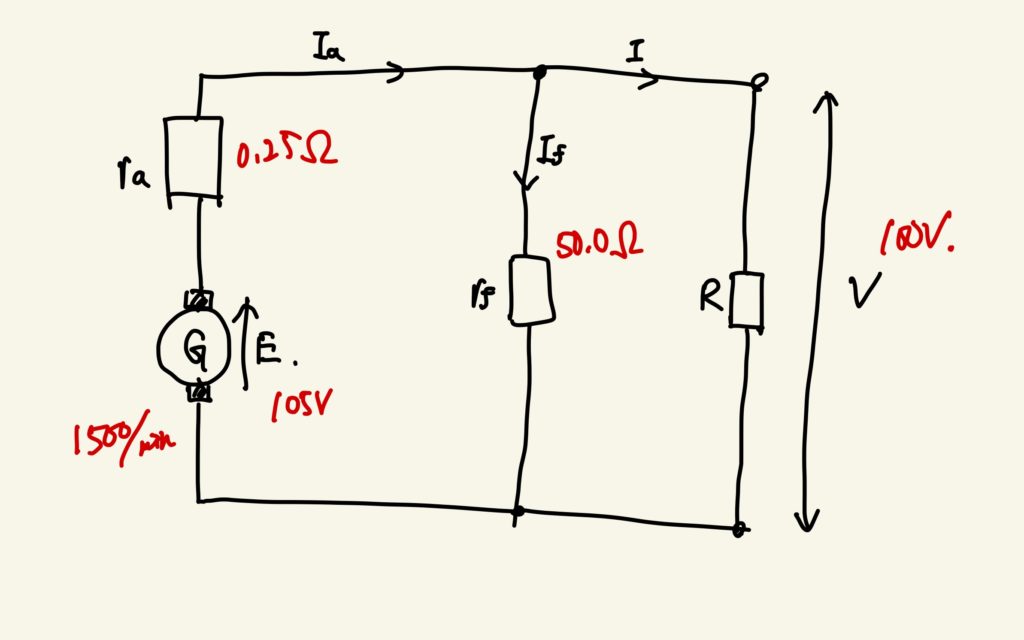
問題文の指定通り、界磁電流と電機子電流、および端子電流を求めます。それぞれ\(I_{f}, I_{a}, I\)を求めることに対応しています。

まず、誘導起電力と端子電圧が与えられていることから、電機子抵抗にかかる電圧を求めることができます。今の場合、電機子抵抗にかかる電圧は\(E-V\)で求められるので、\(105-100 = 5 \mathrm{V}\)です。ゆえに運転中の電機子電流は、オームの法則より\(I_{a} = 5/0.25 = 20 \mathrm{A}\)と計算できます。分巻発電機では、界磁と負荷が並列に接続されていることがわかるので、界磁にも同じく\(100 (\mathrm{V})\)がかかり、界磁電流は\(100/50 = 2 (\mathrm{A})\)とわかります。交流回路に流れる電流の性質から負荷に流れる電流（端子電流）は電機子電流から界磁電流を引けば良いので\(18 \mathrm{A}\)と計算できます。

ちょっと気になりますが、どうやら、回転速度は用いなくても答えが出るようです。

具体的な問題「電圧変動率」問題３

最後に、どのような発電機に対しても同じように定義される物理量である電圧変動率に関する問題を解きます。

電圧変動率は、定格負荷から無負荷に移行したときの電圧変動の割合を表します。すなわち、定格状態において、負荷にかかる電圧を\(V\)とし、無負荷にかかる端子電圧を\(V_{0}\)としたとき、電圧変動率は\(\epsilon\)は

$$\epsilon = \frac{V_{0} – V}{V}$$

と計算でき、通常は\(100\)をかけて単位%で表現します。
（注：電圧変動率の定義で、分母を無負荷の電圧としていましたが、それは間違いで分母は負荷時の電圧です。訂正しました（2020/7/16））。
この定義にしたがって計算すると今の場合電圧変動率は

$$\epsilon = \frac{108-100}{100}\times100 = 8\%$$

と計算できます。

終わりに

私は電気分野の専門家ではないので、もしかすると以上の計算に誤りが含まれている可能性があります。もし、その間違いなどに気づかれた方はぜひ、ご指摘いただけると幸いです。よろしくお願いいたします。