眠る亀です。ゆったりとブログを運営していきたいと思っていますが、出だしはそうも言っていられません。眠らない亀(普通…)として頑張ります。
今回は、積分変数以外の文字のついた式に絶対値の載った定積分の最大値・最小値を求める問題です。絶対値があるので、場合わけの匂いがぷんぷんしますね。
質問
eを自然対数の底とし、0≦x≦eとする。関数
$$f(x) = \int_{0}^{2}|e^{t}-x^{2}|dt$$
について、次の各問いに答えよ。
(1)定積分を計算し、f(x)をxの式で表せ。
(2)f(x)の最大値・最小値を求めよ。また、それらの値をとるときのxの値を求めよ。
回答
絶対値があるときは、絶対値の中身をよく睨み、睨むばかりで埒が明かないときは、絵を描いてみて符号関係を調べるというのが重要です。
(1)
今回は、e^t-x^2について考えます。積分変数はtなので、xは積分の計算の上では「定数」とみなすことができます。積分をするときの変数はtですが、tは0から2まで動きます。xについては, 0≦x≦eという条件があります。このことをもとにして、y=e^{2}, y=x^{2}をy-t平面に描いてみます。注意すべきことは、横軸は”t”なので、xはただの定数であることです。y=x^2だけをみて放物線を思い浮かべないようにします。
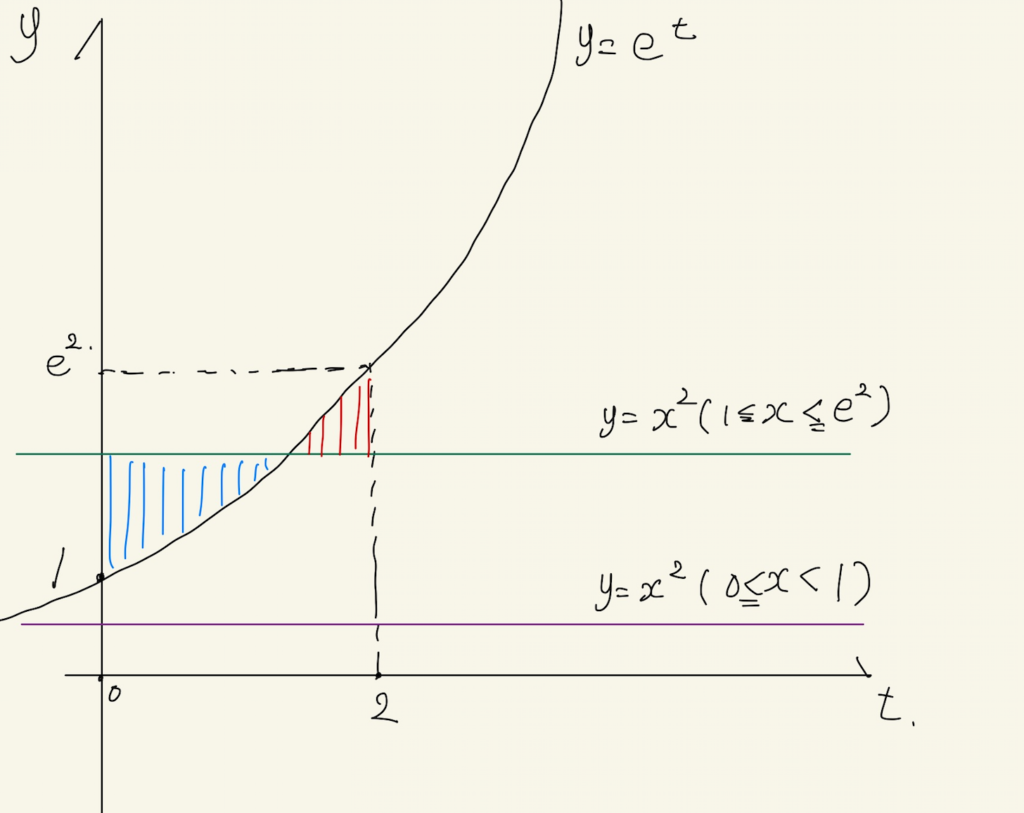
(A)0≦x<1のとき
図の通り、y=e^tは常にy=x^2の上にあります。ゆえに、絶対値の中身は常に正となり、定積分は次のように計算されます。
$$f(x) = \int_{0}^{2}|e^{t}-x^{2}|dt = \int_{0}^{2}(e^{t}-x^{2})dt$$
$$f(x) = [e^{t}-x^{2}t]_{0}^{2} = (e^{2}-2x^{2}) – (1-0) = -2x^{2}+e^{2}-1$$
(B)1≦x≦eのとき
図のように、y=e^tとy=x^2はただ一つの交点を持ちます。この交点のt座標を求めると
$$e^{t} = x^{2} \leftrightarrow t = \log{x^{2}} \leftrightarrow t = 2\log{x}$$
です。よって、0≦t<2logxのときは、絶対値の中身は負。2logx≦t<2のときは絶対値の中身は正となります。このことから、定積分は次のように計算されます。ただし、2logxという形が少しまどろっこしいので、これをαと置いてしまいます。
$$f(x) = \int_{0}^{2}|e^{t}-x^{2}|dt = -\int_{0}^{\alpha}(e^{t}-x^{2})dt+\int_{\alpha}^{2}(e^{t}-x^{2})dt$$
$$\int_{0}^{\alpha}(e^{t}-x^{2})dt = [e^{t}-x^{2}t]_{0}^{\alpha} = e^{\alpha}-\alpha x^{2}-1$$
$$\int_{\alpha}^{2}(e^{t}-x^{2})dt = [e^{t}-x^{2}t]_{\alpha}^{2} = e^{2}-2x^{2}-(e^{\alpha}-\alpha x^{2}) = \alpha x^{2}-2x^{2}+e^{2}-e^{\alpha}$$
$$f(x) = -(e^{\alpha}-\alpha x^{2}-1)+(\alpha x^{2}-2x^{2}+e^{2}-e^{\alpha}) = -2e^{\alpha} +2\alpha x^{2}-2x^{2}+e^{2}+1$$
さて、ここでαを戻してやります。ただし、e^{α}については少し頭を使って戻します。直接に、e^{2\log{x}}と戻すと、途端にごつい形になってしまいます。そうではなくて、そもそもαは次のような式を満たしていました。
$$e^{\alpha} = x^{2}$$
あ、自然と出てきましたね。ということで、心置きなくαを戻します。
$$f(x) = -4x^{2}+4x^{2}\log{x}+e^{2}+1$$
これらの結果をまとめます。
$$f(x) = -2x^{2}+e^{2}-1\ (0\leq x <1),\ f(x) = -4x^{2}+4x^{2}\log{x}+e^{2}+1\ (1\leq x \leq e)$$
(2)
(1)でf(x)の正体を掴んだので、最大値・最小値を求めるには増減表を書き、グラフを書くのが簡便です。
$$f(x) = -2x^{2}+e^{2}-1\ (0\leq x <1)$$
これは、放物線なので微分をするまでもありません。減少関数で、x=0のときe^2-1, x=1のときe^2-3です。
$$f(x) = -4x^{2}+4x^{2}\log{x}+e^{2}+1\ (1\leq x \leq e)$$
これは微分をして、増減表を書きます。微分の計算は以下のように行います。
$$f(x) = -4x^{2}+4x^{2}\log{x}+e^{2}+1$$
$$f'(x) = -8x + 8x\log{x} + 4x = -4x(1-2\log{x})$$
$$f'(x) = 0 \leftrightarrow x=0 または 1-2\log{x} = 0$$
この関数では、1≦x≦eの範囲のみを考えているので、f'(x) = 0となるのは、x = √eのとき。
これをもとに増減表を書きます。
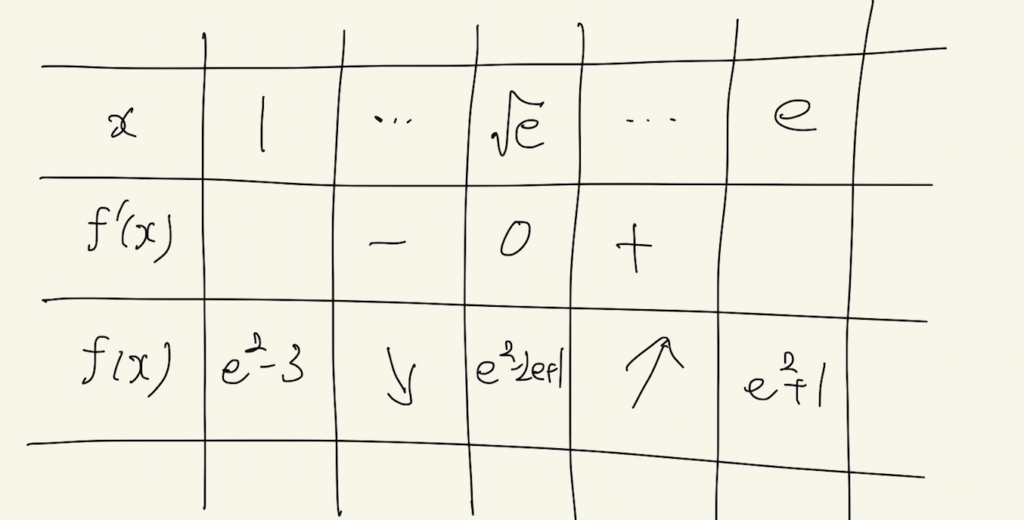
0≦x<1のときも含めてグラフを書きます。
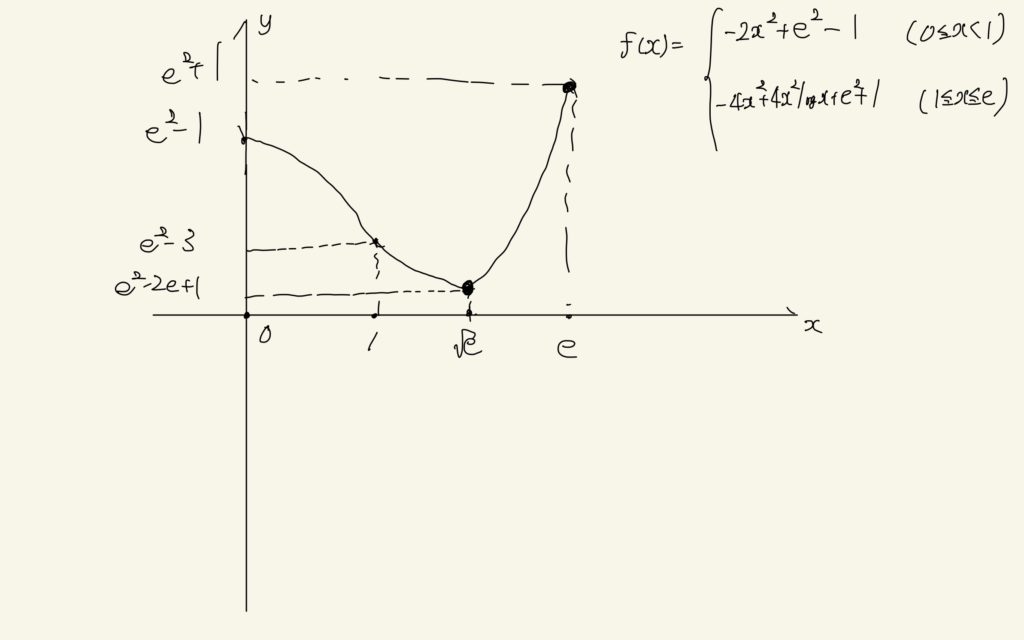
以上より、f(x)の最大値・最小値および、それらの値をとるxの値は
$$\mathrm{min}\ :\ e^{2}-2e+1\ (x=\sqrt{e}) \ \mathrm{max}\ :\ e^{2}+1\ (x=e)$$
いかがでしょうか。

コメント