眠る亀です。よろしくお願いします。今回は、条件式に従う点の軌跡を求める問題に関する質問が挙げられていたので、そちらを解いていきたいと思います。
質問
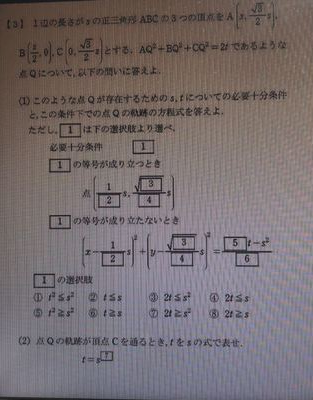
回答
ちょっと面倒ですが、確実な方法をとります。方針は単純で点Qを(X, Y)とおき、AQ^2+BQ^2+CQ^2をX, Yで表し、どのような方程式が出てくるかを見てみます。
(1)
$$\mathrm{AQ}^{2} = (s-X)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}$$
$$\mathrm{BQ}^{2} = \left(\frac{s}{2}-X\right)^{2}+Y^{2}$$
$$\mathrm{CQ}^{2} = X^{2}+\left(\frac{\sqrt{3}}{2}-Y\right)^{2}$$
以上より、AQ^2+BQ^2+CQ^2を求めます。
$$\mathrm{AQ}^{2}+\mathrm{BQ}^{2}+\mathrm{CQ}^{2} = 3X^{2}+3Y^{2}-3sX-2\sqrt{3}sY+\frac{11}{4}s^{2} = 2t$$
s, tは定数なので、この式はX, Yの2次式になっているので円の方程式を表しているように見えます。そこで、X, Yそれぞれについて平方完成を行います。
$$X^{2}+Y^{2}-sX-\frac{2}{3}\sqrt{3}sY+\frac{11}{12}s^{2}-\frac{2}{3}t=0$$
$$\left(X-\frac{s}{2}\right)^{2}+\left(Y-\frac{\sqrt{3}}{3}s\right)^{2}+\frac{1}{3}s^{2}-\frac{2}{3}t=0$$
$$\left(X-\frac{s}{2}\right)^{2}+\left(Y-\frac{\sqrt{3}}{3}s\right)^{2}=-\frac{1}{3}s^{2}+\frac{2}{3}t$$
点Qが存在するというのは、上の方程式を満たすs, tの値が少なくとも一つ存在することを意味する。左辺が0以上であるため、右辺が0以上となることが点Qが存在するための必要十分条件となります。ゆえに以下の式が成り立つことです。
$$-\frac{1}{3}s^{2}+\frac{2}{3}t\geq0$$
$$2t\geq s^{2}$$
このことから、[1] = ⑦
1の等号が成り立つというのは、少し式を遡って
$$\left(X-\frac{s}{2}\right)^{2}+\left(Y-\frac{\sqrt{3}}{3}s\right)^{2}=0$$
となることを意味するので、左辺が0になるときです。そのためには、2乗の中身がともに0になることが必要であり、そのときのX, Yの値は次のように求められます。
$$X=\frac{s}{2}, Y=\frac{\sqrt{3}}{3}s$$
よって、[2] = 2, [3] = 3, [4] = 3
1の等号が成り立たないときというのは、円の方程式をそのまま書けば良いです。
$$\left(X-\frac{s}{2}\right)^{2}+\left(Y-\frac{\sqrt{3}}{3}s\right)^{2}=-\frac{1}{3}s^{2}+\frac{2}{3}t = \frac{2t-s^{2}}{3}$$
よって、[5] : 2, [6] : 3
(2)
点Qが点Cを通るというのは、先ほど求めた軌跡の式に、(0, √3s/2)を代入すれば良いです。
$$\left(0-\frac{s}{2}\right)^{2}+\left(\frac{\sqrt{3}s}{2}-\frac{\sqrt{3}}{3}s\right)^{2}= \frac{2t-s^{2}}{3}$$
$$\frac{s^{2}}{4}+\frac{s^{2}}{12}=\frac{2t-s^{2}}{3}$$
$$t=s^{2}$$
よって、[7] : 2
いかがでしょうか。

コメント