ようこちゃんは、複素数得意なんだっけ?
得意じゃないと思うけど、物理では複素数がなくっちゃ、語れないものがたくさんあるから。苦手意識はないかな。よく「虚数」は「実数」に対して「存在しないもの」という言い方がされることがあるけど、物理では「位相」という形で現実に存在しているものだから、違和感あるな。
存在しないかどうかはともなく、「実数」とはちょっと計算方法が違うよね。だから、今日は複素数と複素平面を総復習しようと思うんだけど、付き合ってよ。
いいよ。今日も面白い問題ばっかりなのかな?
えっへん。それは任せなさい。
別にまみが作ったわけじゃないくせに。
まぁまぁ。じゃあ、まず”複素数”の定義と、その主要な計算方法を確認しておこっか。
複素数の定義とその主要な計算方法
- 複素数とは、\(i^{2} = -1\)となるような虚数単位\(i\)と実数\(a, b\)を用いて
\(z = a+bi\)と記述される数である。\(b=0\)のとき、\(z\)は実数であり、\(a=0\)のとき\(z\)を純虚数という。
\(i^{2}=-1\)とすることで、複素数には実数だけの世界にはない、面白い関係性が見えてくるんだよ。
やっぱり、数学が好きな人の”面白い”って、あまり信用できないんだよね。
え〜? じゃあ、言わせてもらうけど、物理の面白いことって何さ?
物理の面白いところは、う〜ん、アナログのこの世界の複雑な動きを、そうだなぁ、デジタルな数式で簡潔に記述できることかなぁ。
それ、みんなの前で言ってみなよ。大半の人には、理解してもらえないよ。
そうかなぁ。まぁ、数学好きも物理好きも、結局は独りよがりなんじゃない。
そうかなぁ。それはそうと、複素数関連の定義、続けるね。
- 複素数\(z=a+bi\)に対して、\(a\)を複素数\(z\)の実部といい、\(b\)を複素数\(z\)の虚部という。 実部を\(Re(z)\), 虚部を\(Im(z)\)と書くことがある。
- 複素数\(z=a+bi\)に対して、\(\bar{z}=a-bi\)となるものを共役の複素数という。
- 複素数\(z=a+bi\)に対して、\(|z| = \sqrt{a^{2}+b^{2}}\)で定義される\(|z|\)を複素数\(z\)の絶対値と呼ぶ。複素数\(z\)とその共役複素数\(\bar{z}\)との間には次のような関係がある。
$$\frac{z+\bar{z}}{2} = Re(z),\ \frac{z-\bar{z}}{2i} = Im(z)$$
共役と絶対値は、この後の複素平面では幾何的に重要な意味を持ってくるから、心に留めておいてね。
- 実数の軸(実軸)を横軸とし、虚数の軸(虚軸)を縦軸とする。すなわち、ある複素数\(z = a+bi\)において、\(a\)を横軸に\(b\)を縦軸に対応させる。このように複素数を2次元の直交座標系に対応させたものを複素平面(複素数平面)という。
- 複素平面上において、複素数\(z\)の絶対値\(a^{2}+b^{2}\)は原点から複素数までの距離を表す。
- 複素平面上において、複素数\(z\)の共役の複素数\(\bar{z}\)は、実軸に対して対象な点を表す。
- 複素平面上において、原点と複素数\(z\)を結ぶ直線と実軸とのなす角を偏角といい、\(arg(z)\)と書く。
ようこちゃん。3つめのが、なんで成り立つかわかる?
共役の話? \(z = a+bi,\ \bar{z} = a-bi\)だからじゃない?
そうそう。少し迷った時は、複素数は二つの成分に分解して考えてみるとわかりやすいかも。文章で書くとちょっと頭に入りにくいから、図も入れて説明しようかな。
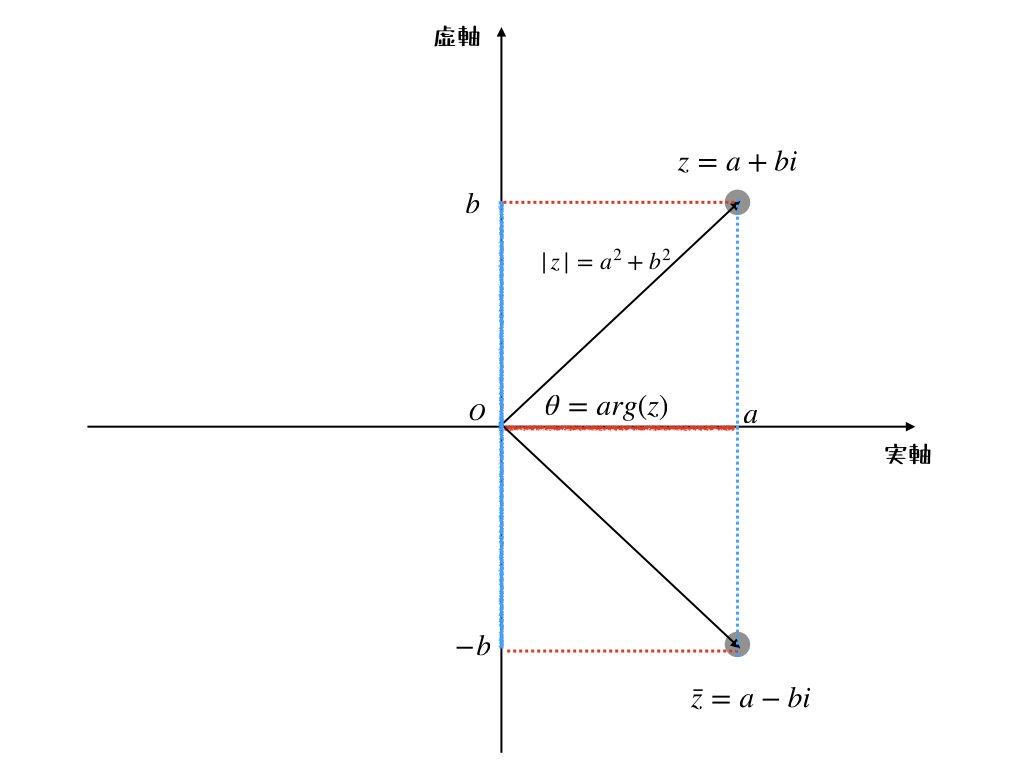
これならわかりやすいね。じゃあ、そろそろ、複素数の計算方法の確認かな?
$$z = r(\cos{\theta}+i\sin{\theta})$$
と書ける。
極形式は、上の図をみながら考えればわかると思う。複素数は、ちょうど三角関数で表せるよね。この式を使って例えば、\(z_{1} = r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}}), z_{2} = r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\)を考えてみよう。それで、ようこちゃん。\(z_{1}\times z_{2}\)を計算してみて。
え……、それ、わたしがやるの?
頼むよ、お願い。
よし、やってやるか。
$$z_{1}\cdot z_{2} = r_{1}r_{2}((\cos{\theta_{1}}\cos{\theta_{2}}+\sin{\theta_{1}}\sin{\theta_{2}})+
i(\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\cos{\theta_{2}}))$$
$$z_{1}\cdot z_{2} = r_{1}r_{2}(\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2}}))$$
上の計算で、
$$z_{1}\cdot z_{2} = r_{1}r_{2}((\cos{\theta_{1}}\cos{\theta_{2}}+\sin{\theta_{1}}\sin{\theta_{2}})+
i(\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\cos{\theta_{2}}))$$
としていた部分は、符号を間違えておりました。コメントにてご指摘をいただきましたので、下記のように修正いたします。
$$z_{1}\cdot z_{2} = r_{1}r_{2}((\cos{\theta_{1}}\cos{\theta_{2}}-\sin{\theta_{1}}\sin{\theta_{2}})+i(\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\cos{\theta_{2}}))$$
ありがとう、ようこちゃん。この計算の結果はとても重要なんだ。つまり、ある複素数\(z_{1}\)に\(z_{2}\)を掛けるってことは、\(z_{1}\)の絶対値に\(z_{2}\)の絶対値を掛けて、\(z_{1}\)の偏角に\(z_{2}\)の偏角を足すことと同じなんだよ。
うんうん。そういう形しているよね。
それで、割り算も似たようなものなんだ。
……割り算はやらないよ。
へへ。まぁ、でも実際に割ってみるとわかりやすいけど、ある複素数\(z_{1}\)を\(z_{2}\)で割るってことは、\(z_{1}\)の絶対値を\(z_{2}\)の絶対値で割って、\(z_{1}\)の偏角から\(z_{2}\)の偏角を引くことと同じだよ。
それは、確かに面白いかも。
でしょ! これが数学の面白さだよ。ようこちゃんもわかってるじゃん。
あ、ありがとう。そういう考え方をすると、ド・モアブルの定理はかなり理解しやすいかも。
$$z^{n} = r^{n}(\cos{n\theta}+\sin{n\theta})$$
が成り立つ。
うん。まさに、この定理を理解するために、ようこちゃんに計算してもらったんだもん。ちゃんと証明するには数学的帰納法が必要だから、ちょっと面倒なんだ。でも、極形式の掛け算・割り算を知っていると、証明しなくても納得しちゃうよね。同じ複素数を\(n\)回掛けるってことは、その偏角\(\theta\)で\(n\)回、回転させて、絶対値\(r\)を\(n\)個掛けるってことと同じだからね。
復習はこのくらいかな? じゃあ、そろそろ問題を見せてよ。
焦らないでよ、ようこちゃん。まだ、偏角についての話とか、正多角形の話とか、色々話したいことあるのに。
それはさ、問題を見ながらその都度教えてもらった方がいいよ。
おっけい! じゃあ、第1問。
2016年 第6問 ”割り算をする覚悟はあるか?”
(イ)\(f(x^{3})\)は\(f(x)\)で割り切れる。
(ロ)\(f(x)\)jの係数\(a, b\)の少なくとも一方は虚数である。
この2つの条件(イ),(ロ)を同時に満たす2次式をすべて求めよ。
まみ……、最初からテーマ重くない? これを最初にやるの?
あ、この問題、知ってた? ようこちゃん解いたことある?
全部は、ないよ。途中まで計算して、挫折しちゃった。
この問題、複素数をテーマにしているけど、全体の99%は実数の計算だから、導入にはちょうどいいと思ったんだけど、ダメかな。
最後まで解ききっていなかったら、まみが一緒にいるし、やってみようかな。
さすが、ようこちゃん! じゃあ、早速だけど、この問題どうやって解く?
う〜ん。\(f(x^{3}) = x^{6}+ax^{3}+b\)が\(f(x) = x^{2}+ax+b\)で割り切れるっているのがポイントだと思うんだけど。
割っちゃおう。
え?
ようこちゃん、面倒なことごちゃごちゃ考えずに、ここでは割っちゃおう。実際、割ってみて、とんでもなく大変な計算だったらやめればいいんだよ。でも、6次式を2次式で割るだけだから、そんな大変じゃないはず。割っちゃえば、あまりは1次式になって、割り切れるという条件を使いやすくなるじゃん。
簡単に言うなぁ。私が挫折したっていうのは、ちょうどその割り算なんだけど。
あたしも一緒にみてるから、もう一度やってみようよ。
わかったよ。じゃあ、やってみよっかな。

できた。何度か間違えて、まみに修正されたけど、最終的にはこんな感じ?
うん。あってるよ。ご苦労様です。これで、割り切れる条件が使えるね。
2. \(-a^{4}b+3a^{2}b^{2}+a^{2}b-b^{3}+b=0\)
割り算よりはましだけど、まだクラクラするなぁ。
””式変形、迷ったら因数分解””
ていう言葉があるよ。試しに因数分解してみたら?
そうだなぁ。じゃあ、1の式を因数分解してみよう。
\(-a^{5}+4a^{3}b+a^{3}-3ab^{2}-ab=0\)
\(-a(a^{4}-4a^{2}b-a^{2}+3b^{2}+b)=0\)
\(-a(a^{4}+(-4b-1)a^{2}+b(3b+1))=0\)
\(-a(a^{2}-b)(a^{2}-(3b+1))\)
あ! 因数分解できちゃった。
そうなんだよ! これがナイスなところだよね。これで因数分解できなかったら、あの割り算が報われないもんね。
え、じゃあ、2の方もできるのかな。
\(-b(a^{4}-3a^{2}b-a^{2}+b^{2}-1)\)
\(-b(a^{4}+(-3b-1)a^{2}+(b-1)(b+1))\)
う〜ん、できそうだけど、できないかな。
わかりやすい形にはならないね。でも、1の式が因数分解できただけで十分だよ。これで、\(a, b\)の関係性がわかるからね。それを2の式に代入すればいいんだよ。
そっか。1の式の因数分解から、
1. \(a=0\)
2. \(a^{2}-b = 0\)
3. \(a^{2}-3b-1=0\)
のいずれかが成り立てばいいんだもんね。じゃあ、1個ずつ試してみようか。
あ、ようこちゃん、計算する?
うん。こないだのリベンジだし、私が計算してもいい?
1. \(a=0\)のとき
このとき、\(b^{2}-1=0\)から\(b=\pm 1\)となって条件(b)、\(a, b\)のいずれか1つが虚数という条件に合わないから不適。
2. \(a^{2}=b\)のとき
このとき、\(b^{2}+b+1=0\)となって、\(b = \frac{-1\pm \sqrt{3}i}{2}\)だから、虚数だね。これはOK。
3. \(a^{2}=3b+1\)のとき
このとき、\(b^{2}=1\)となって、\(b=\pm1\)。\(a\)が虚数にならないといけないから、\(b=-1\)と選んで、\(a^{2}=-2\)より\(a=\pm \sqrt{2}i\)。
うん。いい感じ。でも、2で\(a\)を求めるとどうなる?
う〜ん。そこだよね。
$$a^{2} = \frac{-1\pm \sqrt{3}i}{2}$$
をどうやって解こうかな?
やり方はいくつかあると思うよ。例えば、二重根号を外す方法でも解くことができるけど、今日は、せっかく複素数の復習をしたんだし、ド・モアブルの定理を使うことを考えようよ。
ド・モアブルの定理? え〜と、まずこれを極形式に直すってことかな?
$$a^{2} = \cos{\frac{2}{3}\pi}+i\sin{\frac{2}{3}\pi}$$
これは符号がプラスの場合。もし符号がマイナスなら
$$a^{2} = \cos{\frac{4}{3}\pi}+i\sin{\frac{4}{3}\pi}$$
かな。あ、そうか。ちょうどいい感じの角度になっているんだ。
そこがまた、面白いところだよ。詳しくは最後に言うとして、これで\(a\)の値が求められるよね?
そうだね。絶対値は1だから\(a = \cos{\theta}+i\sin{\theta}\)と置いて、\(0\leq\theta<2\pi\)としよう。すると\(a^{2} = \cos{2\theta}+i\sin{2\theta}\)になるね。\(0\leq 2\theta<4\pi\)だから
1. \(2\theta=\frac{2}{3}\pi, \frac{8}{3}\pi\)と
2. \(2\theta=\frac{4}{3}\pi, \frac{10}{3}\pi\)
のどれでもOKだね。そうすると、
$$a = \cos{\frac{1}{3}\pi}+i\sin{\frac{1}{3}\pi}, \cos{\frac{4}{3}\pi}+i\sin{\frac{4}{3}\pi}$$
$$a = \cos{\frac{2}{3}\pi}+i\sin{\frac{2}{3}\pi}, \cos{\frac{5}{3}\pi}+i\sin{\frac{5}{3}\pi}$$
と書けるから、これを最後、値に戻すと
1. \(b = \frac{-1+\sqrt{3}i}{2}\)のとき、
$$a = \frac{1+\sqrt{3}i}{2}, \frac{-1-\sqrt{3}i}{2}$$
2. \(b = \frac{-1-\sqrt{3}i}{2}\)のとき、
$$a = \frac{-1+\sqrt{3}i}{2}, \frac{1-\sqrt{3}i}{2}$$
だね。
いいね、いいね。じゃあ、最終的に求める答えは?
全部で6個あるね。
$$f(x) = x^{2} \pm \sqrt{2}i -1$$
$$f(x) = x^{2} \pm \frac{1+\sqrt{3}i}{2} + \frac{-1+\sqrt{3}i}{2}$$
$$f(x) = x^{2} \pm \frac{-1+\sqrt{3}i}{2} + \frac{-1-\sqrt{3}i}{2}$$
かな。
うん。正解。どう? 面白かったでしょ。
う〜ん。大変だったけど、なんか、この前やった2012年の第6問の漸化式と同じ感覚だったかな。解いている途中で胸が高まるような。
そういう問題が良問だよね。
ところで、途中でまみが言っていたことって何?
ん? なんのことだっけ?
ほら、なんか、最後に詳しく言うとか、言ってたじゃん。
あ、それは、
$$a^{2} = \frac{-1\pm \sqrt{3}i}{2}$$
の解が面白い形をしているっていう話だね。ようこちゃんが計算したように、これを満たすような複素数は4つあって
$$a = \cos{\frac{1}{3}\pi}+i\sin{\frac{1}{3}\pi}, \cos{\frac{4}{3}\pi}+i\sin{\frac{4}{3}\pi}$$
$$a = \cos{\frac{2}{3}\pi}+i\sin{\frac{2}{3}\pi}, \cos{\frac{5}{3}\pi}+i\sin{\frac{5}{3}\pi}$$
だけど、これを複素平面に書いてみようよ。ちょうど、正六角形の頂点になっていることがわかるんだ!
いいよ。ちょっと待ってね。
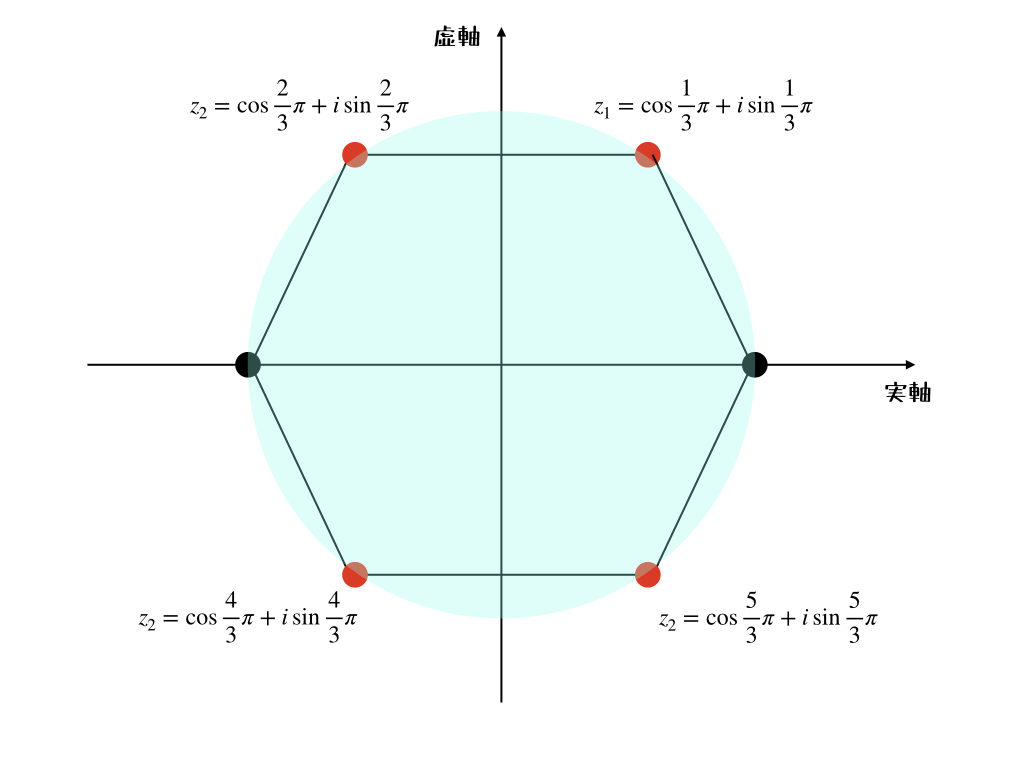
おお、わかりやすい! ちなみに、ようこちゃん。正六角形の頂点を表す複素数を求める方程式は知ってる?
え? う〜んと、なんだろう。
例えば\(z^{6}=1\)だよ。他にも無限にあるんだけど、これが一番簡単かな。これを満たす\(z\)は複素数の範囲で6個あるけど、そのうちの1つが実軸上にあるんだ。今回もそうだよね。じゃあ、これを解いてみよう。
因数分解すればいいのかな?
\(z^{6}-1=0\)
\((z^{3}-1)(z^{3}+1)=0\)
\((z-1)(z^{2}+z+1)(z+1)(z^{2}-z+1)=0\)
だから、\(z = \pm 1, \frac{-1\pm \sqrt{3}i}{2}, \frac{1\pm \sqrt{3}{i}}{2}\)
だよね。そういえば、\(z^{2}+z+1=0\)って、上の問題でも登場したよね。しかも\(z=\pm 1\)以外の4つは上の複素数の問題と一緒だ。
そうなんだよ。さすがようこちゃん。鋭い。ポイントとしては、
\(z^{n}=C\)(\(n\)は自然数, \(C\)は定数)みたいな形があったら、複素平面上正\(n\)角形を思い浮かべることかな。それも中心が原点に一致するような、ね。
なるほど!
じゃあ、今度はそれに関係した問題を解いてみよっか。
2005年前期 第3問 綺麗な対称式が織りなす三角形
対称式を使った式が2つあるね。
1. \(\alpha+\beta+\gamma=0\)
2. \(\alpha^{2}+\beta^{2}+\gamma^{2}=0\)
ようこちゃん、ここから何を連想する?
う〜ん。なんだろう。最初に思い浮かんだのは、
$$(\alpha+\beta+\gamma)^{2} = \alpha^{2}+\beta^{2}+\gamma^{2}+2(\alpha\beta+\alpha\gamma
+\beta\gamma)$$かな。条件を使うと、
\(\alpha\beta+\alpha\gamma+\beta\gamma=0\)になるけど、あんまり関係ないよね。
いやいや、とっても重要! じゃあこれで3つの式ができたね。
1. \(\alpha+\beta+\gamma=0\)
2. \(\alpha^{2}+\beta^{2}+\gamma^{2}=0\)
3. \(\alpha\beta+\alpha\gamma+\beta\gamma=0\)
さぁ、これらの式をじっくりみて、何か思い浮かぶかな? 特に重要なのは1と、ようこちゃんが導いた3だね。
1と3かぁ。何かな。
じゃあ、ヒント。もし、ここに\(\alpha\beta\gamma = 1\)みたいな式が追加されたら、どう?
あ、それなら3次式の解と係数の関係かな?
例えば、\(x^{3}+ax^{2}+bx+c = 0\)という3次方程式の解を\(\alpha, \beta, \gamma\)とすると、
\(\alpha+\beta+\gamma = -a, \alpha\beta+\alpha\gamma+\beta\gamma = b, \alpha\beta\gamma=-c\)だから、\(a=0, b=0, c=-\alpha\beta\gamma\)なのか! もし、\(c=-1\)だとすると
$$x^{3} = 1$$
の解が\(\alpha, \beta, \gamma\)になるから、まみがさっき言っていたように、これらは、1点が実軸上にある正三角形になるんだね。
そうそう。じゃあ、実際のところ\(\alpha\beta\gamma\)はどんな値になるかな?
あ、それはできそう。
\(\alpha\beta\gamma = \alpha(-\alpha\beta-\alpha\gamma)\)
\(=-\alpha^{2}(\beta+\gamma) = \alpha^{3}\)
だね。これを使うと3点が満たす式は
\(x^{3} = \alpha^{3}\)
だ。\(\alpha\)も定数なんだから、やっぱり、正三角形じゃない?
うん。そうだよ。ただ、解答するときは、「外心が原点に一致する正三角形」と言った方がいいと思うな。ちなみに、\(x^{3} = \alpha^{3}\)を解くと
$$x = \alpha, \frac{\alpha\pm\sqrt{3}i}{2}$$
で\(x=\alpha\)以外の解は極形式で書くと
$$x = \alpha(\cos{\frac{2}{3}\pi}+i\sin{\frac{2}{3}}pi)$$
$$x = \alpha(\cos{\frac{4}{3}\pi}+i\sin{\frac{4}{3}}pi)$$
だから、ちょうど、\(\alpha\)という複素数を絶対値は変えずに、\(120^{\circ}\)回転したものと\(240^{\circ}\)回転したものになっているね。だから、確かに正三角形だよ。
うん、スッキリした。
複素数では、こんな風に極形式と回転の考え方でイメージしやすくすると問題が解きやすくなると思うよ。そこで、こんな問題はどうだろう?
1999年前期 第4問 複素平面の上を初等幾何を使って歩く
1. △ABCは辺の長さ\(\sqrt{3}\)の正三角形である。
2. \(\alpha+\beta+\gamma = 3\)
3. \(\alpha\beta\gamma\)は絶対値1で、虚数部分は正
このとき、次の問に答えよ。
(1) \(z=\alpha-1\)とおいて、\(\beta\)と\(\gamma\)を\(z\)を使って表せ。
(2) \(\alpha, \beta, \gamma\)の偏角を求めよ。ただし、\(0^{\circ}\leq arg\alpha \leq arg\beta \leq arg \gamma < 360^{\circ}\)とする。
1, 2で与えられている値がまた絶妙なんだよね。かなり解きやすくしてくれているよ。
問題文がごちゃごちゃしているように見えるけど、こういうのは、実数の時と同じく絵を書いてみるのが一番かな。
ようこちゃん、絵を描く前に確認しておきたいことがあるよ。2番目の条件の意味、どういうことかわかる?
意味? 全ての複素数を足したら、3ということでしょ。
いや、そうだけど。意味っていうか、どんなことがわかるか、っていうか。例えば、こういう形にしたら?
$$\frac{\alpha+\beta+\gamma}{3} = 1$$
あ、複素数平面上の三角形の重心が1ってこと?
そうだよ。全部の複素数を足して3で割った値は複素数平面上の三角形の重心を意味するんだったよね。それで、今回の三角形は正三角形だから、特に重心と外心も一致するよね。複素数は回転ととても相性がいいから、外心がわかっているというのは強力だよ。
OK! じゃあ、それも考慮に入れて描いてみるね。
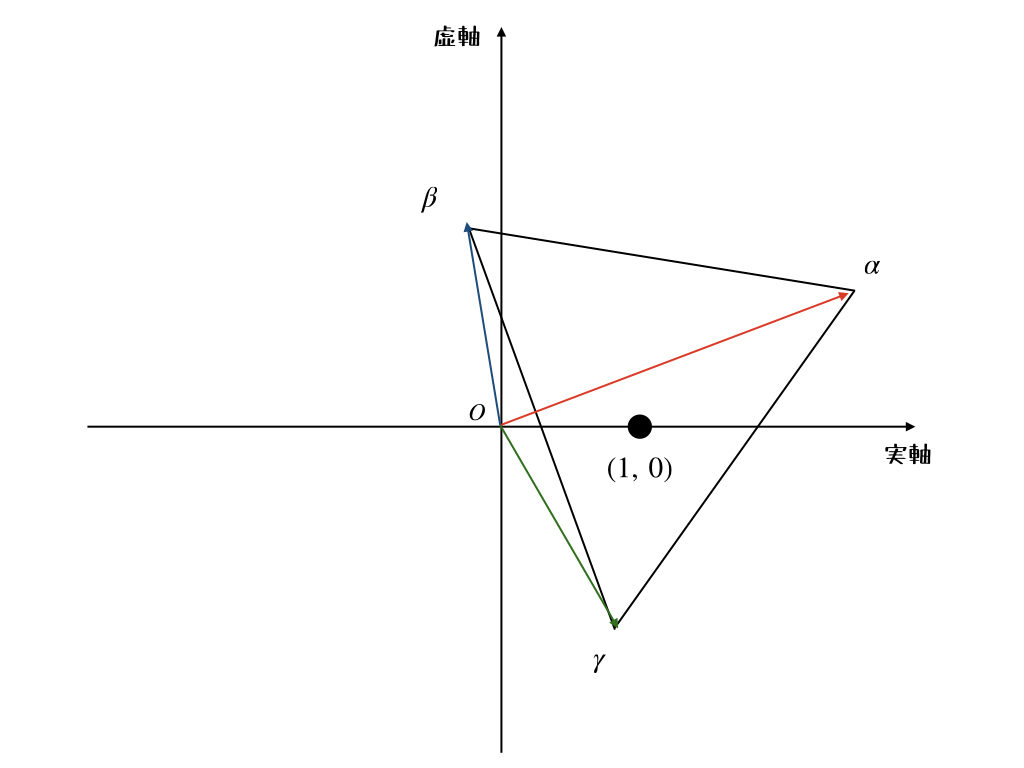
うんうん。じゃあ、1番目の条件を使ってこの三角形の外心の半径を求めるとどうなる?
一辺が\(\sqrt{3}\)だから、正弦定理を使うと
\(\frac{\sqrt{3}}{\sin{60^{\circ}}} = 2=2R\)
だから、1だね。
そう! つまり、(1, 0)を中心に複素数を回転させるときは、大きさを1として考えていいってことなんだよ。これはとても親切だと思うんだよ。
正三角形だから、\(\alpha\)を(1, 0)を中心に\(120^{\circ}\)回転させれば\(\beta\)になるし、\(\alpha\)を(1, 0)を中心に\(240^{\circ}\)回転させれば\(\gamma\)になるし、ってことだね。回転は、それに対応する、大きさ1の複素数をかければいいんだね。
うん。ド・モアブルの定理のとこでやったけど、大きさが1で回転角が\(\theta\)だったら、
$$z = \cos{\theta}+i\sin{\theta}$$
をかけてあげればいいね。
じゃあ、計算してみよっか。
問題は\(\beta, \gamma\)を\(z=\alpha-1\)で表せって問題だけど、これもかなりヒントをくれているよね。
そうだね。回転を考えるときは、回転中心が原点に来るようにみんなを平行移動させてから計算をするのが効率的だからね。\(z=\alpha-1\)で1を引いているのは、\(\alpha\)を-1だけ平行移動させた形を表しているんだね。
つまり、こういうことだよね。
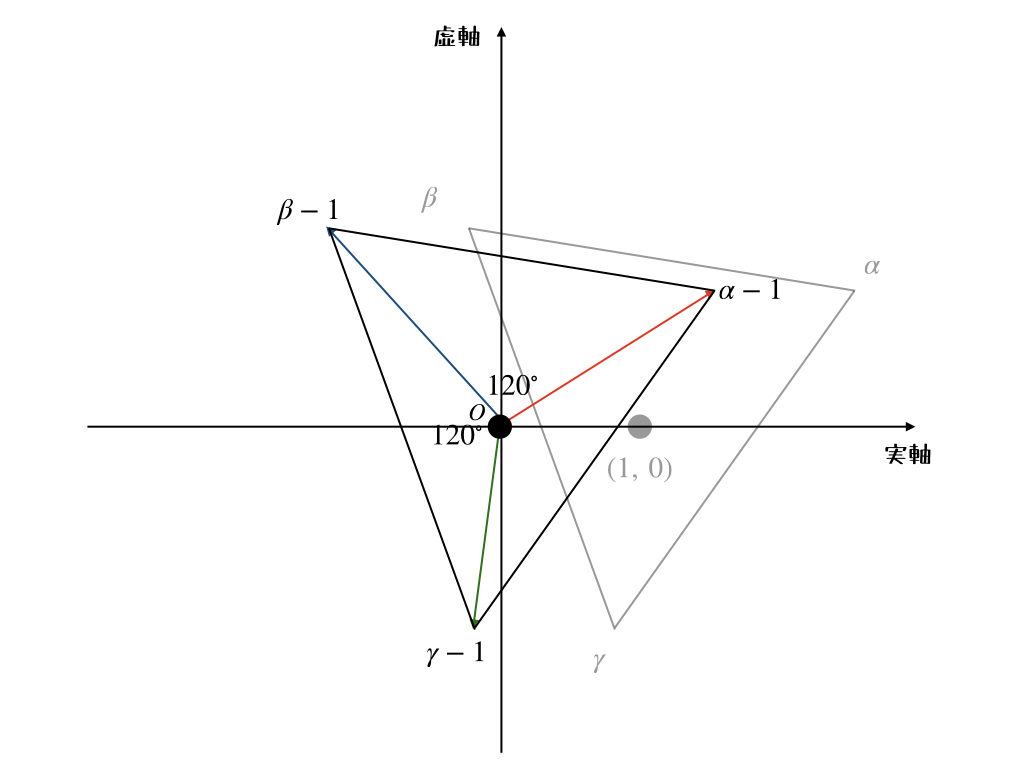
こうやって平行移動させて、\(120^{\circ}\)回転を表す複素数をかけてあげればいいんだ。
1) \(\beta-1\)について
$$\beta-1 = (\alpha-1)(\cos{120^{\circ}}+i\sin{120^{\circ}})$$
$$\beta = 1+z\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right) $$
2)\(\gamma-1\)について
$$\gamma-1 = (\alpha-1)(\cos{240^{\circ}}+\sin{240^{\circ}}i)$$
$$\gamma = 1+z\left(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\right) $$
かな。
うん、バッチリ。あとはこれを使って最後の条件\(|\alpha\beta\gamma|=1\)を計算すればいいね。京大の問題にしては珍しく、すごく綺麗な誘導になっているよ。
よし、じゃあ計算するか。
\(\alpha\beta\gamma = (z+1)\left(1+\left( -\frac{1}{2}+\frac{\sqrt{3}}{2}i \right)z\right)\left(1+\left( -\frac{1}{2}-\frac{\sqrt{3}}{2}i \right)z\right) \)
\(\alpha\beta\gamma = (z+1)(z^{2}-z+1) = z^{3}+1\)
だから
\(|z^{3}+1| = 1\)になればいいんだね。もし\(z\)が実数だったら\(z=0\)だけど、この場合は複素数だから、0とは限らないね。
さて、じゃあ、どうやって解く?
この問題は、偏角を求めることがゴールなんだから、角度に関する情報が欲しいな。例えば\(z\)の偏角っていうのは、\(\alpha-1\)の偏角だから、原点から\(\alpha-1\)を結んだ直線と実軸との角度を意味してるよね。これを求めれば、なんかうまく行きそうな気がするけど。
その感覚素敵。闇雲に計算するんじゃなくって、一度立ち止まってゴールを見直すのが、「完答」するポイントだよ。じゃあ\(z\)の偏角を求めたいよね。
それなら、\(z = \cos{\theta}+i\sin{\theta}\)とおいてみよっか。これを代入して計算すると、ド・モアブルの定理が使えるから
\(|1+\cos{3\theta} + i\sin{3\theta}| = 1\)
になって、あとは絶対値の定義に戻って実部と虚部の2乗をそれぞれ足そう。
$$(\cos{3\theta}+1)^{2} + \sin^{2}{3\theta} = 1$$
$$2\cos{3\theta} = -1$$
$$\cos{3\theta} = -\frac{1}{2}$$
だね。そうすると\(3\theta\)は、\(120^{\circ}, 480^{\circ}, 720^{\circ}\)みたいになっていくけど、\(\gamma\)が\(360^{\circ}\)を超えないのは、\(3\theta = 120^{\circ}\)のときだけだね。だから、\(z\)の偏角は、\(40^{\circ}\)だ。このとき、ちょうど\(\alpha\beta\gamma\)の虚部は正になっているね。
じゃあ、そろそろラストスパートだ。問題は\(\alpha, \beta, \gamma\)の偏角を求めないといけないってことだけど、どうする?
う〜ん。まずは、絵かな。

\(z\)の偏角というのは、\(\alpha-1\)の偏角のことだから、上の図のように角度が決まってるってことだよね。これで、さらに、何がわかるかな。
ヒント出していい?
だめ、ちょっと待って。そういえば、長さが1になるところがいくつかあるね。それを描くと、、、。

お〜。
これで、二等辺三角形ができたね。なるほど。これなら、\(\alpha\)の偏角は\(20^{\circ}\)ってことになるね。
正解。次、\(\beta\)行ってみよう。
多分同じようにできるんだろうから、長さ1にマーキングしていこうっと。
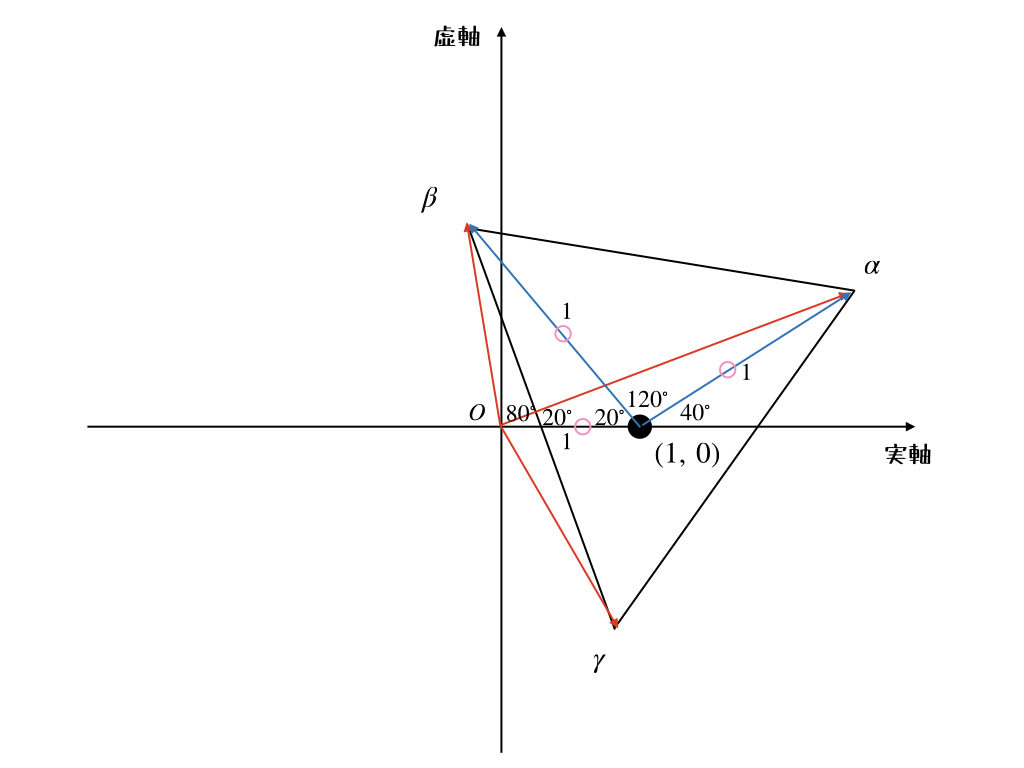
こんな感じでまた二等辺三角形ができるから、\(\beta\)の偏角は\(80^{\circ}\)だね。ちょっと、図が違うけど。
まぁ、よくあることだよね。角度の検討がついていないから、さ。でも、正解は正解。最後は\(\gamma\)だよ。
りょ〜かい。こんな感じかな。
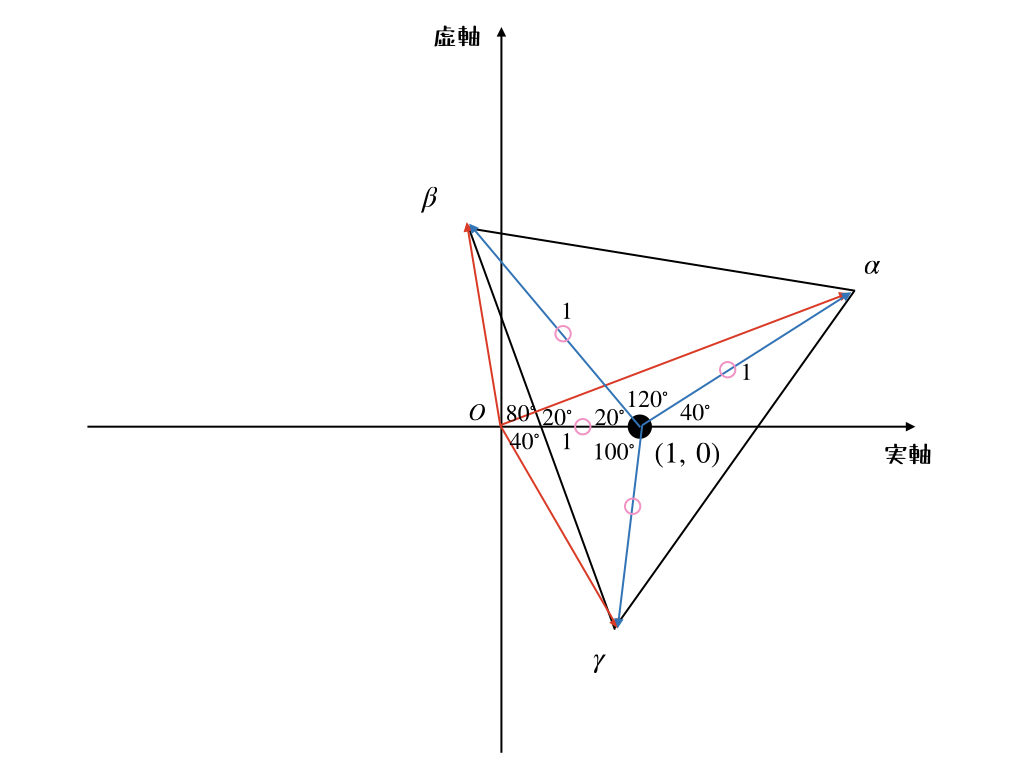
うん、そこは\(40^{\circ}\)だね。そうすると?
\(320^{\circ}\)かな。
うん。完璧だね。こんな感じで、複素平面上を初等幾何の知識を使って歩いていくイメージができると、複素平面にはグッと親近感が湧くんじゃないかな。
確かに、この問題は解いていて、気持ちいいね。
複素数と回転はとても相性がいいのもわかったよね? 一応まとめておくよ。
ってことで、回転系の問題の集大成ということで、こんな問題はどう?
2002年 第6問 どこに向かって回転する?
(ⅰ) \(z_{0} = 0, z_{1} = a\)
(ⅱ) \(n\geq1\)の時、点\(z_{n}-z_{n-1}\)を原点のまわりに\(\theta^{\circ}\)回転すると\(z_{n+1}-z_{n}\)に一致する。
このとき点\(z_{n}(n\geq1)\)が点\(z_{0}\)と一致するような\(n\)が存在するための必要十分条件は\(\theta\)が有理数であることを示せ。
いつもそうだけど、第6問の問題って、パッと見ただけじゃ、何をやったらいいか、全くわからないね。
でも、ようこちゃんのお家芸、”絵を描く”イメージ戦法、があるじゃん。それでなんとなくイメージつかめるかもよ。
まぁ、やってみるよ。
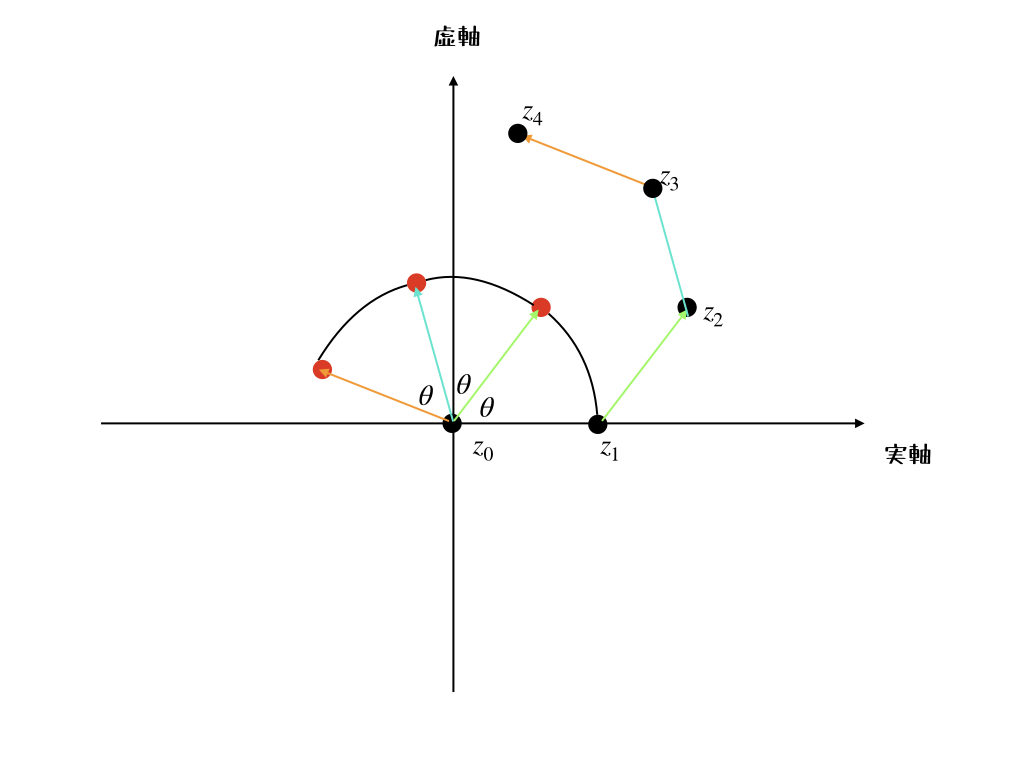
こう? たぶん、原点中心にどんどん回転させていって、その回転した分のベクトル分をどんどん足していくってイメージなんだけど。こんな感じで、複素平面上ではなんとなく、複素数とベクトルが対応するよね。
さすが、ようこちゃん。ナイスイメージだよ。じゃあ、あとは、それぞれのベクトルに対応する複素数の式を求めてみたいね。
それは求めるっていうか、いわゆる回転だよね。今回も回転の際に絶対値が変わらなくて、\(n\)になるまでに0から\(n-1\)回転させたものを足しているから
黒線(\(z_{0}\to z_{1}\)) : \(a\)
緑線(\(z_{1}\to z_{2}\)) : \(a(\cos{\theta^{\circ}}+i\sin{\theta^{\circ}})\)
青線(\(z_{2}\to z_{3}\)) : \(a(\cos{2\theta^{\circ}}+i\sin{2\theta^{\circ}})\)
オレンジ線(\(z_{3}\to z_{4}\)) : \(a(\cos{3\theta^{\circ}}+i\sin{3\theta^{\circ}})\)
だね。で、結局
\(z_{n} = a+a(\cos{\theta^{\circ}}+i\sin{\theta^{\circ}}) + a(\cos{2\theta^{\circ}}+i\sin{2\theta^{\circ}}) +
\cdots\cdots +\)
\(a(\cos{(n-1)\theta^{\circ}}+i\sin{(n-1)\theta^{\circ}})\)
かな。
そうなっているね。わかりやすく回転の複素数を\(z = \cos{\theta^{\circ}} + i\sin{\theta^{\circ}}\)とおくと
$$z_{n} = a(1+z+z^{2}+z^{3}+\cdots\cdots + z^{n-1})$$
と書けるよ。ね〜、これを見ると何かを思い出すよね。
最初の問題に関係しているね。つまり、
$$z_{n} (z-1)= a(z^{n}-1)$$
ということを言いたいのかな?
そうそう!
じゃあ、\(z_{n}=0\)となる\(n\)が存在するって、どういうことだろ?
う〜ん?
まず、\(z_{n}=0\)になるというのは、
\(1+z+z^{2}+\cdots\cdots+z^{n-1}=0\)になることと同じで、、、それで、これが成り立つってことは、\(z^{n}=1\)になるってこと、、だね!
そうだよ。\((z-1)(1+z+z^{2}+\cdots\cdots+z^{n-1}) = z^{n}-1\)だからね。
ということは、\(z_{n}=0\)になるような\(n\)の下では、
$$z^{1}+z^{2}+\cdots\cdots+z^{n-1}+z^{n} = 0$$
が成り立つってことなんだね。
その通り! さぁ、いよいよ\(\theta\)に近づいてきたよ。
あっ、そうか! \(n\)角形の対称性を考えると、\(n\theta=360\)になれば、これって満たされるんだ。だって、正\(n\)角形の重心は、それらの頂点が\(z, z^{1}, z^{2}, \cdots\cdots, z^{n-1}, z^{n}\)と表されているんなら、
$$\frac{z^{1}+z^{2}+\cdots\cdots+z^{n-1}+z^{n}}{n}$$
で、重心と外心が一致して、今は原点を中心とする円上にあるんだから
$$\frac{z^{1}+z^{2}+\cdots\cdots+z^{n-1}+z^{n}}{n} = 0$$
だもん。このとき\(\theta = \frac{360}{n}\)で、有理数になってる!
なるほどなるほど。ようこちゃん、今までやったこと、ちゃんと活かし切ってるね。でもね、あと一歩足りないなぁ。本当にあと一歩なんだけど。
やっぱり? う〜ん、\(n\theta=360\)以外にも条件があるのかな。もしかして、360じゃなくてもいいとか? 720でもいいのかな?
試しに\(\theta\)の制限取っ払って、考えてみたら?
じゃあ、\(n\theta = 720\)で、\(n=6\)の場合を考えるよ。
\(z^{1}, z^{2}, \cdots\cdots, z^{n-1}, z^{n}\)それぞれの偏角の値は\(120^{\circ}, 240^{\circ}, 360^{\circ}, 480^{\circ},600^{\circ}, 720^{\circ}\) で、正三角形の各偏角が2回繰り返されているだけだから、
$$z+z^{1}+z^{2}+\cdots\cdots+z^{n-1}+z^{n} = 0$$
は確かに成り立つね。
そうなんだよ。実は、zの偏角がある\(\theta\)で
$$z^{1}+z^{2}+\cdots\cdots+z^{n-1}+z^{n} = 0$$
となるときは、自然数\(p\)を用いて、\(\theta\times p\)としても成り立つんだよ。ようこちゃん、証明できるかな?
え? 私にやらせるの?
まだ、見当も付いてないよ。
じゃあ、ヒント。偏角を\(p\)倍するってことは、ド・モアブルの言葉でいうとどういうことかな?
え? ド・モアブルの言葉って何?
ド・モアブルの法則で言うと、ってことだよ!
あ、ごめんごめん。え〜と、たとえば\(z=\cos{\theta^{\circ}}+i\sin{\theta^{\circ}}\)を考えたとして、偏角を\(p\)倍すると
\(z^{\prime}=\cos{p\theta^{\circ}}+i\sin{p\theta^{\circ}}\)
だね。え〜と、\(p\)が自然数だから、まさか逆に使う?
そう! 滅多にお目にかからないけど、ド・モアブルの法則を逆に使ってみると?
$$z^{\prime}=\cos{p\theta^{\circ}}+i\sin{p\theta^{\circ}}=(\cos{\theta^{\circ}}+i\sin{\theta^{\circ}})^{p} = z^{p}$$
なの!?
そんなに驚くことないと思うけどなぁ。だって、偏角を\(p\)倍するってことは、回転の回数を\(p\)倍にするってことなんだから。
はいはい、数学ができる人にとっては当然かもね!
まぁ、そんな怒らないでさ、続きを考えようよ。
ってことは、偏角を\(p\)倍したものは
$$z^{p}+z^{2p}+\cdots\cdots+z^{(n-1)p}+z^{np}$$
なんだから、これを等比数列の公式で計算すると
$$z^{\prime} = \frac{1-(z^{p})^{n}}{1-z^{p}} = \frac{1-z^{pn}}{1-z^{p}}$$
だから、\(z^{1}+z^{2}+\cdots\cdots+z^{n-1}+z^{n} = 0\)が成り立っているなら、\(z^{n}=1\)で、当然\(z^{pn}=1\)だから、確かに0だ。すごい!
綺麗に証明できたでしょ。ちなみに、\(\theta\)の制限を考えると、\(p<n\)だから、\(p^{n}=1\)になることはないね。さぁ、ラストスパートだよ。
そうだね。つまり、\(p\)を自然数として
$$n\theta=360\times p$$
となればいいんだから\(\theta\)について書き直すと
$$\theta = \frac{360p}{n}$$
で、分母も分子も整数だから、これは確かに有理数になる。
うん! バッチリ。
ていうか、まみのおかげだけどね。なかなか楽しかったよ。
今まで回転の問題ばっかだったから、最後に複素平面上の円の問題をやろっか。
その前に、簡単でいいから複素平面上の円のことを少し復習しようよ。
りょ〜かい。じゃあ、複素平面上の円の方程式からね。
$$|z-\alpha| = r$$
と書ける。
なんか、ベクトルの円の方程式に似ているよね。
そうなんだよね。これに限らないけど、複素数はベクトルと同じような感覚で考えるとわかりやすいかも。ちなみにベクトルの円の方程式でよく出てくる計算は両辺を2乗して
$$|z-\alpha|^{2} = r^{2}$$
$$(z-\alpha)(\bar{z}-\bar{\alpha})=r^{2}$$
$$z\bar{z}-\alpha\bar{z}-\bar{\alpha}z+\alpha\bar{\alpha} = r^{2}$$
という風にバラす計算だね。
確かに、半径を求めるときとかに、こういう計算をよくする気がする。
じゃあ、問題やってみよ。
2004年 第5問 お前が通るなら俺も!
さぁ、どうする? ようこちゃん。
せっかく復習したのに、半径がわかってないとはね。
ようこちゃん。わかっていないなら出せばいいじゃん。
え? ああ、そうだけど。計算するの?
ちなみに、円\(C\)が1, -1を通るってことは、中心が虚軸上にあるってことはいいよね? だから、中心を表す複素数は\(ik\)と書ける。さぁ、ようこちゃん。がんば!
ん〜と、半径が等しいんだから、\(|ik-\alpha| = |ik+1|\)を解けばいいわけね。これはさっきみたいに2乗すればいいんだね。
\((ik-\alpha)(-ik-\bar{\alpha}) = (ik+1)(-ik+1)\)
\(k(\bar{\alpha}i-\alpha i) = |\alpha|^{2}-1\)
という風に計算できるから
$$ik = \frac{|\alpha|^{2}-1}{\bar{\alpha}-\alpha}$$
かな。
そうだね。ってことで円Cの方程式を求めるには、あと半径が必要だね。
半径、、、か。じゃあ
$$\left|\frac{|\alpha|^{2}-1}{\bar{\alpha}-\alpha}-\alpha\right|$$
を計算するんだね。いいよ、やりましょう。
$$\left|\frac{|\alpha|^{2}-1}{(\bar{\alpha}-\alpha)}-\alpha\right| = \left|\frac{|\alpha|^{2}-|\alpha|^{2}+\alpha^{2}-1}{\bar{\alpha}-\alpha}\right|$$
だから半径\(r\)は
$$r = \left|\frac{\alpha^{2}-1}{\bar{\alpha}-\alpha}\right|$$
だね。結局円Cの方程式は
$$\left|z-\frac{|\alpha|^{2}-1}{\bar{\alpha}-\alpha}\right| = \left|\frac{\alpha^{2}-1}{\bar{\alpha}-\alpha}\right|$$
だね。
ってことで、ようこちゃん、あとは何をすればいい?
わかってるくせに!
左辺に\(-\frac{1}{\bar{\alpha}}\)を代入して右辺と等しいことを確かめればいいんでしょ。
見た目ほどは複雑じゃないから大丈夫だよ。
よし。
$$\left|-\frac{1}{\bar{\alpha}}-\frac{|\alpha|^{2}-1}{(\bar{\alpha}-\alpha)}\right|$$
$$=\left|\frac{-\bar{\alpha}+\alpha-\bar{\alpha}|\alpha|^{2}+\bar{\alpha}}{\bar{\alpha}(\bar{\alpha}-\alpha)}\right|$$
$$\left|\frac{\alpha-\alpha\bar{\alpha}^{2}}{\bar{\alpha}(\bar{\alpha}-\alpha)}\right|$$
$$\left|\frac{\alpha(1-\bar{\alpha}^{2})}{\bar{\alpha}(\bar{\alpha}-\alpha)}\right|$$
これ以上簡単になるかな?
ようこちゃん、そういえば絶対値の性質に
$$|z_{1}z_{2}| = |z_{1}||z_{2}|$$
というのがあるって知ってた?
\(z_{1}=x_{1}+iy_{1}, z_{2} = x_{2}+iy_{2}\)とすれば、証明できるよ。
あ、それいただき。だとすると
$$\left|\frac{\alpha(1-\bar{\alpha}^{2})}{\bar{\alpha}(\bar{\alpha}-\alpha)}\right|$$
はもっと簡単になって
$$\frac{|\alpha|}{|\bar{\alpha}|}\times\left|\frac{1-\bar{\alpha}^{2}}{\bar{\alpha}-\alpha}\right| = \left|\frac{1-\bar{\alpha}^{2}}{\bar{\alpha}-\alpha}\right|$$
になるね。
いよいよ右辺との比較だね。
$$\left|\frac{\alpha^{2}-1}{\bar{\alpha}-\alpha}\right|$$
$$\left|\frac{1-\bar{\alpha}^{2}}{\bar{\alpha}-\alpha}\right|$$
同じ形をしているわけではないけど。
ようこちゃん、グッとにらめば、何か思いつくよ。
睨むの? え〜と。
共役? かな。上の式の共役をとると
$$\frac{\bar{\alpha}^{2}-1}{\alpha-\bar{\alpha}}$$
$$\frac{1-\bar{\alpha}^{2}}{\bar{\alpha}-\alpha}$$
となって、下の式に一致するね。
お見事。共役な2つの複素数は当然大きさは一緒だから、これで、証明できたね。
あ〜。今日も疲れたな。複素数は計算が大変だね。
でも、複素数と回転の関係性はしっかり頭に入れておいたほうがいいよ。他の単元にはなかなか、こういう計算は現れないから。
そうだね! 今日もありがとう、まみ。
いえいえ、どういたしまして。次は何をやろっかな。



コメント
極形式のZ1*Z2の計算の部分の実部の(cosθ1cosθ2+sinθ1sinθ2)ではなく(cosθ1cosθ2-sinθ1sinθ2)だと思います。
黒山様、
ご指摘いただきましてありがとうございます!
その通りでございます。大変失礼致しました。
修正しておきました。
2016.6の問題で、問題文の(イ)の次数がちがうと思います
ご指摘ありがとうございます。
問題文を間違えてしまい、大変申し訳ありません。
修正しておきます。