ねぇ、まみ。不等式の証明方法なんだけどさ、私はいつも(左辺ー右辺)の形を作ることばかり考えているんだけど、たまに相加・相乗平均を使ったり、積分を使ったりするじゃん。どんな方法があるのかまとめて教えてくれない?
不等式の証明かぁ。いろんなタイプがあるからねぇ。全部ひっくるめて教えちゃおう。その代わり、今日もがんがん計算してもらうからね。
わかった、わかった。覚悟しとくよ。
まず、重要な方法を列挙してみるね。私の勝手な感覚で、特に重要なものを上から並べてみるよ。
2. 特別な不等式の活用(特に相加・相乗平均とコーシーシュワルツの不等式)
3. 凸関数の性質
4. 近似の利用
5. 数学的帰納法
1を証明するときには、色々なタイプがあることに注意しないとダメだよ。例えば、\(A>B\)を証明したいときには
1. \(A-B>0\)を示す
2. \(A, B\)が両方とも正なら\(\frac{A}{B}>1\)を示す
3. \(A, B\)が両方とも正なら\(A^{2}-B^{2}>0\)を示す
みたいに、パターンがあるからね。
どの場合でも、\(A-B=f(x)\)みたいにおいて、微分をして最小値や最大値を求めたりすると、証明できることが多いよね。文字が2つある場合でも、1文字ずつ微分をすればできちゃうし。
うん、確かに。それが一番パワーがあると思うよ。でも、そういったことができない、または面倒くさいときには、他の解法を使っていくのがいいと思う。
例えば、相加・相乗平均だね。
$$\frac{a+b}{2}\geq\sqrt{ab}$$
が成り立つ。等号は\(a=b\)のときに成り立つ。
高校の教科書では2文字の場合しか証明していないけど、\(n\)文字の場合でこのような関係が成り立つことが証明されているね。ちなみに、証明ではあまり出てこないけど、最小値や最大値を求めるときにコーシー・シュワルツの不等式も使えることがあるよ。
これも、\(n\)文字の場合に成り立つことが示されているよね。
うん、そうだね。実践的には、3文字,3文字の場合がよく使われる気がするなぁ。
3つめの、凸関数と不等式の関係は、かなり重要だよね。
そうなんだよ。ようこちゃん、この話を一発で理解するような絵をかける?
凸関数の? う〜ん、じゃあやってみる。下に凸な関数だけを考えるよ。
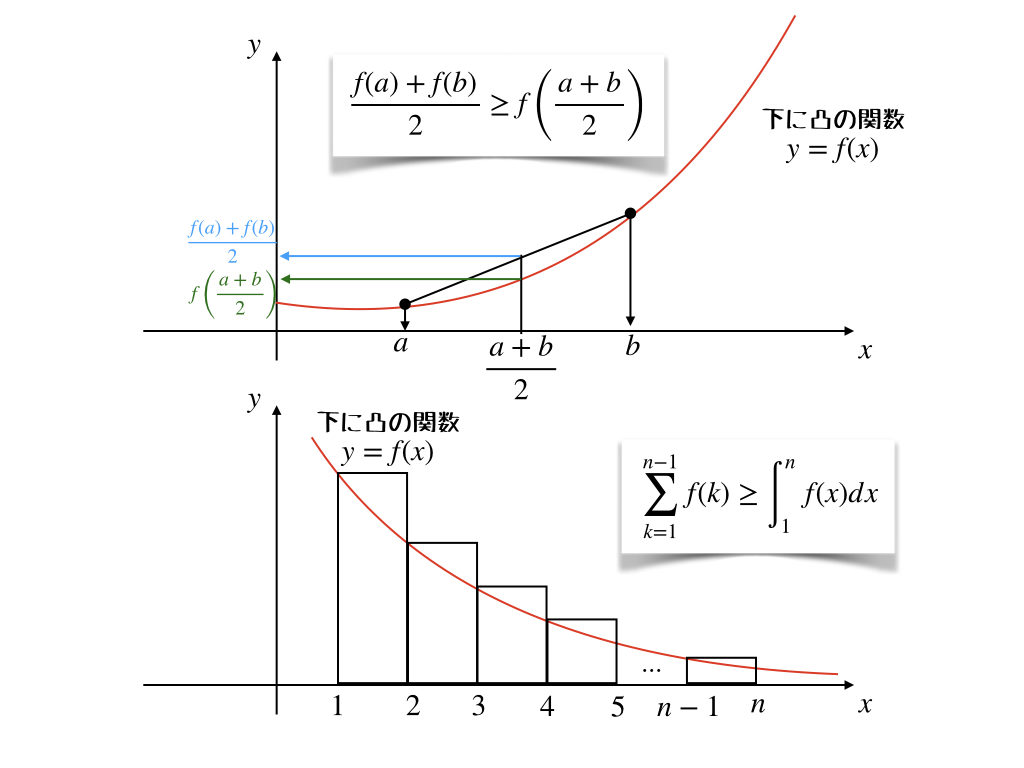
私が思いつくのはこの2つかな。
いいじゃん。あたしも同じものを想像してたよ。特に下の方、面積と積分の関係は最難関大学の入試ではたまに出てくるから、使えるようにしておくと便利だよね。
4つ目の近似の利用というのは、物理でもよく出てくるよ。でも不等式を証明するときにも使えるの?
う〜ん、物理の近似より、もっとしょぼいやつだよ。例えば、
\(\pi^{2}>9.8\)を示すようなときに、\(\pi=3.14\)として
$$\pi^{2} > 3.14^{2} > 9.8596$$
みたいに計算すること、かな。あんまり出てこないけど、数値計算の時とかにはよく使うよ。今日は、このテクニックを使う問題も用意しているよ。
へ〜。じゃあ、頭に入れておかないとね。数学的帰納法は最後に書かれているけど、実は結構重要だよね。
そうだったね。教科書にも、数学的帰納法で不等式を証明する例題があるくらいだからね。
じゃあ、そろそろ問題やる?
りょ〜かい。この問題からやってみようか。
2011年 第4問 ”\(\cdots\)”は帰納法のカモになる
$$(1-a_{1})(1-a_{2})\cdots(1-a_{n})>1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{n}}{2^{n-1}}\right)$$
が成立することを示せ。
こういう\(n\)個の文字の計算が出てきたら、帰納法でできたらいいなぁ、って考えちゃうけどね。
う〜ん、いいんじゃない。その発想で。帰納法でやってみようよ。
そうだねぇ。帰納法はまず初期条件が大事だから。
\(n=2\)のとき
(左辺)ー(右辺)\(=(1-a_{1})(1-a_{2})-1-(a_{1}+\frac{a_{2}}{2})\)
\(= a_{1}a_{2}-\frac{a_{2}}{2} = a_{2}\left(a_{1}-\frac{1}{2}\right)\)
で、\(a_{1}, a_{2}\)の条件から、これは正だね。
初期条件が正しいことがわかったら、いつもの通り、\(n=k\)の場合で正しいことを仮定して、\(k+1\)の場合でも正しいことを示せばいいね。
じゃあ、それ、やってみようか。
\(n=k\geq 2\)のとき不等式が成り立つとすると、\(\frac{1}{2}<a_{k+1}<1\)として
\((1-a_{1})(1-a_{2})\cdots(1-a_{k})(1-a_{k+1})\)
\(>\left(1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{k}}{2^{k-1}}\right)\right)(1-a_{k+1})\)
\(=1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{k}}{2^{k-1}}\right)-a_{k+1}\left(1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{k}}{2^{k-1}}\right)\right)\)
さて、ここまではいったけど。
そうだね。ここから、右辺が証明したい不等式の\(k+1\)バージョンになってくれればいいんだけどね。
う〜ん、ちょっとバカなことかもしれないけど、もう一度仮定を使って、二項目の\(\left(1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{k}}{2^{k-1}}\right)\right)\)を元に戻してみるのはどうだろう。二項目の符号はマイナスだから、不等号の向きは変わらなくて済むし。
お〜。それ、いい考えだよ。やってみて。
そう?
\((1-a_{1})(1-a_{2})\cdots(1-a_{n})(1-a_{k+1})\)
\(>1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{k}}{2^{k-1}}\right)-a_{k+1}(1-a_{1})(1-a_{2})\cdots(1-a_{k})\)
ていう感じ。あ、あれ、そうか。あとは\(a_{j}(j=1, 2, \cdots, k)\)に関する不等式を使って、\((1-a_{j})\)を全部\(\frac{1}{2}\)に変えちゃえばいいのか。
あたり! マイナスが付いているから、数を大きくする分には、不等号の向きは変わらないからね。今の場合、どんな\(j\)についても
$$1-a_{j} < \frac{1}{2}$$
が成り立つから。
そうすると、全部で\(k\)個かければいいんだから
\((1-a_{1})(1-a_{2})\cdots(1-a_{k})(1-a_{k+1})\)
\(>1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{n}}{2^{k-1}}\right)-\frac{a_{n+1}}{2^{k}}\)
\(=1-\left(a_{1}+\frac{a_{2}}{2}+\cdots+\frac{a_{k}}{2^{k-1}}+\frac{a_{k+1}}{2^{k}}\right)\)
となって、\(k+1\)の時も示すことができた。
これで、数学的帰納法によって、自然数\(n\geq 2\)について題意が成立することが証明できたね。
うん。幸先いいスタートになったね。次の問題はどうしよっかな。じゃあ、かなりオーソドックスな問題、典型的な不等式の証明問題をやろっか。
1991年 第4問 タンジェントに目が眩む
ようこちゃん、これを見て、最初に何を思う?
何をって、、、。タンジェントがいっぱいあるなぁ、ってことかな。
え? ま、まぁ、確かにね。でも、他にも色々気づくでしょ。
そうだねぇ。さっき確認したばかりっていうのもあるけど、右辺側は、なんか凸性が使える気がするけど。
そうだよね。この問題、左辺側も右辺側も両方とも引き算でやろうと思ったら、結構大変だよ。特に右辺はこの形がとても綺麗に「凸性」の性質を表しているんだから、その通りに計算してあげたいよね。
おっけい。じゃあ、先に右辺側から示そっか。
\(f(x) = \tan{x}\)とおくね。凸性があるかを調べよう。
$$f^{\prime}(x) = \frac{1}{\cos^{2}{x}}$$
$$f^{\prime\prime}(x) = \frac{2\cos{x}\sin{x}}{\cos^{4}{x}} = \frac{\sin{2x}}{\cos^{4}{x}} > 0\ \left(0\leq x < \frac{\pi}{4}\right) $$
だから、\(y=f(x)\)は、下に凸だね。つまり、
$$f\left(\frac{a+b}{2}\right) < \frac{1}{2}(f(a)+f(b))$$
となって、右辺側は証明できたね。
うん。凸性を知っていると、それを示すだけで、あっさり不等式が証明できることがあるから、とても重要だよ。じゃあ、左辺側はどうする?
う〜ん、どうだろ。相加・相乗平均が使えるような気もしたけど、無理かな。ひとまず、角度を\(\frac{a}{2}, \frac{b}{2}\)に統一してみよっかな。
おっ! 今度は、力押しだね。
なんか知ってる風な言い方だね。ま、でも計算するか。
$$\sqrt{\tan{a}\cdot\tan{b}} = \sqrt{\frac{2\tan{\frac{a}{2}}}{1-\tan^{2}{\frac{a}{2}}}\cdot\frac{2\tan{\frac{b}{2}}}{1-\tan^{2}{\frac{b}{2}}}}
= \frac{2\sqrt{\tan{\frac{a}{2}}\cdot \tan{\frac{b}{2}}}}{\sqrt{\left(1-\tan^{2}{\frac{a}{2}}\right)\left(1-\tan^{2}{\frac{b}{2}}\right)}}$$
$$\tan{\left(\frac{a+b}{2}\right)} = \frac{\tan{\frac{a}{2}}+\tan{\frac{b}{2}}}{1-\tan{\frac{a}{2}}\tan{\frac{b}{2}}}$$
で、え〜とどうしよう。
そうだねぇ。このやり方はちょっと大変かもね。
やっぱりね。先に言ってよ。
どうするかっていうと、やっぱり、左辺側も凸性を使いたいんだよ。
え? でも、全然そんな形してないし、そもそもどんな関数の凸性を見るの?
え? あたしには見えるけどな、その関数形。
私には見えないよ。
じゃあ、ヒント。左辺と右辺の両方に自然対数をとってみよう。どっちも正だから大丈夫だよね。
あ、ログ?
(左辺)\(= \log{(\tan{a}\cdot\tan{b}})^{\frac{1}{2}}\)
\(= \frac{1}{2}(\log{\tan{a}}+\log{\tan{b}})\)
あれ? なんか見えてきたかも。これで、中辺にもlogつけると
(中辺)\(= \log\tan{\left(\frac{a+b}{2}\right)}\)だから、結局
$$\frac{1}{2}(\log{\tan{a}}+\log{\tan{b}}) \leq \log\tan{\left(\frac{a+b}{2}\right)}$$
を示せばいいってことだね。
ね? 見えたでしょ。凸性を考える関数。
ここまでわかれば、ね。
$$g(x) = \log\tan{x}$$
の凸性を調べればいいんだね。じゃあ、計算してみるよ。
$$g^{\prime}(x) = \frac{1}{\tan{x}}\cdot\frac{1}{\cos^{2}{x}} = \frac{2}{\sin{2x}}$$
$$g^{\prime\prime}(x) = \frac{-4\cos{2x}}{\sin^{2}{2x}}$$
で今の\(x\)の範囲を考えると
$$g^{\prime\prime}(x) \leq 0$$
だから、今度は上に凸だね。上に凸の時は、不等号の向きが逆になるから、確かに
$$\frac{1}{2}(\log{\tan{a}}+\log{\tan{b}}) \leq \log\tan{\left(\frac{a+b}{2}\right)}$$
が成り立つんだ!
この問題はとても特殊だけど、凸性を示すだけで不等式の証明ができちゃうんだ。他にも凸性を考えると簡単に証明できる不等式がいっぱいあるから、大学受験では絶対に使えるようになっておいたほうがいいよ。
確かに。知らないと、絶対に思いつかない証明方法だもんね。
凸性関連だと、こんな問題なんかどう?
1999年 第3問 類は友を呼ぶ
$$\frac{{b_{1}}^{2}}{{a_{0}}^{2}+1}+\frac{{a_{1}}^{2}}{{b_{0}}^{2}+1} > \frac{{a_{1}}^{2}}{{a_{0}}^{2}+1}+\frac{{b_{1}}^{2}}{{b_{0}}^{2}+1}$$
(2) \(n\)個の自然数\(x_{1}, x_{2}, \cdots, x_{n}\)は互いに相異なり、\(1\leq x_{k}\leq n\ (1\leq k \leq n)\)を満たしているとする。このとき、次の不等式が成り立つことを示せ。
$$\sum_{k=1}^{n}\frac{{x_{k}}^{2}}{k^{2}+1} > n-\frac{8}{5}$$
凸性なんて、かけらも感じないけど、そういう問題なんだ。
ふふ。ようこちゃん、見た目に惑わされちゃ、ダメだよ。特に難関大学の入試ほど奥が深いんだから。
かもね。でも、どう見ても(1)は単に引き算すればうまくいきそうだから、そのまま計算してみるよ。
(左辺)ー(右辺) \( = \frac{{b_{1}}^{2}-{a_{1}}^{2}}{{a_{0}}^{2}+1} + \frac{{a_{1}}^{2}-{b_{1}}^{2}}{{b_{0}}^{2}+1}\)
$$ = \frac{ ({b_{1}}^{2}-{a_{1}}^{2})({b_{0}}^{2}+1) + ({a_{1}}^{2}-{b_{1}}^{2})({a_{0}}^{2}+1) }{ ({a_{0}}^{2}+1)({b_{0}}^{2}+1) }$$
$$ = \frac{ ({b_{0}}^{2} – {a_{0}}^{2})({b_{1}}^{2} – {a_{1}}^{2}) }{ ({a_{0}}^{2}+1)({b_{0}}^{2}+1) } > 0$$
だね。
うん。そうだね。じゃあ、次の(2)に行く前に、この式の意味をちょっと考えてみる? この式が主張していることは何だろう?
左辺の方が大きいってことでしょ。それか、右辺の方が小さい。
そうだけどさぁ。どういう場合に大きくなったり、小さくなるのかってこと。
そうだねぇ。小さいもの同士、大きいもの同士をくっつけた時に、より小さくなるのかな。
うん、それそれ。そのことを頭に入れて(2)に進むといいと思うんだ。
(2)での\((1\leq x_{k}\leq n\ (1\leq k \leq n))\)っていうのは、\(1\)から\(n\)までのどれか1つずつに対応している、ってことだよね。ちなみに、シグマの\(k\)も1から\(n\)まで動くってことだね。
問題は、\(x_{k}\)の並び順だね。どういう風に並んでいるのかってことだけど。ポイントは、左辺の式を下から抑えるような形で評価できればいいなぁ、ってことだよ。
あ、それで、(1)なのかな。小さいものは小さいもの同士で固めれば、より小さくなるっていう。つまり、\(x_{k} = k^{2}\)にしちゃえば、左辺より小さくなるんじゃないかな。
ナイス! ようこちゃん。でも、それ、ちゃんと証明できる?
証明かぁ。感覚的には当たり前なんだけど、数学だから証明しなきゃダメだよね。じゃあ、シグマの中の各項、\(\frac{x_{k}}{k^{2}+1}\)について考えよう。
下から\(k\)番目の項を順に見ていったとき、\(x_{i} = m > i\)となる\(1\leq i \leq n\)があったとする。このとき、\(x_{j}=i\)\((i < j,\ 1\leq j \leq n)\)となる\(j\)が必ず存在する。(1)の不等式より、
$$\frac{m^{2}}{i^{2}+1} + \frac{i^{2}}{j^{2}+1} > \frac{i^{2}}{i^{2}+1} + \frac{m^{2}}{j^{2}+1}$$
となるので、\(x_{i} = i\)と置き換えた方が、値は小さくなる。これをすべての\(k\)についてやれば、
$$\sum_{k=1}^{n}\frac{k^{2}}{k^{2}+1}$$
が最も小さくなることを示せる。
簡潔にまとまっていていいね。結局
$$\sum_{k=1}^{n}\frac{{x_{k}}^{2}}{k^{2}+1} > \sum_{k=1}^{n}\frac{k^{2}}{k^{2}+1}$$
まではわかったけど、さぁ、このあとどうする?
う〜ん。まぁ、とりあえずこんな感じ?
$$\sum_{k=1}^{n}\frac{{x_{k}}^{2}}{k^{2}+1} > \sum_{k=1}^{n}\frac{k^{2}}{k^{2}+1} = \sum_{k=1}^{n}\left( 1-\frac{1}{k^{2}+1} \right)$$
$$ = n – \sum_{k=1}^{n}\frac{1}{k^{2}+1}$$
でも、これって計算できないよね。
うん。大学の数学までやれば
$$\sum_{k=1}^{\infty}\frac{1}{k^{2}} = \frac{\pi^{2}}{6}$$
ってことは示せるけどね。
あっ、そっか。凸性を利用するって、ここで利用するんだね。特に\(n\)乗の分数和の評価をするときには、凸性が輝くもんね。
そうだよ。ようこちゃんが絵に描いてくれたじゃん。今回は下の方だよ。
そうだったね。\(f(x) = \frac{1}{x^{2}+1}\)とおくと
$$f^{\prime}(x) = \frac{-2x}{(x^{2}+1)^{2}}$$
$$f^{\prime\prime}(x) = \frac{(x^{2}+1)(6x^{2}-2)}{(x^{2}+1)^{4}} > 0 (x \geq 1)$$
だから、\(x\geq1\)では、下に凸の関数だね。そうすると、和を積分で評価できるようになるから
$$\sum_{k=1}^{n}\frac{1}{k^{2}+1} < \int_{0}^{n}\frac{1}{x^{2}+1}dx$$
だね。
そのままだと積分を計算するときに、ちょっと困るから、こんな感じで、評価する式を変えてみる?
$$\sum_{k=1}^{n}\frac{{x_{k}}^{2}}{k^{2}+1} > n – \sum_{k=0}^{n}\frac{1}{k^{2}+1} > n – \sum_{k=0}^{\infty}\frac{1}{k^{2}+1}$$
こうすると一番右の式は置換積分がしやすいと思うよ。
サンキュー。そっか。この形なら、置換したときに変換した変数の区間の値が求まるもんね。
$$\sum_{k=0}^{\infty}\frac{1}{k^{2}+1} < \int_{0}^{\frac{\pi}{2}}\frac{1}{\tan^{2}{\theta}+1}\cdot \frac{1}{\cos^{2}{\theta}}d\theta$$
$$ = \int_{0}^{\frac{\pi}{2}}d\theta = \frac{\pi}{2} < 1.6 = \frac{8}{5}$$
つまり、
$$\sum_{k=0}^{\infty}\frac{1}{k^{2}+1} < \frac{8}{5}$$
だから、
$$\sum_{k=1}^{n}\frac{{x_{k}}^{2}}{k^{2}+1} > n – \sum_{k=0}^{\infty}\frac{1}{k^{2}+1} > n – \frac{8}{5}$$
が証明できるね。
うん。こういう感じで、分数の何乗かの和を厳密に計算することは、高校数学ではできなくても、凸性を使って評価することはできるから、一つの武器として身につけておいた方がいいよね。
凸性はそろそろクリアだね。そろそろ、近似を使う問題もやってみたいな。
了解。じゃあ、これ。
1993年 第5問 偶奇の多数決
確率の問題が絡んでくるのね。
うん。京大は、確率を使って式を出させて、”極限試行”で極限の計算能力を試してきたり、こんな感じで不等式を評価させたりしてくるよ。でも、この問題は、確率を出すだけなら、簡単だと思うけど。
う〜ん。確かに、サイコロを使うくせに、偶数と奇数しか考えないんだったら、結局コインを使っているのと変わらないからね。どっちも1回のサイコロ投げで、\(\frac{1}{2}\)の確率なんだから、簡単か。例えば、偶数が\(n\)回出るってことは、奇数が\(n\)回出るってことだけど、確率は
$$_{2n}C_{n}\left(\frac{1}{2}\right)^{2n}$$
って感じで計算できるね。\(n\)回以上というなら、
$$P = _{2n}C_{n}\left(\frac{1}{2}\right)^{2n} + _{2n}C_{n+1}\left(\frac{1}{2}\right)^{2n}+\cdots+_{2n}C_{2n}\left(\frac{1}{2}\right)^{2n}$$
かな。
そうだね。ようこちゃんなら、この式をどうまとめていく?
どうするかなぁ。まぁ、とりあえずくくるよね。
$$P = \left(_{2n}C_{n} + _{2n}C_{n+1} + \cdots + _{2n}C_{2n}\right)\left(\frac{1}{2}\right)^{2n}$$
二項係数の和ときたら、あれかな?
うん、きっとそうだよ。
これ?
$$(1+1)^{2n} = _{2n}C_{0} + _{2n}C_{1} + \cdots + _{2n}C_{2n-1} + _{2n}C_{2n}$$
でも、これをそのまま使える? あ、待って。そのままじゃなくて、
$$_{2n}C_{k} = _{2n}C_{2n-k}$$
の関係を使えばいいのかな?
ちょうど\(_{2n}C_{n}\)以外は1組ずつペアができるよね。
うん。いい感じ!
なら
$$(1+1)^{2n} = 2^{2n} = _{2n}C_{n} + 2\left(_{2n}C_{n+1} + _{2n}C_{n+2} + \cdots + _{2n}C_{2n}\right)$$
とかけるから
$$2\left( _{2n}C_{n} + _{2n}C_{n+1} + _{2n}C_{n+2} + \cdots + _{2n}C_{2n} \right) = 2^{2n} + _{2n}C_{n}$$
となって、これを\(P\)に使って
$$P = \left( _{2n}C_{n} + _{2n}C_{n+1} + \cdots + _{2n}C_{2n-1} + _{2n}C_{2n} \right)\left(\frac{1}{2}\right)^{2n} = \frac{1}{2}+\frac{_{2n}C_{n}}{2^{2n+1}}$$
だよね。ここまでまとまったか。
さすが、ようこちゃん。あとは
$$\frac{_{2n}C_{n}}{2^{2n+1}} \geq \frac{1}{4n}$$
が示せるかどうかってところだ。
\(_{2n}C_{n}\)はバラしてみるのがいいかな。
$$\frac{_{2n}C_{n}}{2^{2n+1}} = \frac{(2n)!}{n! \cdot n!}\cdot \frac{1}{2^{2n+1}}$$
$$ = \frac{ 2n(2n-1)(2n-2)(2n-3)\cdots\cdots(3\cdot2\cdot1) }{ (n(n-1)(n-2)\cdots3\cdot2\cdot1)(n(n-1)(n-2)\cdots3\cdot2\cdot1)}\cdot \frac{1}{2^{2n+1}}$$
さて、どうしたらいいだろう。
いよいよ近似の利用の出番だ。目的の式をみると、分母と分子がほとんどキャンセルしていくと都合がいいよね。じゃあ、分子の値を少しずつ変えて、分母の値とキャンセルするためにはどうすればいいかな?
どうかなぁ? 例えば、分子の偶数部分とかは、2でくくれば
$$2n(2n-2)(2n-4)(2n-6)\cdots(6\cdot4\cdot2) = 2^{n}\cdot n(n-1)(n-2)\cdot3\cdot2\cdot1 = 2^{n}\cdot n!$$
みたいになって、分母と消える気がする。だから、奇数をいじればいいと思うんだけど。
うん。そうだよ。でも、奇数をどういじる?
例えば\((2n-1)(2n-3)(2n-5)\cdots5\cdot3\cdot1\)を\((2n)(2n-2)(2n-4)\cdots6\cdot4\cdot2\)みたいに変えてしまえば、同じように分母と消えてくれるけど。
発想はいいんだけど、それだと\(\frac{_{2n}C_{n}}{2^{2n+1}} \)より大きな値になっちゃうよ。数学で近似をするときは、証明したい式を見てより小さくしたいのか、大きくしたいのかを考えないと、途中でうまくいかなくなっちゃう。今は
$$\frac{_{2n}C_{n}}{2^{2n+1}} \geq \frac{1}{4n}$$
を示したいから、近似をした時に、左辺より小さい値を作らないとダメだよ。
そっかそっか。だったら
\((2n-1)(2n-3)(2n-5)\cdots 5\cdot3\cdot1\)を
\((2n-2)(2n-4)(2n-6)\cdots4\cdot2 = 2^{n-1}(n-1)!\)
に変えたらいいんだね。そうすると
$$\frac{_{2n}C_{n}}{2^{2n+1}} \geq \frac{ (2^{n}\cdot n!) \cdot (2^{n-1}\cdot (n-1)!)}{n!\cdot n!\cdot2^{2n+1}} = \frac{1}{4n}$$
となって、ぴったり!
うん! 気持ちいいよね! だから
$$P =\frac{1}{2} + \frac{_{2n}C_{n}}{2^{2n+1}} \geq \frac{1}{2} + \frac{1}{4n}$$
が証明できたね。
近似の利用って、違う値に置き換えて不等式で評価するためのものなんだね。
うん。物理では、不等式で評価するというより、三角関数とか対数関数を多項式で表して物理現象を考えることが多いよね。
そうだね。特に、高校物理では単振動の運動を考えるときによく使うよね。
まぁ、物理の話はおいといて。じゃあ、次はちょっと面白い不等式を紹介するね。
1978年 第1問 相加・相乗平均は知っているけど…
$$2\left( \frac{a+b}{2}-\sqrt{ab} \right) \leq 3\left( \frac{a+b+c}{3}-\sqrt[3]{abc} \right)$$
を証明せよ。また、等号が成立するのはどんな場合か。
なんかすごい不等式だね。それぞれ相加平均から相乗平均を引いた式になっているけど。
面白いよね、これ。さぁ、どうやって解く?
引き算でやってみたいけど、このまま右辺から左辺を引き算すると
$$c+2\sqrt{ab}-3\sqrt[3]{abc}$$
となるね。これを微分するのは面倒かな。
そうだね。累乗根が混じっているから面倒かも。でも、根号が消えてしまえばなんてことはない不等式だよね。
根号を消すときには、何乗かするのがいいけど、この式の場合は意味ないなぁ。
ようこちゃん、根号を消すもう一つの方法があるよ。
え? う〜ん。あ〜、置き換えか。
今の場合、2乗根と3乗根があるから、いっそ\(a = x^{6}, b = y^{6}, c = z^{6}\)と置き換えちゃうか。全部正の数だから、別に問題ないね。そうすると
$$f(x, y, z) = z^{6} -3x^{2}y^{2}z^{2} + 2x^{3}y^{3}$$
だから、これなら微分も楽だ。
他にもいくつか方法あるけど、これが大胆な方法かも。
\(x, y, z\)はどれも独立だから、例えば\(z\)で微分して
$$f^{\prime}(x, y, z) = 6z^{5} – 6x^{2}y^{2}z = 6z(z^{4}-(xy)^{2})$$
だね。これは、増減表をかくと明快だけど、\(z^{2} = xy\)のところで最小値になる。その時の値は\(f(x, y, z)\)に\(z^{2} = xy\)を入れて
$$f(x, y, z) = x^{3}y^{3}-3x^{3}y^{3}+2x^{3}y^{3} = 0$$
あ! 0になっちゃった。最小値が0ってことは、もう証明できたよね。
そうそう! もう一回微分しなきゃと思っていたら、ここで終わっちゃうんだよね。
ちなみに、等号成立条件も出てきて\(z^{2} = xy\)だから
$$c^{2} = ab$$
の時だね。
うん。形も綺麗だし、計算結果も綺麗でしょ。次は、問題そのものは難しくないんだけど、解析的に計算できない積分の式を不等式で評価するための重要な考え方を教えてくれる問題をやってみよう。
1975年 第2問 多項式に近似せよ
(2) $$\int_{0}^{k}\sqrt{x}\left( 1-\frac{x}{k} \right)^{k} < 1$$
を示せ (\(k\)は自然数)。
まみの、難しくない、はあまり信用できないけど、この問題は確かにやりやすいかも。(1)で示したことを(2)の\(x\)に適用して、計算できない積分式を評価するってことだね。
うん。積分関係の問題は、みたときに方針が決まりやすいものが多くって、実質正確な計算ができるかっていう勝負だからね。
(1)なんて、あれで一発じゃない?
そうだね。あれ、だね。
特別な不等式の活用ってやつだね。相加・相乗平均の公式で
$$\frac{1+x}{2} \geq \sqrt{x}$$
じゃん。引き算して微分、でもできるけど、時間節約。
いろんな武器を駆使して、時間は節約していかないとね。
(2)の式は、このままでは計算できないけど、計算する必要ないんだね。だから、不等式の形になっていて、(1)を使ってことなのか。
大学入試、というか高校生までは(1)みたいな誘導があって、それを使って(2)みたいな計算をすればいいんだよ。つまり、言われた通りに全部やっていればいいんだけど、大学生になったらこれを自分でやらないといけなくなる。計算できない積分の形を計算できる形に置き換えて、その値を評価するって感じでね。
つまり、(2)で出てくるような式に出くわして、例えば\(k\to\infty\)のときに、それが発散しないようなことを自分で証明しなければいけないときとかだね。(1)の式を自分で思いつかないとダメってことだ。
そういうこと。そういう意味で、この問題から積分値を評価するテクニックを知るのは重要なんだ。
なるほどね。じゃあ、今回は(1)の問題を “作ってくれたことに感謝しながら” (2)を解くことにするよ。
$$\int_{0}^{k}\sqrt{x}\left( 1-\frac{x}{k}\right)dx < \int_{0}^{k}\frac{1}{2}(1+x)\left( 1-\frac{x}{k} \right)dx$$
これは部分積分でいけそうだね。
$$\int_{0}^{k}\frac{1}{2}(1+x)\left( \frac{-k}{k+1}\left(1-\frac{x}{k}\right)^{k+1} \right)^{\prime}dx$$
$$ = \frac{1}{2}\left[ (1+x)\frac{-k}{k+1}\left( 1-\frac{x}{k} \right)^{k+1} \right]_{0}^{k} + \frac{1}{2}\frac{k}{k+1}\int_{0}^{k}\left( 1-\frac{x}{k} \right)^{k+1}dx$$
$$ = \frac{1}{2}\frac{k}{k+1}+\frac{1}{2}\frac{k}{k+1}\frac{-k}{k+2}\left[ \left( 1-\frac{x}{k} \right)^{k+2} \right]_{0}^{k}$$
$$ = \frac{1}{2}\left( \frac{k}{k+1} + \frac{k^{2}}{(k+1)(k+2)} \right)$$
$$ = \frac{k}{k+2} < 1$$
ってことで、計算は少し長かったけどなんとか証明できたかな。
うん。やっぱり、ようこちゃんは計算が得意だね。物理では、積分の計算がめっちゃ、大事だもんね。
そうだね。特に大学以降になると、微積分で物理が成り立っているくらいだからね。
不等式で積分が絡んだら、こんな感じで出題者が頭をひねって積分が計算できない式を「積分ができる式」に変えるような工夫をしてくれるんだよ。だから、こっちはその苦労を “忖度” して、ちゃんと計算してあげたいよね。
ていうか、合格するためには、ちゃんと計算しなくちゃ。
へへ。その通り。ところで、積分関連の問題で、なかなか斬新な問題があったよ。これは、もしかすると、かなり苦戦するかもしれない。
1981年 第6問 ガウシアンの登場
(1) \(0<a\leq x\)のとき
$$\int_{a}^{x}e^{-\frac{t^{2}}{2}}dt \leq \frac{1}{a}e^{-\frac{a^{2}}{2}} – \frac{1}{x}e^{-\frac{x^{2}}{2}}$$
(2) \(3<b\)のとき
$$\int_{3}^{b}e^{-\frac{t^{2}}{2}+2t}dt < e^{\frac{3}{2}}$$
おっ! ガウス関数。大学入試でも出てくるんだね。
さすが、ようこちゃん。ちなみに、ガウシアンの一般形、かける?
もちろん。
$$\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^{2}}{\sigma^{2}}}$$
だよね。\(\mu\)と\(\sigma\)は定数でね。定数としてごちゃごちゃくっついているのは、この関数の積分値
$$\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^{2}}{\sigma^{2}}} = 1$$
とするためだね。これを計算できるようになるのが、理系大学生の第一歩って感じがする。ちなみに、今回はそういった定数を全部無視して、つまり\(\mu=0, \sigma = 1\)としたものになっているよ。
うん。殻を全て脱ぎ捨てて、裸のガウシアンって感じ。どうやらこの問題では、ガウシアンの積分値が発散しないことを示そうとしているみたいだけど、ここで出てくる計算は正規分布の積分を扱う上でとても重要だから、理系大学生になるなら、覚えておいて損はないよ。(2)で現れる計算テクニック(というほどでもないけど)は重要かな。
うん。(2)の形を見ると、なんとなくどんなテクニックを使えばいいのか予想がつくけど、それより(1)の方が見た目より簡単じゃなさそう。
おっ! 気づいた? そうなんだよ、実は(1)はちょっと気づきにくいかも。
パッと見は、凸性が使えるような気もするんだけど、正規分布には一般的な凸性がないからなぁ。2回微分するとわかるけど、全ての範囲で成り立つ凸性はないよね。
うん、凸性は使えないと思うよ。
凸性が使えないとなると、積分を面積で評価するっていう手法も使えないなぁ。とはいえ、この積分は厳密に計算できないし。
う〜ん。そこが悩みどころだよね。じゃあ、どうするか。
なんか、うまい方法はないかなぁ。
ようこちゃん。こういう時は、原点回帰。単に引き算をするって方法でどうだろう?
え? 引き算?
$$F(x) = -\frac{1}{x}e^{-\frac{x^{2}}{2}}+\frac{1}{a}e^{-\frac{a^{2}}{2}}-\int_{a}^{x}e^{-\frac{t^{2}}{2}}dt$$
ってこと?
さて、ようこちゃん。これの最小値を求められるかな?
これの最小値? ってことは微分をするってことだけど、微分、、、微分できな、、、いや、あ、そうか。微分できるんだ。
$$\left(\int_{a}^{x}f(t)dt\right)^{\prime} = f(x)$$
だったね。
そう! ここで、これを使うのはあまり想像できないから、苦戦するかもしれないって言ったんだけど、そのまま計算するのはできないけど、実は微分はできるんだよ。そうすると増減表がかけるから、最小値が求まるかもしれない、ってことだね。
よし、じゃあ計算するよ。
$$F^{\prime}(x) = \frac{1}{x^{2}}e^{-\frac{x^{2}}{2}}+e^{-\frac{x^{2}}{2}}-e^{-\frac{x^{2}}{2}} = \frac{1}{x^{2}}e^{-\frac{x^{2}}{2}} > 0$$
あ、単調増加になった。ってことは、最小値は\(x = a\)だから
$$F(a) = 0$$
が最小値だ。あれ? ってことは、証明できたじゃん。
そうなんだよ。実は原点回帰の方法で求められるんだ。ちなみに、ちょっと頭を使うならこんな方法もあるよ。もし積分の式が
$$\int_{a}^{x}te^{-\frac{t^{2}}{2}}dt$$
だったら計算できるよね。この場合は
$$\int_{a}^{x}te^{-\frac{t^{2}}{2}}dt = e^{-\frac{a^{2}}{2}}- e^{-\frac{x^{2}}{2}}$$
ってなる。さて、ここで問題
\(\int_{a}^{x}ae^{-\frac{t^{2}}{2}}dt\)と\(\int_{a}^{x}te^{-\frac{t^{2}}{2}}dt\)はどっちが大きいかな?
え? \(t\)が\(a\)以上の範囲を動くから\(\int_{a}^{x}te^{-\frac{t^{2}}{2}}dt\)の方が大きいでしょ。
その通り。だから
$$\int_{a}^{x}ae^{-\frac{t^{2}}{2}}dt < \int_{a}^{x}te^{-\frac{t^{2}}{2}}dt = e^{-\frac{a^{2}}{2}}- e^{-\frac{x^{2}}{2}}$$
ってことになって
$$\int_{a}^{x}e^{-\frac{t^{2}}{2}}dt < \frac{1}{a}e^{-\frac{a^{2}}{2}}- \frac{1}{a}e^{-\frac{x^{2}}{2}}$$
だよね。今、\(a \leq x\)なんだから
$$\int_{a}^{x}e^{-\frac{t^{2}}{2}}dt < \frac{1}{a}e^{-\frac{a^{2}}{2}}- \frac{1}{a}e^{-\frac{x^{2}}{2}} \leq \frac{1}{a}e^{-\frac{a^{2}}{2}}- \frac{1}{x}e^{-\frac{x^{2}}{2}} $$
になるよね。
なるほど、ね。それは賢い方法かも。でも、思いつかないよ、普通。
まぁまぁ、引き算でできるなら、それでいいと思うんだけど、こういう風に積分を評価する方法もあるって知っとくのはいいかもよ。さて、この結果を使って(2)をときたいね。
そうだね。ただ、\(2t\)が邪魔だよ。
邪魔者は消してしまえ。
え?
なんてね。でも、数学では邪魔者を消すっていう発想は大事でね。
まぁ、言いたいことはだいたいわかるよ。この場合は、平方完成しろ、ってことだよね。
平方完成! その通り。ガウシアンの計算では、指数部分を平方完成することがよくあるから、頭に入れておくと大学になっても役に立つかも。
うん。それはそう思う。平方完成すると
$$\int_{3}^{b}e^{-\frac{t^{2}}{2}+2t}dt = \int_{3}^{b}e^{-\frac{1}{2}\left( (t-2)^{2} -4 \right)}dt$$
$$ = e^{2}\int_{3}^{b}e^{-\frac{(t-2)^{2}}{2}}dt$$
かな。これで(1)の結果を使うには、変数変換してやればいいね。\(s = t-2\)とすると
$$ = e^{2}\int_{1}^{b-2}e^{-\frac{s^{2}}{2}}ds$$
となるから、これなら(1)が使えて
$$ \leq e^{2}\left( e^{-\frac{1}{2}} – \frac{1}{b-2}e^{-\frac{(b-2)^{2}}{2}} \right) \leq e^{2}\cdot e^{-\frac{1}{2}} = e^{\frac{3}{2}}$$
となるわけか。スッキリ!
第6問らしく、最後はスッキリしているよね。どう? 不等式の証明って、楽しくない? いろんなバリエーションがあって、普段あまり使わないようなもの、例えば凸性とか近似とかが活躍するから、面白いと思うんだよね。
まぁね。今回のチョイスはそんなに計算が大変じゃないからかな。私は嫌いじゃないよ。
良〜し、じゃあ、もう1問おまけしちゃおう。ほんとはここで終わろうと思ったんだけど、サービス!
え? や、やっぱり、嫌いって言っとけばよかったか。
1973年 第5問 迷うな。やることはただ一つ。
$$f(x) = 1+\frac{x^{2}}{1\cdot2}+\frac{x^{3}}{2\cdot3}+\cdots\cdots+\frac{x^{n+1}}{n(n+1)}$$
とする。このとき、\(-1\leq x\leq 1\)において\(1\leq f(x) <2\)であることを証明せよ。
これはもう、あれっきゃないじゃん。
そんなことはないけど、まぁ、確かにすぐに思いつくのはそれかも。
微分だね。というか、私には微分しか見えないよ。いかにも微分してくれって形になっているからね。
$$f^{\prime}(x) = x+ \frac{x^{2}}{2} +\frac{x^{3}}{3} + \cdots\cdots+\frac{x^{n}}{n} = x\left(1+\frac{x}{2}+\frac{x^{3}}{3}+\cdots\cdots + \frac{x^{n-1}}{n}\right)$$
で、\(\left(1+\frac{x}{2}+\frac{x^{3}}{3}+\cdots\cdots + \frac{x^{n-1}}{n}\right)\)についてだけど、これは\(n\)がなんであろうと正になるね。もし\(n\)が偶数なら、2項ずつ順番にセットでまとめていけばどれも0以上(最初の1セットが常に正)になるし、もし\(n\)が奇数だとしても、最後の項が必ず0以上になって、それ以外を2項ずつまとめれば正になる。ってことは、\(x=0\)が唯一の\(f^{\prime} = 0\)の解だね。で、これが極小値になるんだ。
そうだね。ってことは、\(x=1\)か\(x=-1\)が最大値になるけど。
まぁ、明らかに\(f(-1) \leq f(1)\)だから、最大値は\(f(1)\)だね。
$$f(1) = 1+ \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\cdots\cdots+\frac{1}{n\cdot(n+1)} = 1+\sum_{k=1}^{n}\frac{1}{k(k+1)}$$
これは、いわゆる部分分数分解で計算できそう。
$$f(1) = 1+\sum_{k=1}^{n}\frac{1}{k(k+1)} = 1+\sum_{k=1}^{n}\left( \frac{1}{k}-\frac{1}{k+1} \right)$$
$$ = 2-\frac{1}{n+1} < 2$$
だね。
うん、完璧だね。不等式の問題はとりあえず、こんなところかな。
おっけい! ありがとう。
京大の問題は、難易度云々より、勉強になるテーマが多いから答えだけじゃなくて、問題を解く中で色々吸収していきたいことがあるんだよ。
そうだね。物理もそんな感じがするな。大問1つを解くと、その単元の総復習ができるって感じ。今度、物理の問題も紹介するね。
うん、よろしくね!



コメント