エレベーターとクレーンを具体例として巻上げ機の原理と所要出力の計算および変圧器の誘導起電力の計算について考える

問題リクエスト

巻上げ機に関する高校物理の力学の復習

物体を持ち上げる

質量\(m\) (kg)の物体に働く重力は、ニュートンによれば\(mg\)で与えられます。ここで\(g\)は重力加速度で、単位は\(\mathrm{m/s^{2}}\)です。この物体がある高さに静止していたとして、そこから上方に\(h\)だけ持ち上げたとすると、そのとき物体にした仕事は\(mgh\) (J)と計算されます。単位はジュールです。もし、エネルギーの原点を物体が最初に静止していた高さに設定すると、その物体は持ち上げられることにより、\(mgh\)のエネルギーを取得したことになります。この時のエネルギーを位置エネルギーとよびます。

さて、物体を持ち上げるための機械の出力を考えるためには、単位時間あたりにその物体にした仕事の大きさを求めることが必要です。単位時間あたりの仕事の大きさを求めるためには、その仕事にかかった時間\(t\)で割り算すればよいので、\(\frac{mgh}{t}\)と書けます。質量と重力加速度は時間によって不変であるとみなすことができるので、その物体が単位時間あたりに持ち上げられる距離\(\frac{h}{t} \mathrm{m/s}\)を求めればよいことがわかります。「単位時間あたりの距離」とはいわば速さと同じ概念であり、「単位時間あたりに持ち上げられる距離」というと、巻上機の場合では「巻上速度」と呼ぶことが多いです。そのため、巻上げに必要な出力は非常にシンプルに考えるならば、\(mgv\) (W)と考えることができます。機械電動機の問題では、これに様々な係数を乗除して実際のシステムの所要出力を計算します。

物体を摩擦抵抗に逆らって動かす

物体を水平方向に動かす場合、物体が接している面と物体に摩擦抵抗が存在しなければ、物体を動かすのに必要な力は0になり、結果として仕事は0です。ところが、摩擦抵抗が存在する場合は物体を動かすのに力が必要です。物体に働く摩擦力は摩擦係数\(\mu\)、質量\(m\)、重力加速度\(g\)を用いると\(\mu mg\) (N)と書くことができます。ここで機械工学では、\(\mu g\)を「横行抵抗」や「走行抵抗」などと呼び単位\(\mathrm{N/t}\)や\(\mathrm{N/kg}\)などを用いて一つの物理量として表すことが多いです。ここでは\(\mu g = \mu^{\prime}\)として抵抗係数と呼ぶことにします。この抵抗係数を用いると、摩擦に逆らって物体を\(h\)だけ動かすための仕事は、\(m\mu^{\prime}h\)と書けます。また、機械の所要出力については、単位時間あたりの仕事に直すので、\(m\mu^{\prime}v\)と書けます。ここでの\(v\)は横行速度や走行速度などと呼ばれます。

巻上機・横行機・走行機の所要出力

単位時間あたりに物体を持ち上げたり、摩擦に逆らって動かすための仕事を電動機の所要出力と結びつけます。電動機の所要出力を計算するためには、電動機の特徴的な値である「効率\(\eta\)」と安全ファクターである「余裕係数\(k\)」を考慮する必要があります。これらを用いると、はじめに巻上機の所要出力は重力加速度を9.8 \(\mathrm{m/s^{2}}\)として

$$P = \frac{9.8\times m_{1}\times v_{1} \times k}{\eta}$$

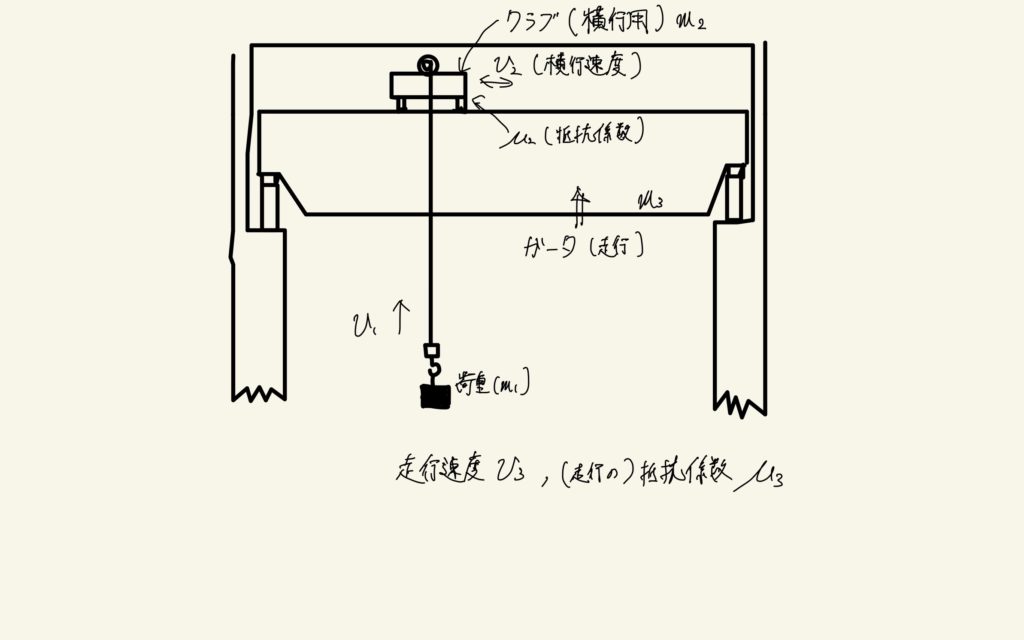
と計算できます。\(m_{1}\)は物体の質量、\(v_{1}\)は巻上速度です。またクレーンで物体を横行させる場合は

$$P = \frac{\mu_{1}(m_{1}+m_{2})v_{2}\times k}{\eta}$$

と計算できます。\(\mu_{1}\)は横行させる時の抵抗係数、\(m_{2}\)はクラブ質量、\(v_{2}\)は横行速度です。また走行する場合は

$$P = \frac{\mu_{2}(m_{1}+m_{2}+m_{3})v_{3}\times k}{\eta}$$

と計算できます。\(\mu_{2}\)は走行する時の抵抗係数、\(m_{3}\)はガータ質量、\(v_{3}\)は走行速度です。横行機と走行機に重力加速度がかかっていないのは、与えられている抵抗係数の中に、すでに重力加速度が考慮されているからです。実際の問題を解くときには、抵抗係数の単位がどのように与えられているかに注意することが必要です。もし、\(\mathrm{N/kg}\)と与えられているなら、質量はkgと直し、\(\mathrm{N/t}\)と与えられているなら、質量はtで表します。

エレベーター用電動機の所要出力

エレベーター用の電動機は基本的に巻上機と同じ要領で所要出力を考えることができます。少しトリッキーに見えるのは、対象となる質量です。エレベーターの概念図を示しました。ここで、エレベーターの箱部分（ケージ）の質量を\(m_{e}\)、物体の質量を\(m\)、エレベーターを持ち上げるための補完的な役割を果たしている平衡おもりの質量を\(m_{b}\)とします。このとき、平衡おもりの分だけ電動機の果たす役割を抑えることができるので、電動機にかかる質量は正味、\(m+m_{e}-m_{b}\)となります。この質量を先ほどの巻上機の所要出力の公式に当てはめればよいです。

$$P = \frac{9.8\times (m+m_{e}-m_{b})\times v \times k}{\eta}$$

で、\(v\)は昇降速度と呼ばれます。

変圧器における誘導起電力

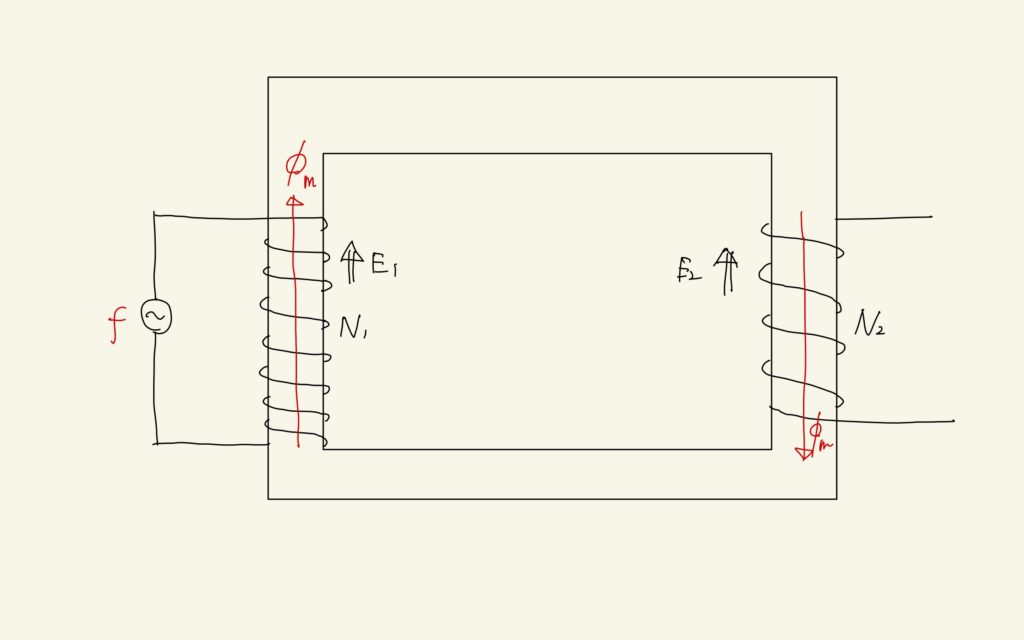
変圧器の基礎的な仕組みは、高校物理でも取り扱っています。ただ、高校物理では巻数の比が変圧器の電圧の比と等しいということくらいしか習いません。ここでは、変圧器にかかる誘導起電力まで見てみたいと思います。

\(N\)巻きコイルに働く誘導起電力\(E\)はコイル内の磁束の変化\(\frac{d\phi}{dt}\)を用いて

$$E = -N\frac{d\phi}{dt}$$

と書けます。ここで磁束の変化が三角関数である場合、特に、\(\phi = \phi_{m}\sin{\omega t}\)と選ぶならば、上の式を計算すると

$$E = -N\phi_{m}\omega \cos{\omega t}$$

と変形でき、ここで\(\omega\)は角振動数で、周波数\(f\)と\(\omega = 2\pi f\)という関係があるので、これを用いると

$$E = -2\pi fN\phi_{m}\cos{\omega t}$$

となります。ここで、マイナスを除いたこの式の係数\(2\pi fN\phi_{m}\)は得られる誘導起電力の最大値であり、通常「実効値」を用いて表記することが多いので、\(\sqrt{2}\)で割ったものが求める誘導起電力の実効値となります。

$$E_{eff} = \frac{2\pi}{\sqrt{2}}fN\phi_{m} \simeq 4.44\times fN\phi_{m}$$

これがN巻コイルで得られる誘導起電力（の実効値）です。なお、振動数の単位は[Hz], 磁束の単位は[Wb]です。実際の簡略計算では、4.44で表記されることが多いです。この式を用いるとある変圧器における\(N_{1}\)巻きコイルと\(N_{2}\)巻きコイルの誘導起電力の比は

$$E_{1} : E_{2} = N_{1} : N_{2}$$

となることが理解できます。

リクエスト問題の回答

問題１

巻上質量 50[t]，巻上速度 3.0[m/min]，横行速度 10.0[m/min]，走行速度 15.0[m/min]，クラブ重量 10.0[t]，ガータ質量 25.0[t]の天井クレーンがある。巻上用電動機，横行用電動機，走行用電動機の所要出力を求めよ。
ただし，機械効率は巻上装置 70%，横行装置 75%，走行装置 80%とし，横 行抵抗 100[N/t]，走行抵抗 150[N/t]とする。

先ほど提示したクレーンについての公式を参照すれば、それぞれの所要出力を計算することができますが、物理量の単位に注意しながら計算をすることが必要です。質量は巻上げの時にはkgに直します。また、時間の単位が”min”で与えられているので、これは”s”に直すことが必要です。

（１）巻上用電動機について

所要出力を求める公式はこちらです。

$$P = \frac{9.8\times m_{1}\times v_{1} \times k}{\eta}$$

ここでは余裕係数を考慮する必要がないので\(k=1\)とします。あとはそれぞれの物理量に値を代入します。答えはいずれも有効数字3けたで求めるとします。

$$P = \frac{9.8\times 50\times10^{3}\times \frac{3.0}{60} \times 1}{0.7} = 35000 [\mathrm{W}]$$

（２）横行用電動機について

所要出力を求める公式はこちらです。

$$P = \frac{\mu_{1}(m_{1}+m_{2})v_{2}\times k}{\eta}$$

同じように物理量に値を代入します。

$$P = \frac{100\times(50+10)\times \frac{10}{60} \times 1}{0.75} \simeq 1330 [\mathrm{W}]$$

（３）走行用電動機について

所要出力を求める公式はこちらです。

$$P = \frac{\mu_{2}(m_{1}+m_{2}+m_{3})v_{3}\times k}{\eta}$$

物理量に値を代入すると

$$P = \frac{150\times 85\times \frac{15}{60}\times 1}{0.8} \simeq 3980 [\mathrm{W}]$$

問題２

最大積載荷重が 1200[kg]，昇降速度が 120[m/min]のエレベータ用電動機 の所要出力を求めよ。ただし，平衡おもりの質量は，最大積載荷重の 50%に昇降箱の質量を加えたものとし，巻上装置の効率は 70%，加速に要する係数は 1.2 とする。

エレベータ用電動機の所要出力を求める公式は

$$P = \frac{9.8\times (m+m_{e}-m_{b})\times v \times k}{\eta}$$

ここで質量以外の物理量は単位を直してそのまま代入することができます。なお、加速に要する係数がここでは余裕係数とみなすことができます。質量は問題文の内容から計算する必要があります。求めたい質量は、最大積載荷重に昇降箱の質量を加え、そこから平衡おもりの分だけ引いたものです。最大積載荷重を\(m\), 昇降箱の質量をMとすると、平衡おもりの質量は0.5m + Mであり、求めたい質量は\(m+M-0.5m-M = 0.5m\)と得られます。ゆえに、エレベータ用電動機で対象となる質量は600 kgです。以上より

$$P = \frac{9.8\times 600\times \frac{120}{60}\times1.2}{0.7} = 20160 [W]$$

と計算できます。

問題３

一次巻数 900，二次巻数 30 の変圧器がある。磁束の最大値 0.03[Wb]， 周波数 50.0[Hz]として，巻数比と一次誘導起電力，二次誘導起電力を求めよ。

巻数比は、１次：２次 = 30 : 1より、通常\frac{N_{1}}{N_{2}}で求めるので、30と求められます。

（一次誘導起電力について）

誘導起電力を求める公式\(E_{eff} = 4.44\times fN\phi_{m}\)に値を代入すると

$$V_{1} = 4.44 \times 50 \times 900 \times 0.03 = 5994 \simeq 5990 [V]$$

$$V_{2} = 4.44 \times 50 \times 30 \times 0.03 = 199.8 \simeq 200 [V]$$

と計算できます。答えは有効数字3けたで求めています。

終わりに

計算ミスや議論の不備など発見された場合は、何卒ご指摘のほど、よろしくお願いいたします。