変圧器における電圧変動率の計算

問題リクエスト

変圧器における電圧変動率の定義

電圧変動率の定義自体は、電動機での定義と同じであり、負荷時の定格二次端子電圧\(V_{2,n}\)に対する無負荷時の定格二次端子電圧\(V_{2,0}\)の変化の割合と読むことができます。よって百分率の式で表すと

$$\epsilon = \frac{V_{2,0}-V_{2,n}}{V_{2,n}} \times 100$$

と表すことができます。

変圧器における電圧変動率の近似式

無負荷時の電圧を測定せず、定格負荷時の電圧と電流、およびそれぞれの抵抗やリアクタンスのみを用いて近似的に電圧変動率を計算することができます。まず、二次側に関わる主要な機器とその物理量を示した等価回路を考えます。

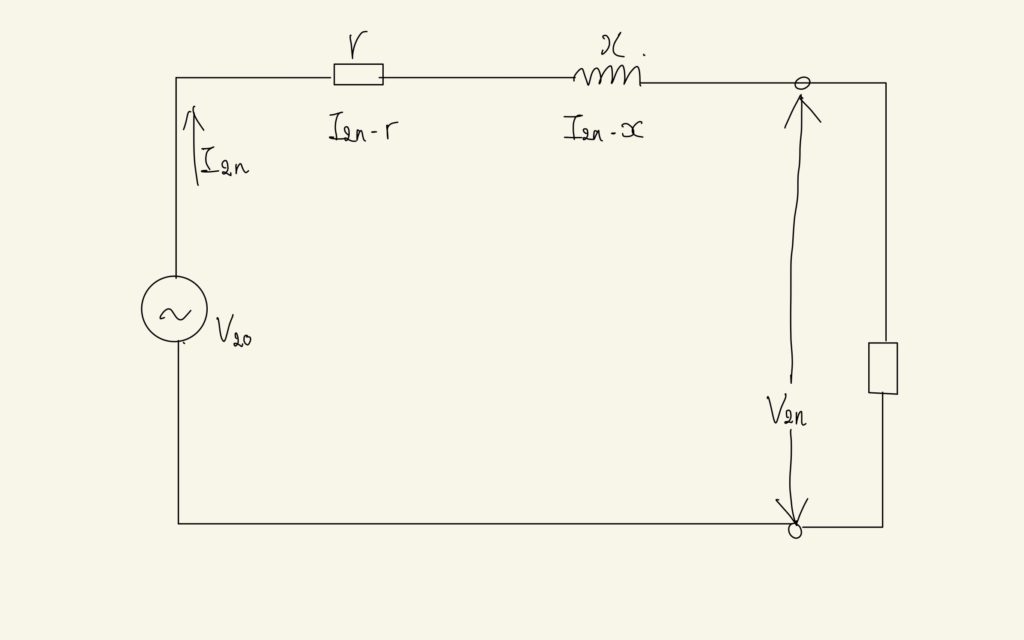
ここで、回路内の抵抗値の和を\(r\), 漏れリアクタンスの和を\(x\), 無負荷時電圧を\(V_{2,0}\), 負荷時の電圧、電流を\(V_{2,n}, I_{2, n}\)と表記します。この回路にはリアクタンスが含まれており、実際に流れている電流と電圧の位相がずれていることが考えられます。それを表す物理量が「遅れ力率」です。遅れ力率は、電流の位相が電圧に対して遅れていることを表す物理量です。端子電圧に対して、電流の位相が遅れ力率分だけ遅れていることを考慮して、電圧の関係性を図示すると以下のようになります。

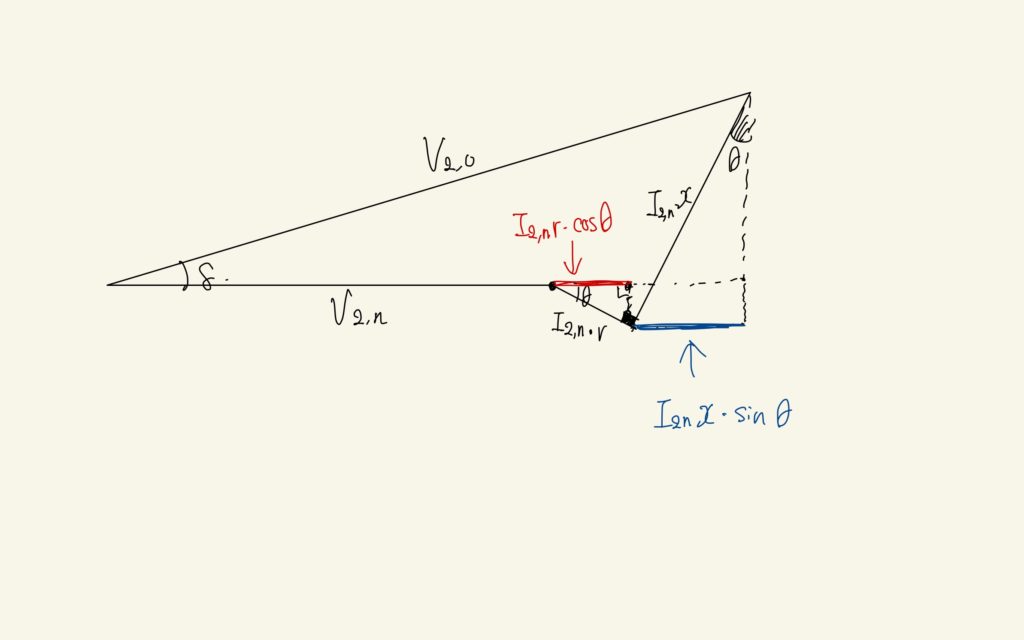
上の図では、遅れ力率に対応する位相のずれを\(\theta\)を用いて表しています。上の図について説明します。\(V_{2,0}\)については一旦無視しておきましょう。\(V_{2, n}\)に対して、電流の位相が\(\theta\)の分だけ遅れていることから、抵抗にかかる電圧も同様に同じだけずれていることになるので、上の図のような線分になります。\(V_{2,n}\)の線分から見ると折れ線になっているように見えます。次に、リアクタンスの部分については、コイルにかかる電圧は前回の記事で説明した通り、抵抗に流れる電流の位相に対して\(90度\)進んでいるように見えるので、\(I_{2,n}r\)に対して+90度分折れたような線分になります。リアクタンスにかかる電圧は\(I_{2,n}x\)とかけます。

ここからは高校数学の知識＋\(\alpha\)を用いて式を扱っていきます。まず、\(V_{2,0}\cos{\delta}\)に対応する部分を\(V_{2,n}\)などを使って表すと、
$$V_{2,0}\cos{\delta} = V_{2,n} + I_{2,n}r\cos{\theta}+I_{2,n}x\sin{\theta} = V_{2,n}+V^{\prime}$$
とかけます。ここで

$$V^{\prime} = I_{2,n}r\cos{\delta}+I_{2,n}x\sin{\theta} $$

と置いています。電圧変動率を求めるためには、\(V_{2,0}-V_{2,n}\)を求める必要があります。上で求めた式を用いると

$$V_{2, 0} – V_{2, n} = V_{2,0}-V_{2,0}\cos{\theta}+V^{\prime} = V_{2,0}(1-\cos{\delta})+V^{\prime}$$

と書くことができます。高校数学ではテーラー展開を習うことはありませんが、物理でもよく使う近似式として、\(x\)がほぼ0とみなせるときに成り立つとき
$$\sin{x} \simeq x, \cos{x} \simeq 1-\frac{1}{2}x^{2}$$
となることを学びます。上で、\(\delta\)がほぼ0とみなせると”仮定”すると

$$V_{2,0}-V_{2,n} = V_{2,0}\frac{1}{2}\delta^{2}+V^{\prime}$$

となり、今第1項が0とみなせることを利用すると

$$V_{2,0}-V_{2,n} \simeq V^{\prime} = I_{2,n}r\cos{\theta}+I_{2,n}x\sin{\theta}$$

となります。これを最初に述べた電圧変動率の定義式に代入すると

$$\epsilon \simeq \frac{I_{2,n}r\cos{\theta}+I_{2,n}x\sin{\theta}}{V_{2,n}}\times100$$

となりますが、これをさらに次のように変形します。

$$\epsilon \simeq \frac{I_{2,n}r}{V_{2,n}}\cos{\theta}\times100+\frac{I_{2,n}x}{V_{2,n}}\sin{\theta}\times100$$

このようにすると、百分率抵抗降下\(p\)と百分率リアクタンス降下\(q\)の定義

$$p=\frac{I_{2,n}r}{V_{2,n}}\times100, q = \frac{I_{2,n}x}{V_{2,n}}\times100$$

を用いて、電圧変動率を

$$\epsilon \simeq p\cos{\theta} + q\sin{\theta}$$

と見積もることができるようになります。注意点としては、この式はあくまで近似式であり、\(\delta \simeq 0\)とみなせるような状況でなければ十分な精度を持たないということを念頭に置いておく必要があります。通常、この近似式を用いるような問題では、「近似をしてもよい」という言葉に相当する文章が含まれています。そうでない場合には、できる限り定義式を用いて計算することになります。

変圧器における電圧変動率の近似式２

$$\epsilon \simeq p\cos{\theta} + q\sin{\theta}$$

この公式は、実はp, qに関する1次までの成分を取り出したもので、2次までの成分を取り出したものも有名です。そこで、その式も導出していこうと思います。すなわち、

$$V_{2, 0} – V_{2, n} = V_{2,0}-V_{2,0}\cos{\theta}+V^{\prime} = V_{2,0}(1-\cos{\delta})+V^{\prime}$$

ここで\(\delta^{2}\)の項を無視するのではなく、もう少し厳密に議論するということです。図のように\(V^{\prime\prime}\)を定義します。

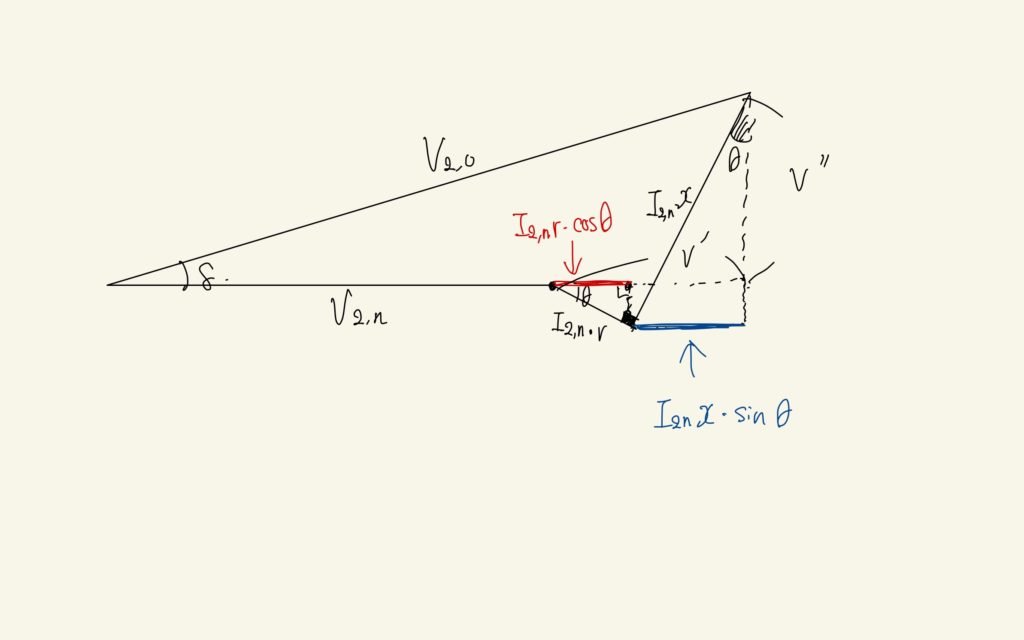
$$V^{\prime\prime} = I_{2,n}x\cos{\theta} – I_{2,n}r\sin{\theta}, V_{2,0} = \frac{V^{\prime\prime}}{\sin{\delta}}$$
が成り立ちます。

ここで三角関数の諸処の公式
$$1-\cos{x} = 2\sin^{2}{x}, \frac{1-\cos{x}}{\sin{x}} = \tan{\frac{x}{2}}$$
を用いると

$$\begin{eqnarray}
V_{2, 0} – V_{2, n} &=& V_{2,0}(1-\cos{\delta})+V^{\prime}\\
&=& V^{\prime\prime}\frac{1-\cos{\delta}}{\sin{\delta}} + V^{\prime}\\
&=& V^{\prime\prime}\frac{2\sin^{2}{\frac{\delta}{2}}}{2\sin{\frac{\delta}{2}}\cos{\frac{\delta}{2}}} + V^{\prime}\\
&=&V^{\prime\prime}\tan{\frac{\delta}{2}}+V^{\prime}\\
\end{eqnarray}$$
ここまでは近似を使っていません。ここから\(\delta\simeq0, \frac{V^{\prime}}{V_{2,n}} \ll 1\)を仮定すると
$$\begin{eqnarray}
V_{2, 0} – V_{2, n} &\simeq& V^{\prime\prime}\frac{1}{2}\tan{\delta}+ V^{\prime}\\
&=& V^{\prime\prime}\frac{V^{\prime\prime}}{V_{2, n} + V^{\prime}} + V^{\prime}\\
&=& \frac{V^{\prime\prime}}{V_{2, n}}\frac{V^{\prime\prime}}{1 + \frac{V^{\prime}}{V_{2,n}}} + V^{\prime}\\
&\simeq& \frac{(V^{\prime\prime})^{2}}{V_{2, n}}\ + V^{\prime}\\
\end{eqnarray}$$

のように近似ができ、電圧変動率の定義に代入して整理すると
$$\epsilon \simeq p\cos{\theta} + q\sin{\theta} + \frac{(q\cos{\theta} – p\sin{\theta})^{2}}{200}$$

となります。こちらも近似式ですが、より精度の高い計算ができます。

リクエスト問題の回答

リクエスト問題では、1の問題で電圧変動率の定義に沿った計算を行い、2の問題で電圧変動率の近似式を用いた計算を行うことが意図されているようです。2の問題において、近似を用いても良いという言葉がありませんが、題意を考えると明らかに近似式を使うことを要求しているので、ここでは近似式を用いて良いと考えられます。

問題１

定格二次電圧200[V]の変圧器の無負荷時の二次電圧を測定したところ、206[V]であった。この変圧器の電圧変動率を求めよ。

\(V_{2,0} = 206\)[V], \(V_{2,n} = 200\)[V]として、定義に代入して計算します。

$$\epsilon = \frac{206-200}{200}\times100 = 6$$
ご指摘をいただいたので以下のように修正します。ひどいミス。

$$\epsilon = \frac{206-200}{200}\times100 = 3$$

よって電圧変動率は6%3%です。

問題２

二次側から見た全抵抗0.30[Ω]、全漏れリアクタンス0.40[Ω]の変圧器に遅れ力率0.8の負荷を接続した時、二次電圧と二次電流は、定格二次電圧200[V]と定格二次電流10.0[A]になった。この変圧器の百分率抵抗降下と、百分率リアクタンス降下、電圧変動率を求めよ。

この問題では、すでに2次側から見た全抵抗、漏れリアクタンスを求めてくれているので、この値を使います。先の説明において、\(r = 0.3, x=0.4, I_{2,n} = 10.0, V_{2, 0} = 200, \cos{\theta} = 0.8\)とした場合に対応しているので、これらの値と公式を用いてそれぞれを求めます。

（１）百分率抵抗降下\(p\)

$$p = \frac{I_{2,n}r}{V_{2,n}}\times100$$

の公式に各値を代入すると

$$p = \frac{10\times0.3}{200}\times100 = 1.5$$

より百分率抵抗降下は1.5%です。

（２）百分率リアクタンス降下\(q\)

$$q = \frac{I_{2,n}x}{V_{2,n}}\times100$$

の公式に各値を代入すると

$$q = \frac{10\times0.4}{200}\times100 = 2$$

より百分率リアクタンス降下は2%です。

（３）電圧変動率\(\epsilon\)

無負荷時の電圧が与えられていないので、近似式で求めることになります。

$$\epsilon \simeq p\cos{\theta} + q\sin{\theta} $$

ただし、この近似式は\(\delta\simeq0\)とみなせるときに成り立ちます。このように近似できると仮定して計算を進めます。\(\sin^{2}{\theta} + \cos^{2}{\theta}=1\)という定理を用いると、\(\sin^{2}{\theta} = 0.36\)となり、正の方をとって\(\sin{\theta} = 0.6\)となります。

$$\epsilon \simeq 1.5\times0.8 + 2\times0.6 \simeq 2.4$$

ゆえに電圧変動率は2.4%と近似できます。

一応、より精度の高い近似式を用いて計算をしてみます。
$$\epsilon^{\prime} \simeq 2.4 + \frac{(2\times0.8 – 1.5\times0.6)^{2}}{200} = 2.40245$$
となり、有効数字2けたではやはり2.4%になります。

終わりに

電圧変動率を求めるときは、定義式で求められるときは定義式で、定義式では求められないような場合（無負荷時の電圧が記載されていない場合）には、近似式を使うことで求めることができます。

議論の不備、計算の間違いなどを発見されたときはご指摘いただけると幸いです。