眠る亀です。よろしくお願いします。最近、眠っている時間が安定しないので、どうしようもない時間に目が覚めて困ります。そういうときは、質問に答えていきましょう。
質問
高校数学の質問です。 画像のシュワルツの不等式のベクトルでの証明です。が、この波線がわかりません。初歩から解説よろしくお願いします。わかる方が全くおらず困ってます。

回答
画像をみる限り波線は4箇所あり、2次関数を用いた有名な証明方法とベクトルによる証明方法の2通りに関するものです。なるべく丁寧に答えていきたい思います。波線部に対応するところは大きなフォントにしようと思います。
(1)2次関数による証明
この証明方法は、考えた人が偉すぎるため、なぜその式が出てきたのかはわかりませんが、とにかくそういう風に関数を設定すれば証明できてしまう、という解法です。
$$f(x) = (ax-p)^{2} + (bx-q)^{2} + (cx-r)^{2}$$
と置きます。ここで出てくる文字は全て実数です。
左辺は実数の2乗の和の形をしているので、f(x)は0以上
であることがわかります。さらに、テキストにある通り、f(x)を展開すると
$$f(x) = (a^{2}+b^{2}+c^{2})x^{2}-2(ap+bq+cr)x+p^{2}+q^{2}+r^{2}$$
になり、a^{2}+b^{2}+c^{2}≠0と仮定すればf(x)は2次関数です。2次関数ならグラフがかけるので、f(x)≧0となるように書くと次のようになります。
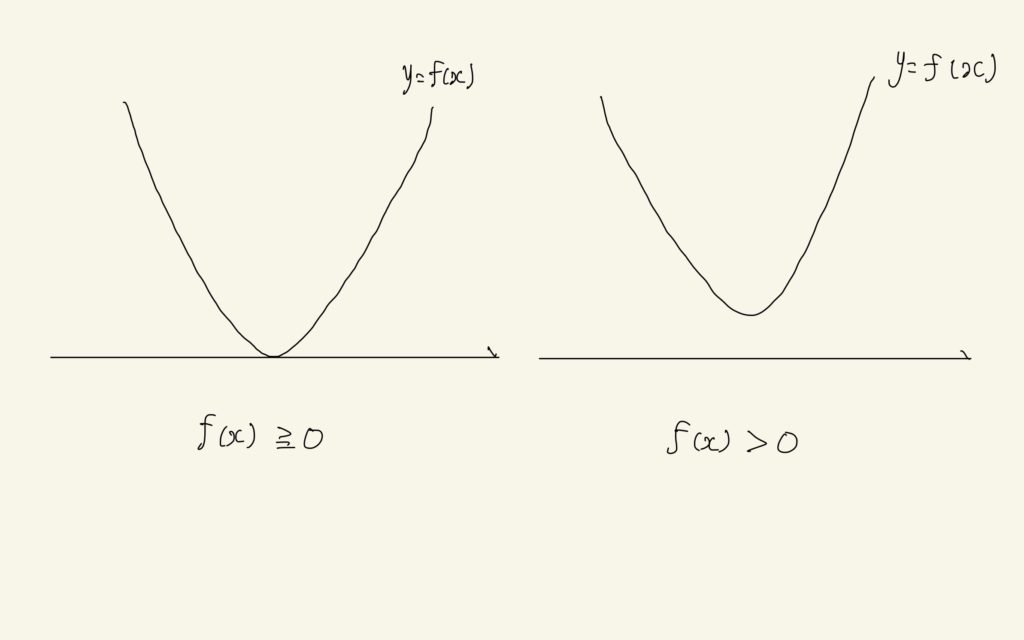
f(x)がxによらず常に0以上になるということは、x軸と共有点が一つか、または共有点がないという状況です。グラフで書くと上の図の左のパターンか右のパターンです。高校数学では、2次関数を2次方程式に関係づける解法がよく出てきます。この場合もf(x)=0という2次方程式を作ったときの解の個数が0か1つになるように判別式を設定すれば、上の状況を再現することができます。解の個数が0か1のときの判別式は0以下ですので、テキストにある通り
$$\frac{D}{4} = (ap+bq+cr)^{2}-(a^{2}+b^{2}+c^{2})(p^{2}+q^{2}+r^{2})\leq 0$$
となります。さて、判別式の等号が成り立つということはf(x)=0が成り立つxがただ一つ存在する、ということです。これは判別式の原理に戻れば良いです。判別式とは一般の2次方程式
$ax^{2}+bx+c=0$
の解
$$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$$
の根号の中身のことです。根号の中身が0なら解は1つしかありません。ゆえに、
判別式の等号が成り立つ(D=0となる)ことと、解が一つしかない(重解)ことは同値となります。
さらに、y=f(x)はxによらず常に0以上であることがわかっているので、f(x)=0が成り立つxが存在するためには、左のパターンにおいて、y=f(x)とx軸との共有点が1つだけになる状況しかありません。よって、f(x)=0となるようなxがそのまま重解となるので、f(x)の二乗の中身が全て0になるような条件が等号成立条件です。
(2)ベクトルを用いた証明
ベクトルの内積の関係を用いた証明です。こちらの方がまだ、直観に訴えてくるものがあるような気がします。内積の関係から
$$\overrightarrow{a}\cdot\overrightarrow{p}=\cos{\theta}|\overrightarrow{a}||\overrightarrow{p}|$$
ここで、θは二つのベクトルのなす角です。例えば次のような図をイメージできます。
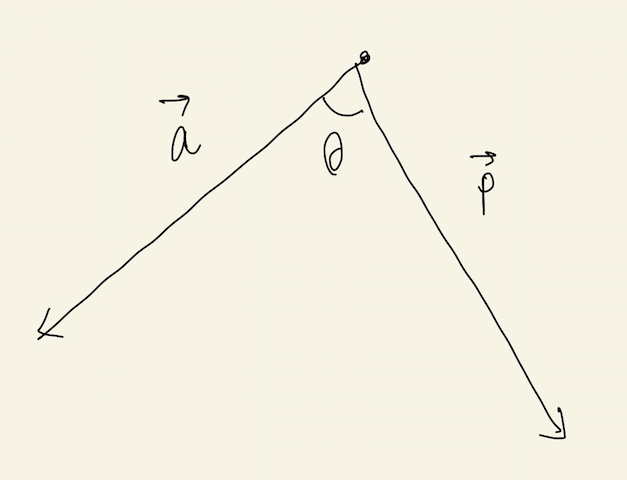
θによらず
$$|\cos{\theta}|\leq1$$
ですのでcosθがないほうが大きい値になります。
$$|\overrightarrow{a}\cdot\overrightarrow{p}| = |\cos{\theta}||\overrightarrow{a}||\overrightarrow{p}|\leq|\overrightarrow{a}||\overrightarrow{p}|$$
この式の両辺を二乗して
$$(\overrightarrow{a}\cdot\overrightarrow{p})^{2}\leq|\overrightarrow{a}|^{2}|\overrightarrow{p}|^{2}$$
さて、最後に等号成立条件ですが、この等号が成立するのは、大きな文字のフォントの式に戻って、cosθ=1とした場合です。すなわちθ=0°または180°の場合ですので、二つのベクトルが同じ方向か反対の方向、すなわち平行か反平行になるときです。よって、
$$\overrightarrow{a}//\overrightarrow{p}$$
のときが等号成立条件となります。

コメント