問題
中2です。問題を作ったので解いてくれると嬉しいです。
下の図のように、Oを中心とする小さい円と、O₁を中心とする大きい円が、大きい円の円周上にOが存在するように2点A,Bで交わっています。(以下図の上側から順にA,Bとします)
劣弧AB上に点Pを取り、半直線OPとOでない方の大きい円の円周との交点をQとします。線分PQの垂直二等分線と大きい円の円周との交点(2点あるうちの常に円の下半分にある方)をRとすると、A,P,Rは同一直線上にあることを示してください。
回答
いつもは口語調で書くのですが、今回は分量が多いので実際に「解答欄」に書くつもりで回答します。また三角法ですが、出題者を尊重して度数法で表します。
本回答で用いる記号を以下の図1に記す。本問の主張は条件を満たす任意のQについて成り立つ。ここで、∠QOT = θと定義する。また本問を通して点Oを中心とする円の半径をr, 点O1を中心とする円の半径をRとする。

補題1
本問の主張は、以下と同値である。
$$\stackrel{\frown}{BR} = \stackrel{\frown}{RQ} or BR = RQ$$
補題1の証明
以下の図2を用いて説明する。
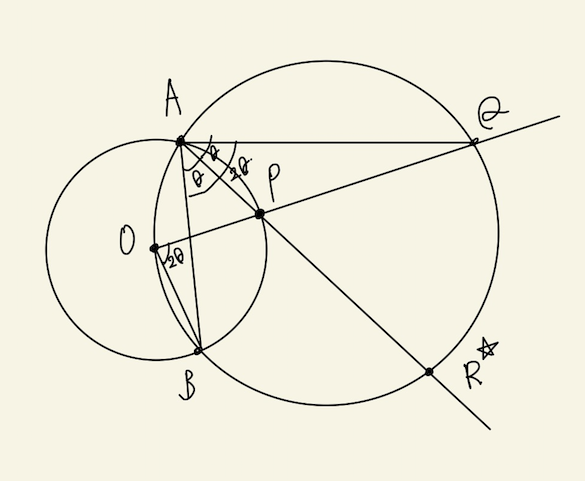
点A, Pを結ぶ直線と円O1との交点をR*とおく。円Oに円周角と中心角の関係、円O1に円周角の定理を用いることにより、
$$\angle{BAR^{*}} = \angle{QAR^{*}} \leftrightarrow \stackrel{\frown}{BR^{*}} = \stackrel{\frown}{R^{*}Q}$$
点Oを含まない弧BQを二等分する円O1上の点は一つしか存在しないため
$$\stackrel{\frown}{BR} = \stackrel{\frown}{RQ}$$
が成り立つとき、直ちにR*とRは等しくなる。ゆえに、3点A, P, Rが同一直線上に存在することが示される。よって補題1が示された。
補題2
θ=0°のとき、本問の主張が成り立つ
補題2の証明
θ=0°のとき、各記号の位置関係を図に記すと以下の図3で表される。
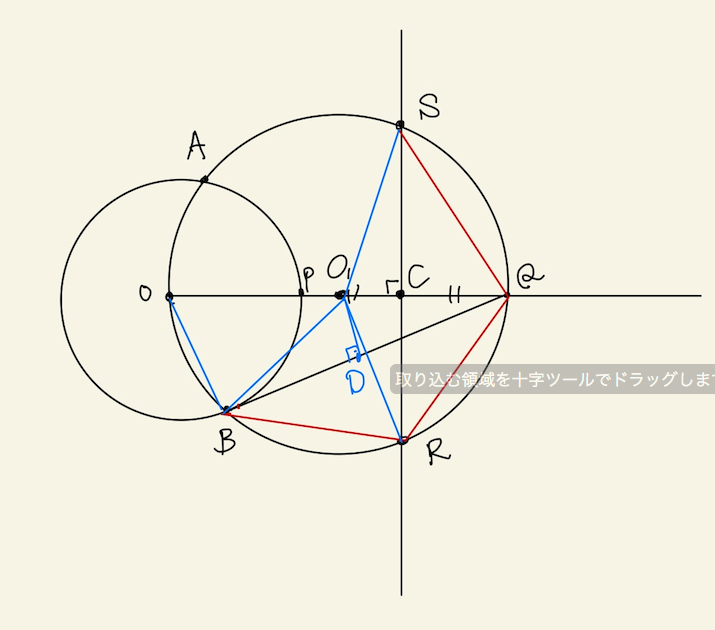
新たな記号C, Dはそれぞれ点O1からの線分SR, BQへの垂線の足を表す。以下、BQ=SRを示す。なぜなら、これが成り立つことで△BRQ≡△RQSを容易に示すことができ、合同な三角形の性質からBR=RQを示すことができる。補題1より、これは補題2を示すことに他ならない。
条件から成り立つPC = CQ、および円の半径の性質を考慮することで
$$O_{1}C = \frac{r}{2}$$
を求めることができる。また、△OBQと△O1DQの相似の性質から
$$O_{1}D = \frac{r}{2}$$
である。以上の事実と三平方の定理を用いて
$$BQ = RS$$
円周角の定理や上の結果を用いると
$$\angle{QBR} = \angle{SRQ},\ \angle{BQR} = \angle{RSQ}$$
を示すことができるので、△BRQ≡△RQSである。ゆえに対応する辺が等しいことからBR=RQ。
よって補題2は示された。
本問の証明
条件を満たす一般の角度θに対して、本問の主張が成り立つことを示す。以下の図4に改めて定義する記号を書き加える。
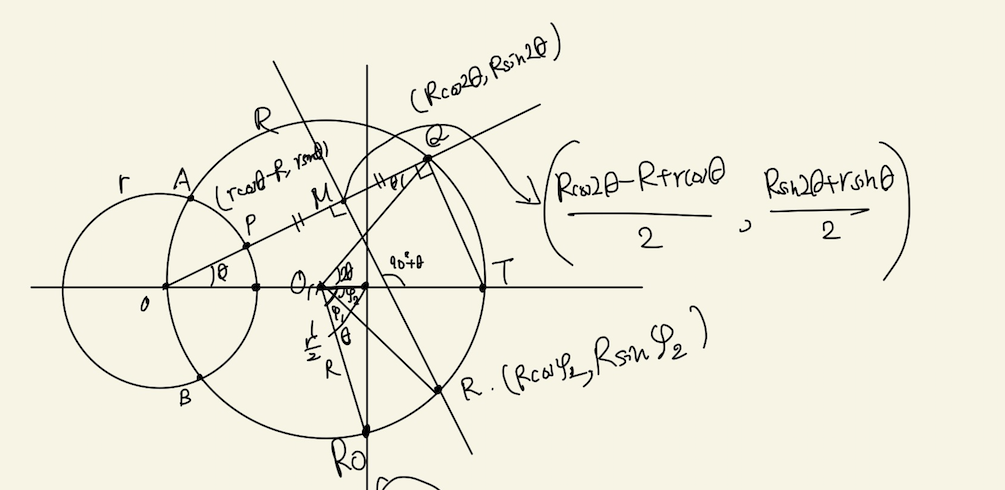
線分PQの中点をM, 補題1の場合におけるRをR0, また以下の角度を定義する。
$$\angle{TO_{1}R_{0}}= \psi_{1}, \angle{TO_{1}R} = \psi_{2}$$
このように定義すると、点O1を(0, 0)として点P, Q, R, Mの座標が図4のように定まる。すなわち
$$P(r\cos{\theta}-R, r\sin{\theta}), Q\left(R\cos{2\theta}, R\sin{2\theta}\right), R(R\cos{\psi_{2}, R\sin{\psi_{2}}})$$
$$M\left(\frac{R\cos{2\theta}-R+r\cos{\theta}}{2}, \frac{R\sin{2\theta}+r\sin{\theta}}{2}\right)$$
また、Ψ1に関しては補題1で得られたことから
$$\cos{\psi_{1}} = \frac{r}{2R}$$
ここで、直線MRは直線PQと垂直に交わることから以下が成り立つ。
$$\frac{R\sin{\psi_{2}}-\frac{R\sin{2\theta}+r\sin{\theta}}{2}}{R\cos{\psi_{2}}-\frac{R\cos{2\theta-R+r\cos{\theta}}}{2}} = -1\frac{\cos{2\theta}+1}{\sin{2\theta}}$$
適切に加法定理を用いると、以下の式となる。
$$R\cos{(\psi_{2}-2\theta)}+R\cos{\psi_{2}-r\cos{\theta}} = 0$$
$$\psi_{2} = \psi_{k}+\theta$$
とおくとこの式はさらに
$$2R\cos{\psi_{k}}\cos{\theta} – r\cos{\theta} = 0 \leftrightarrow \cos{\psi_{k}} = \frac{r}{2R}$$
となる。この変形ではθが条件を満たしながら動くとき、RはR0からTまでしか動かないのでθが90°とならないことを用いている。また、これを満たすΨkは一意に定まり、
$$\psi_{k} = \psi_{1}$$
よって
$$\psi_{2} = \psi_{1} + \theta \leftrightarrow \psi_{2}-\psi_{1} = \theta$$
補題2より、θ=0°のとき弧BR = 弧RQであった。θが動くと弧RQは2θに対応する分だけ動く。同時に弧BRはθに対応する分だけ動く。すると正味の値で、弧RQと弧BRが変化した長さは等しい。ゆえに条件を満たす任意のθにおいて
$$\stackrel{\frown}{BR} = \stackrel{\frown}{RQ} $$
補題1より、本問の主張が成り立つ。
前半も後半も素晴らしい補助線が引ければ、エレガントに解けるのでしょうね。補助線は苦手なので、計算に頼ってしまいます。そういえば、ラングレーの問題も三角法で解いた気がします。
上の回答が正しい議論かどうかはわかりませんが、とても面白かったです。

コメント