眠る亀と申します。今回は、任意の三角形の1点から下ろした垂線の足による1辺の内分比に関する質問がありました。興味深い題材でしたので、この質問にお答えしようと思います。今回は、ブログ内でLATEXを使うためのプラグインを導入しましたので、それも試したいと思います。
質問
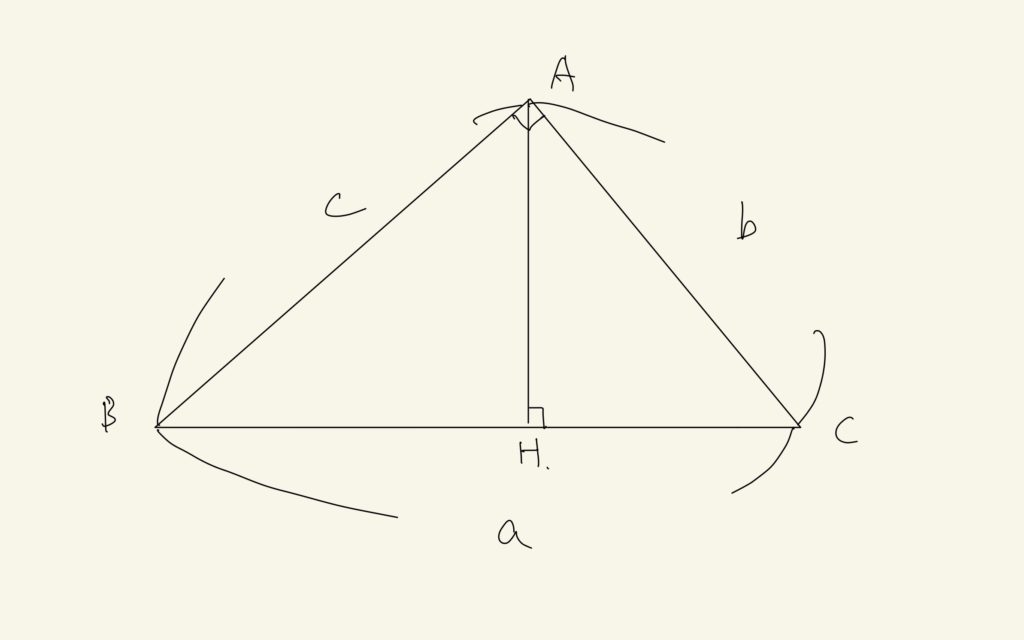
任意の△ABCにおいて、三辺AB BC CAの長さをそれぞれc a bとする。
いま点Aから対辺BCに下ろした垂線の足をHとするとき、Hが辺BCの如何なる内分点になるか答えなさい。すなわち、BH:HCをa b cで記述しなさい。
さらに は同様な考察を直角三角形と鈍角三角形でも行いなさい。
という問題があります。
鋭角三角形の場合は
√(c²−h²):√(b²−h²)
が最善の答えなのでしょうか…?
また、直角三角形の場合はBHもしくはHCのどちらかが0、鈍角三角形の場合は垂線の足が三角形の外側にできる、で合ってるのでしょうか?
回答
高校数学での解法
任意の三角形で、かつどの角が直角・鈍角かで求め方が変わるので、かなり計算のパターンがあります。一つ一つ丁寧に解いていこうと思います。
(1)鋭角三角形の場合
鋭角三角形の場合は、どの角も鋭角のため、ここでは場合わけをする必要がありません。記号を次のように定義します。
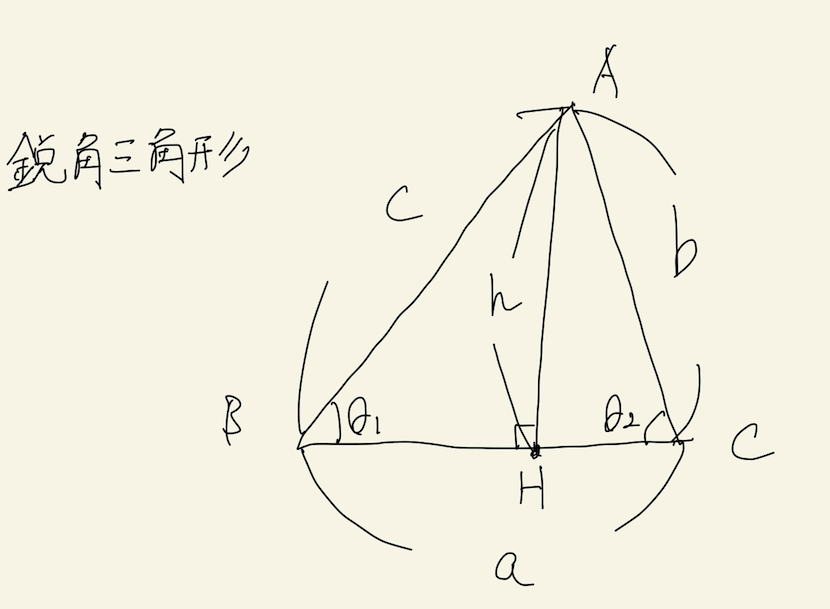
$$\mathrm{BH}:\mathrm{CH} = c\cos{\theta_{1}} : b\cos{\theta_{2}}$$
cosθは余弦定理よりa, b, cを用いて次のように求めることができる。
$$\cos{\theta_{1}} = \frac{a^{2}+c^{2}-b^{2}}{2ac}$$
$$\cos{\theta_{2}} = \frac{a^{2}+b^{2}-c^{2}}{2ab}$$
よって、BH:CHはa, b, cを用いて次のように表せる。
$$\mathrm{BH}:\mathrm{CH} = a^{2}+c^{2}-b^{2} : a^{2}+b^{2}-c^{2}$$
(2)直角三角形の場合
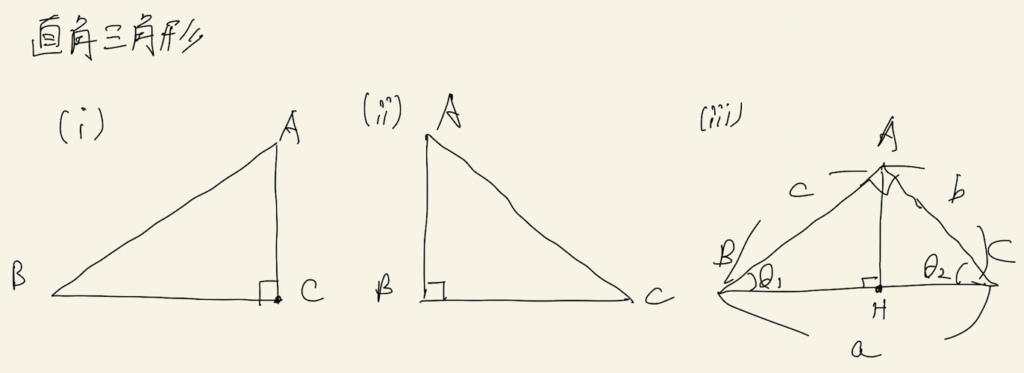
直角三角形と言っても、3通りの可能性があります。それぞれで計算方法が異なるので、以下のように場合分けします。
(2−1)直角三角形の場合 (C=90°)
CH=0なので、BH:CH = a : 0となります。
(2−2)直角三角形の場合 (B=90°)
BH=0なので、BH:CH = 0 : aとなります。
(2−3)直角三角形の場合 (A=90°)
$$\mathrm{BH}:\mathrm{CH} = c\cos{\theta_{1}} : b\cos{\theta_{2}}$$
$$\cos{\theta_{1}} = \frac{c}{a}$$
$$\cos{\theta_{2}} = \frac{b}{a}$$
BH:CHはa, b, cを用いて次のように表せる。
$$\mathrm{BH}:\mathrm{CH} = c^{2} : b^{2}$$
(3)鈍角三角形の場合
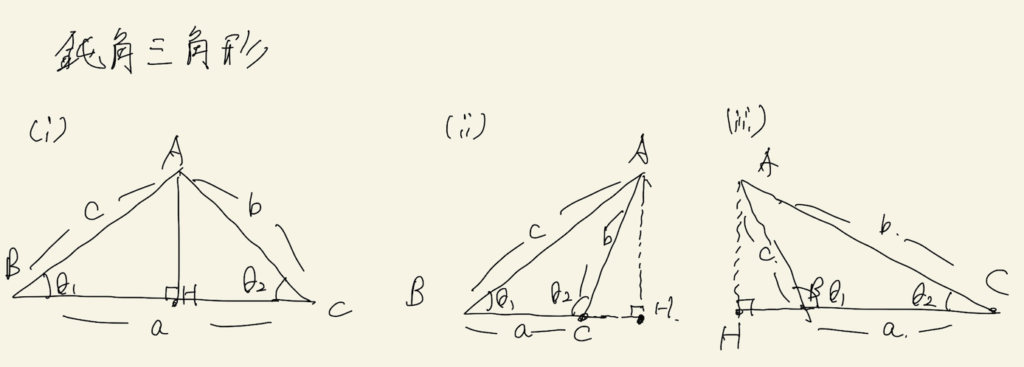
直角三角形のときと同様に、3通りの場合わけが必要です。
(3−1)鈍角三角形の場合 (A>90°)
この場合は、(1)の鋭角三角形と同様の計算が可能で、比の値も同じです。
$$\mathrm{BH}:\mathrm{CH} = a^{2}+c^{2}-b^{2} : a^{2}+b^{2}-c^{2}$$
(3−2)鈍角三角形の場合 (C>90°)
C>90°のときは、質問者様の言う通り、垂線の足が三角形の外にできるため、次のように計算されます。
$$\mathrm{BH}:\mathrm{CH} = c\cos{\theta_{1}} : -b\cos{\theta_{2}}$$
$$\cos{\theta_{1}} = \frac{a^{2}+c^{2}-b^{2}}{2ac}$$
$$\cos{\theta_{2}} = \frac{a^{2}+b^{2}-c^{2}}{2ab}$$
$$\mathrm{BH}:\mathrm{CH} = a^{2}+c^{2}-b^{2} : -(a^{2}+b^{2}-c^{2})$$
(3−3)鈍角三角形の場合 (B>90°)
この場合は、3-2と符号の関係が逆になります。
$$\mathrm{BH}:\mathrm{CH} = -(a^{2}+c^{2}-b^{2}) : a^{2}+b^{2}-c^{2}$$
こんな感じでしょうか。
中学数学での解法
(1)鋭角三角形の場合
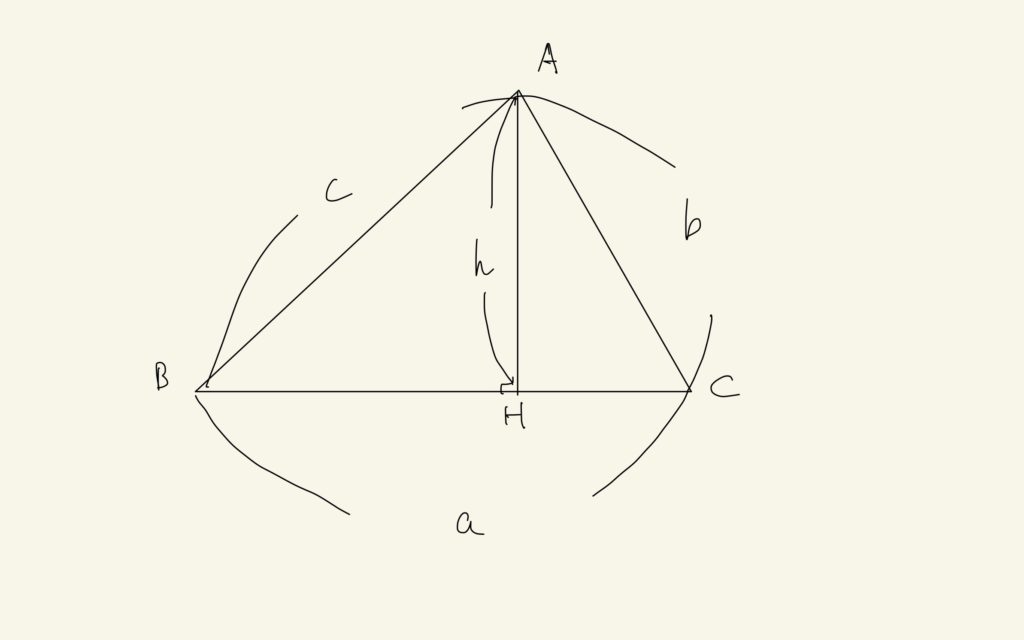
点Aから辺BCに下ろした垂線の長さをhとします。△ABHに三平方の定理を用いて
$$h^{2}+BH^{2} = c^{2}$$
△AHCに三平方の定理を用いて
$$h^{2}+(a-BH)^{2} = b^{2}$$
この二つの式について、辺々引いてhを消去すると、
$$BH^{2}-(a-BH)^{2} = c^{2}-b^{2} \leftrightarrow -a^{2} +2aBH = c^{2}-b^{2}$$
よって、BHを求めることができます。
$$BH = \frac{a^{2}+c^{2}-b^{2}}{2a}$$
CHも同様に求めることができます。
$$CH=a-BH = a- \frac{a^{2}+c^{2}-b^{2}}{2a}$$
$$CH=a-BH = \frac{a^{2}+b^{2}-c^{2}}{2a}$$
以上から、BH:CHの比は前の回答と同じく
$$\mathrm{BH}:\mathrm{CH} = a^{2}+c^{2}-b^{2} : a^{2}+b^{2}-c^{2}$$
となります。
(2)直角三角形の場合
BH=0やCH=0となる場合は、前の回答と同じで良いと思うので、A=90°のときのみを考えます。
実は最後の答えまでは上と同じ計算でたどり着きます。
$$\mathrm{BH}:\mathrm{CH} = a^{2}+c^{2}-b^{2} : a^{2}+b^{2}-c^{2}$$
ここから、直角三角形における性質
$$b^{2}+c^{2} = a^{2}$$
を上式に代入します。BHに関しては、a^2-b^2 = c^2, CHに関してはa^2-c^2 = b^2とします。
$$\mathrm{BH}:\mathrm{CH} = 2c^{2} : 2b^{2} = c^{2} : b^{2}$$
です。
(3)鈍角三角形については、Aが鈍角である場合は(1)と同様です。BかCが鈍角である場合を考えます。ここでは、考え方が重複してしまうのでBが鈍角である場合のみを考えます。
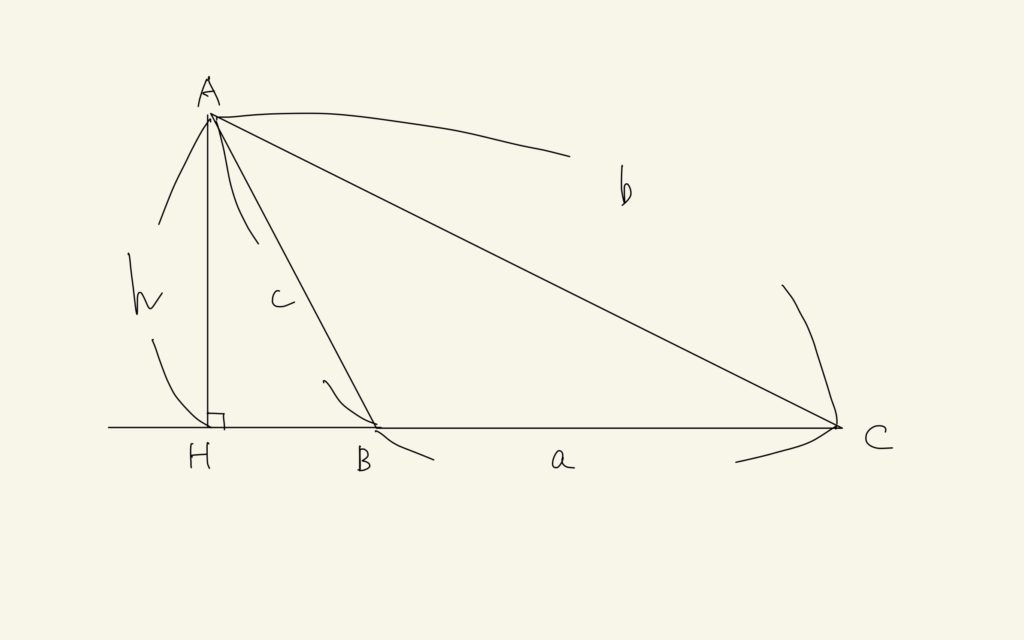
△ABHに三平方の定理を用いると
$$BH^{2}+h^{2} = c^{2}$$
△ACHに三平方の定理を用いると
$$(a+BH)^{2}+h^{2}=b^{2}$$
これらを先ほどと同様にhを消してBH, CHを求めると
$$-a^{2}-2aBH = c^{2}-b^{2} \leftrightarrow BH = -\frac{a^{2}+c^{2}-b^{2}}{2a}$$
$$CH = a+BH = \frac{a^{2}+b^{2}-c^{2}}{2a}$$
となるので、結局BH:CHは以下のように、前の回答と同じものを得ます。
$$\mathrm{BH}:\mathrm{CH} = -(a^{2}+c^{2}-b^{2}) : a^{2}+b^{2}-c^{2}$$

コメント