………。
あ。ようこちゃん。数学やってるね。平面図形の問題か。
まみ。この問題知ってる?
もちろん。中学生でも解けるって評判の問題だよね。
う〜ん。ただ、どうしてもベクトルでしか解けないんだよ。ベクトルに慣れすぎて、他の解法を考える気力が起きないんだよね。
ようこちゃん。確かにベクトルはとても便利な方法だけど、状況によってはベクトルで解くと計算量が大幅に増えちゃって、計算する気力がなくなるような問題だってあるんだよ。そういう時は、初等幾何とか場合によっては座標平面上に図形を置いてしまった方がいい場合もあるんだ。
ちなみに。この問題の場合は? 他の方法でも解けるの?
もちろん! 初等幾何でも解けるし、なんなら、座標平面に置いても解けるよ。
へ〜、そうなの?
よし、じゃあ、今日はようこちゃんのために、平面図形の解法をおさらいしよう! 最初に、ようこちゃんの解いている問題を使って、3つの方法を紹介するよ。
あ、ありがとう。よろしくお願いします。
2013年 第1問 導入にはうってつけ
じゃ、最初は初等幾何からやろうか。
初等幾何による解法
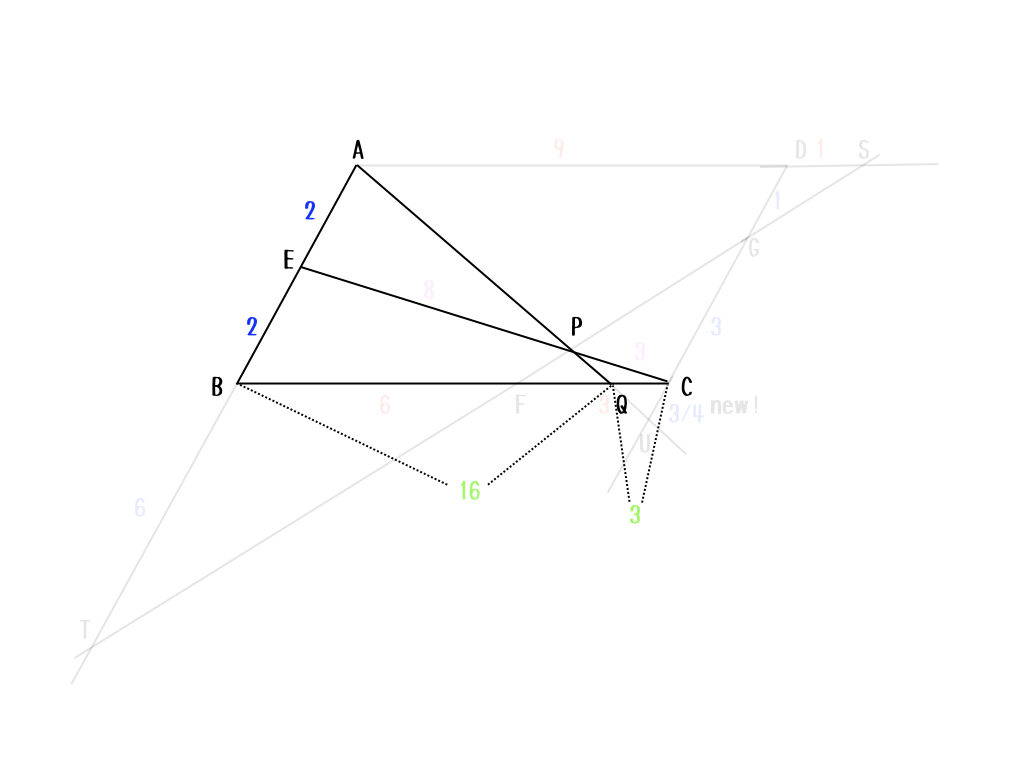
初等幾何で解くための生命線は「辺の比をうまく扱うこと」だから、こんな図を書いてみるよ。
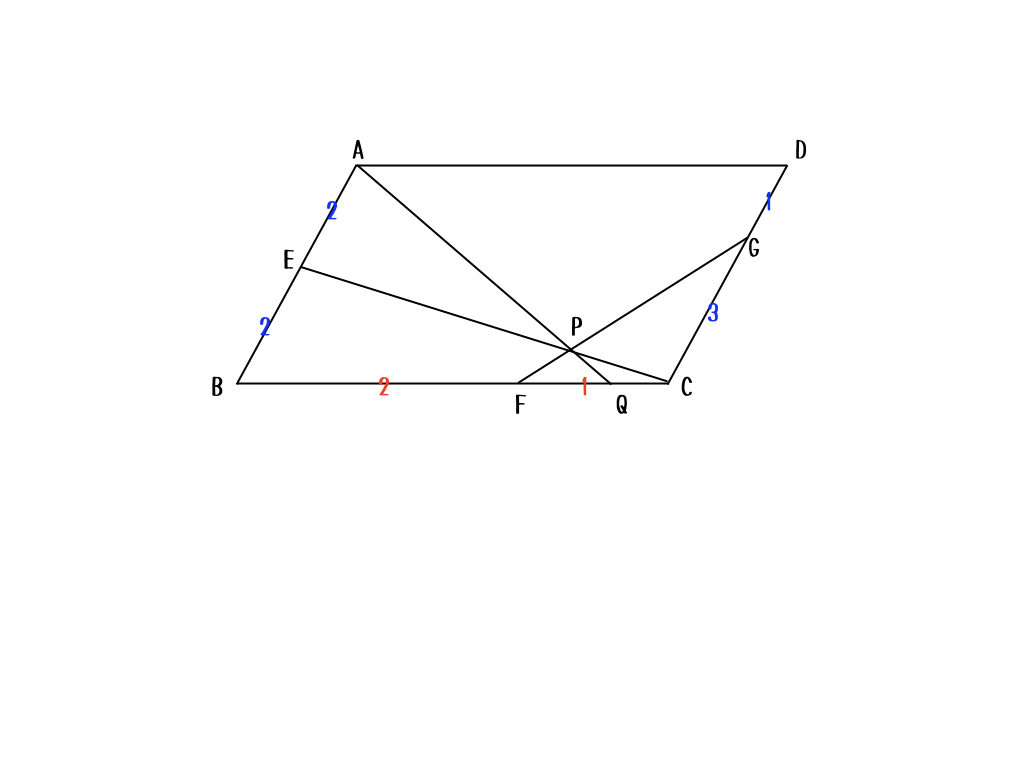
ポイントは、辺の比を合成する、ってことかな。辺\(AB\)と辺\(CD\)は同じ長さだから、比の和が同じになるように調節してあげることで、比べられるようになるからね。
なるほど。色を分けて、比較できる辺の比を見やすくしているんだね。
うん。比べられる辺の比を区別することは重要だよ。じゃあ、平行四辺形の時にしょっちゅう現れる補助線を引いてみるよ。
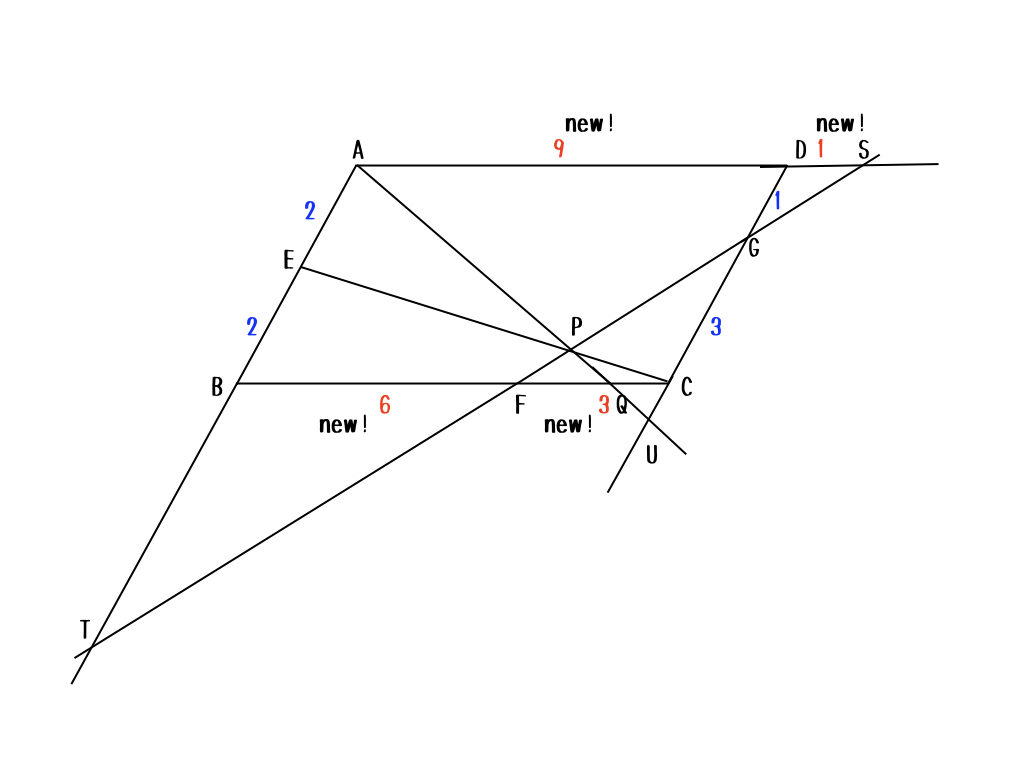
こんな感じで補助線を引くんだ。途切れている三角形を作り出す感じかな。そうすると相似な関係が使いやすくなるからね。例えば、三角形CFGと三角形DGSが相似だから、\(DS:CF=3:1\)になって、\(BF:CF = 6:3\)になるから、新たに、\(AD:DS = 9:1\)だということがわかるよね。
次は、例えば三角形DGSと三角形SATを使って、\(DG:AT = 1:10\)になるよね。だから、\(BT\)は青の6になるのかな。
正解。こんな感じ。
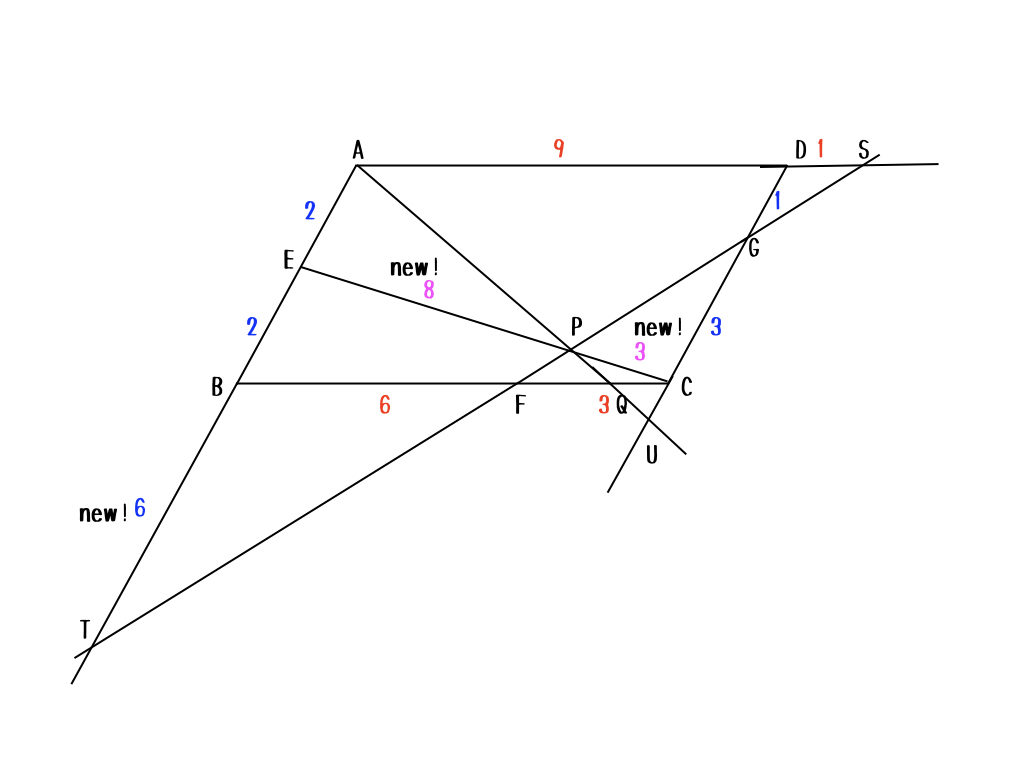
三角形CGPと三角形EPTの相似関係から、\(EP:PC = 8:3\)だね。さて、そろそろゴール地点を確認しておこっか。求めたいのは\(AP:PQ\)だから、何がわかればいい?
私は、\(AS:FQ\)を目標にしていたけど。。。
うん。それでもいいね。でも、ここはあえて、\(BQ:QC\)をもとめよっか。
え? そうなの? じゃあ、\(AB:CU\)が知りたいから、\(CU\)を求めないとダメだね。三角形AEPと三角形CPUの相似を使って、\(CU=\frac{3}{4}\)だから、\(AB:CU = BQ:QC =16:3\)かな。
いいねいいね。じゃあ、ここまでわかったね。
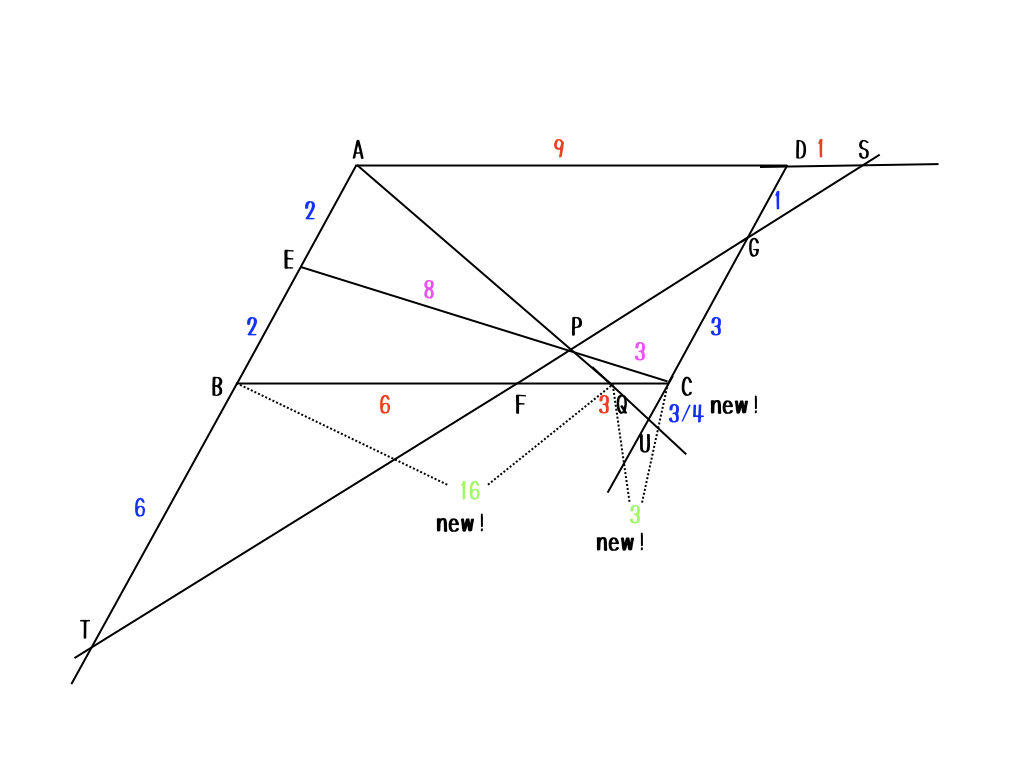
これで、\(AP:PQ\)を求める準備が整ったよ。さぁ、最後のトドメは?
ちょっと待って。私の目標と違うからなぁ。ん〜、あ〜、そうか。メネラウスの定理か。
そうだね。こうすれば見やすいかな?
これで、
$$\frac{AE}{EB}\times\frac{BC}{CQ}\times\frac{PQ}{AP} = 1$$
$$\frac{PQ}{AP} =\frac{3}{19}$$
になるから\(AP:PQ = 19:3\)ってことになるんだね。
そっか。この方法なら中学生でも解けるよね。
さぁ、じゃあ今度はベクトルで解こう。ベクトルはようこちゃんの出番だね。
ベクトルによる解法
ようこちゃんは、どういう風にベクトルを置いた?
え? 普通に、\(\overrightarrow{AB} = \vec{b}, \overrightarrow{AD} = \vec{d}\)にしたよ。
おっけい。
ベクトルだと、計算ばかりになっちゃうから、何を計算しているか見えるように図も一緒に描こうかな。
おっ、優しいね、ようこちゃん。
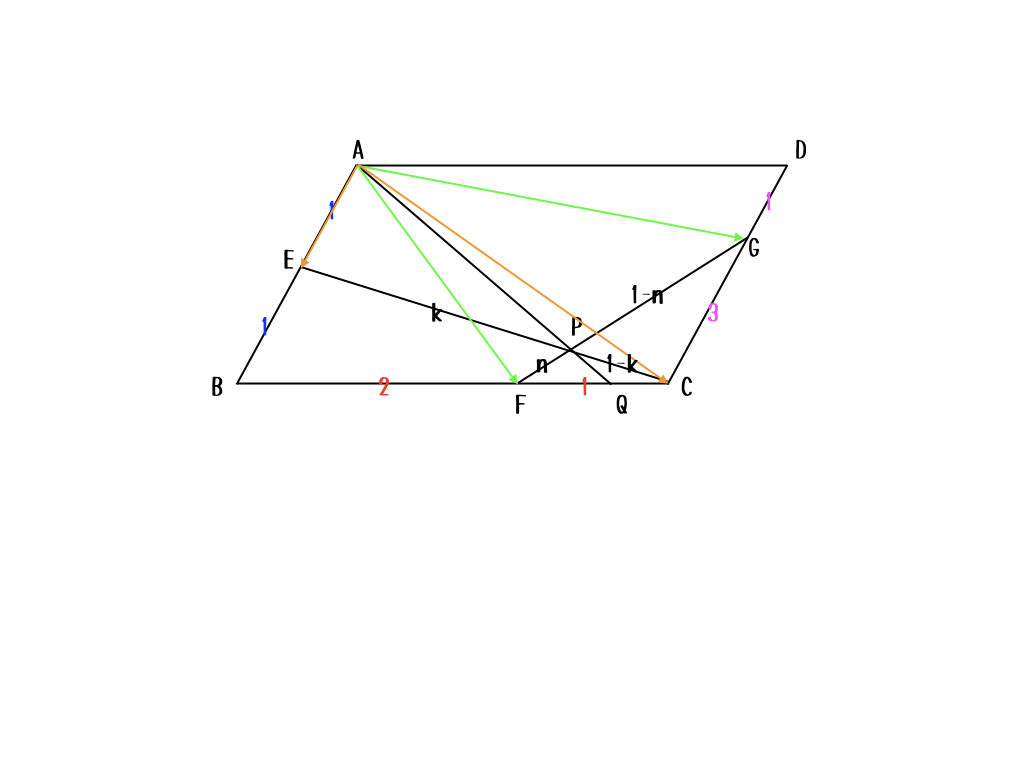
こんな感じで、\(\overrightarrow{AP}\)を2通りの方法で表して、その時に一緒に出てくる\(EP:PC\)の値を使って、さっきと同じように\(BQ:QC\)を求めた後、\(\overrightarrow{AQ}\)を求めて、\(\overrightarrow{AP}\)と比較するよ。最後は、メネラウスを使ってもいいんだけどね。
うん、方針はわかった。ベクトル、定番の方法だね。
じゃあ、計算するよ。
\(\overrightarrow{AF} = \vec{b} +\frac{2}{3}\vec{d}, \overrightarrow{AG} = \frac{1}{4}\vec{b} +\vec{d}\)を使って、緑色のベクトル二つから\(\overrightarrow{AP}\)を求める式は
$$\overrightarrow{AP} = k\overrightarrow{AG} + (1-k)\overrightarrow{AF} = \left( 1-\frac{3}{4}k \right)\vec{b} + \left (\frac{2}{3}+\frac{1}{3}k \right)\vec{d}$$
だね。それで、オレンジ色のベクトル二つから\(\overrightarrow{AP}\)を求める式は
$$\overrightarrow{AP} = n\overrightarrow{AC} + (1-n)\overrightarrow{AE} = \left( \frac{1}{2}+\frac{1}{2}n \right)\vec{b} + n\vec{d}$$
となるね。それで、この二つを係数比較する。
答案を書く時には、係数比較をするとき、\(\vec{b}, \vec{d}\)は一次独立なので、っていう言葉を書かないとね。平行四辺形だから、一次独立(互いに平行ではなく、どちらも\(\vec{0}\)ではない)なのは当たり前のことだけど、論理という意味では、この言葉を添える必要があるよ。
そうだね。じゃあ、\(\vec{b}, \vec{d}\)が一次独立なので、係数比較ができて
$$n = \frac{2}{3}+\frac{1}{3}k, \frac{1}{2}+\frac{1}{2}n = 1-\frac{3}{4}k$$
だね。これを解くと、\(k = \frac{2}{11}, n = \frac{8}{11}\)となる。ちなみに\(\overrightarrow{AP} = \frac{4}{11}\vec{b} + \frac{8}{11}\vec{d}\)と計算できる。次は、\(BQ:QC\)をメネラウスの定理で求める。注目すべき三角形はこれかな。

今出てきた\(n\)から\(EP:PC = 8:3\)だとわかるね。メネラウスの定理は
$$\frac{CQ}{QB}\times\frac{BA}{AE}\times\frac{EP}{PC} = 1$$
だから、\(BQ:QC = 16:3\)となって、初等幾何の時と同じ値になる。せっかくだから、このままベクトルで解きたい。方針としては
\(\overrightarrow{AQ} = m\overrightarrow{AP}\)という方程式を立てて\(m\)を求めれば、\(AP:AQ\)がわかるから、それを使って答えが出るね。
そのためには、\(\overrightarrow{AQ}\)を求める必要があるけどすでに、\(BQ:QC = 16:3\)がわかってるから
$$\overrightarrow{AQ} = \frac{3}{19}\vec{b} + \frac{16}{19}(\vec{b}+\vec{d}) = \vec{b} + \frac{16}{19}\vec{d}$$
と求められる。で、
\(\overrightarrow{AQ} = m\overrightarrow{AP}\)とこれらの式を使って\(m = \frac{19}{22}\)だから、最終的に答えは
\(AP:PQ = 19:3\)と同じものが出てくるね。
お見事、ようこちゃん。ベクトルはお手の物だね。
ベクトルはやり方が限られていて、あんまり頭を使わないから。係数比較をしていれば解けるって感じ。ただ、普通は高校生じゃないと解けない解法なんだけどね。
じゃあ、最後、座標平面に平面図形を置いて解く方法を紹介するよ。これは、ぶっちゃけ、ほとんど中学1年生の知識で解けちゃうから。
座標平面を応用した解法
直交座標でもできるんだけど、ここはあえて、斜交座標で考えるよ。その方が平行四辺形を置きやすいからね。斜交座標っていうのは、\(x\)軸と\(y\)軸が直角に交わっていない座標系のことだよ。こんな感じかな。

じゃ、ここからポイント。座標平面上に平面図形を置く場合、計算をできる限り簡単にするには、「どこまで具体的な数字を使って良いか」をしっかり考えることが大事だよ。
いわゆる、一般性を失わない範囲で、具体的に表すってことだね。
うん。今の場合だと、「辺の比」だけが問題になっていて、平行四辺形の形やその具体的な長さには何も条件がないよね。ということは、それらの具体的な長さを勝手に与えても、問題における一般性を失わないってことなんだ。だから、この場合、次のように座標を与えてみよう。
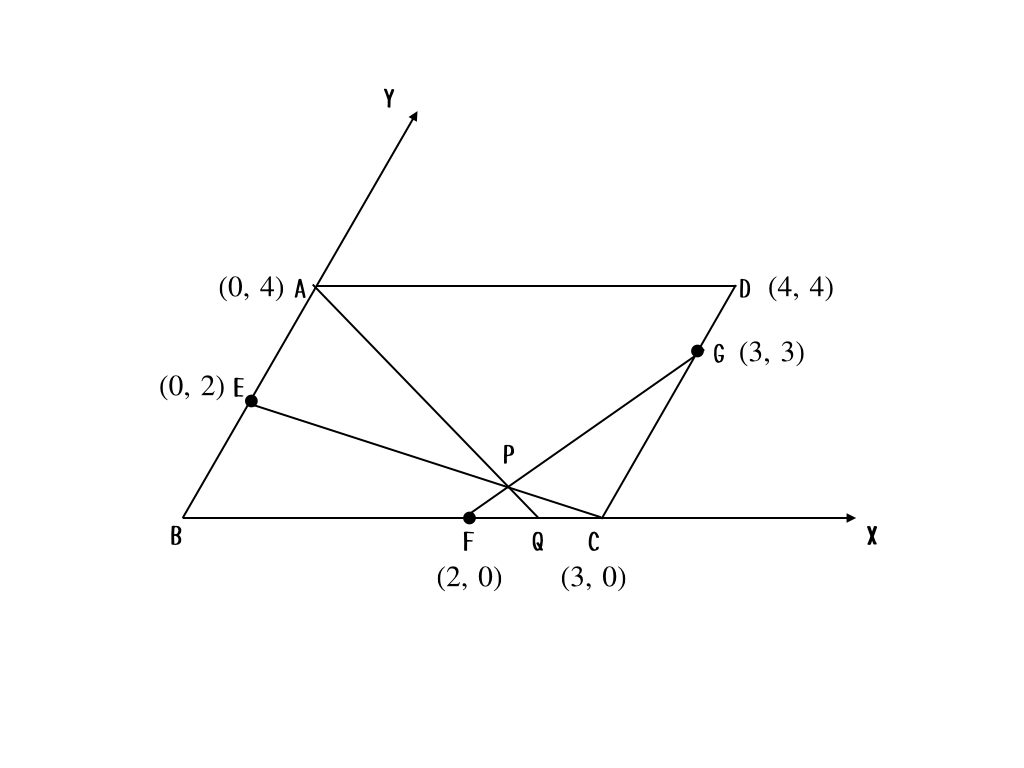
なるほど〜。つまり、一次関数の問題として解けるってことかな? 結局点Pの座標と点Qの座標を求めればいいってことだもんね。直線の式を求めて、その交点を求める問題だ。
さすが、察しがいい! 直線EC, 直線FGの式はそれぞれ
$$y = -\frac{2}{3}x + 2,\ y = 3x-2$$
と求められるから、その交点は\( \frac{24}{11},\ \frac{6}{11} \)になる。
これを用いて直線APの式を求めると
$$y = -\frac{19}{12}x+4$$
だから、点Qの\(x\)座標は\( \frac{48}{19}\)だ。
最後は点P, 点Qの\(x\)座標を比較してフィニッシュ。
$$AP : AQ = \frac{24}{11} : \frac{48}{19} = 19 : 22$$
だから、\(AP:PQ = 19:3\)だね。
いろんな解き方を一度にわかりやすく試すことができる、という点では過去問としてはすごくいい問題だよね。
そうかも。こういう感じで、平面図形を解くときには最低でもこの3つは準備して臨むのがいいかな。3つの中で得意なものがある場合は、それを主軸に考えていってもいいと思うけど、三刀流で勝負に挑めるくらい練習すれば文句ないね。ようこちゃんも、この機会にベクトル以外の解法に慣れていこうよ。
よし、じゃあ、次の問題は?
2010年甲 第3問 やり方を間違えると鬼の計算
やっぱり図が欲しいよね。いっつもようこちゃんに描いてもらっているし、今日はあたしが描こうかな。
あっ、よろしく。
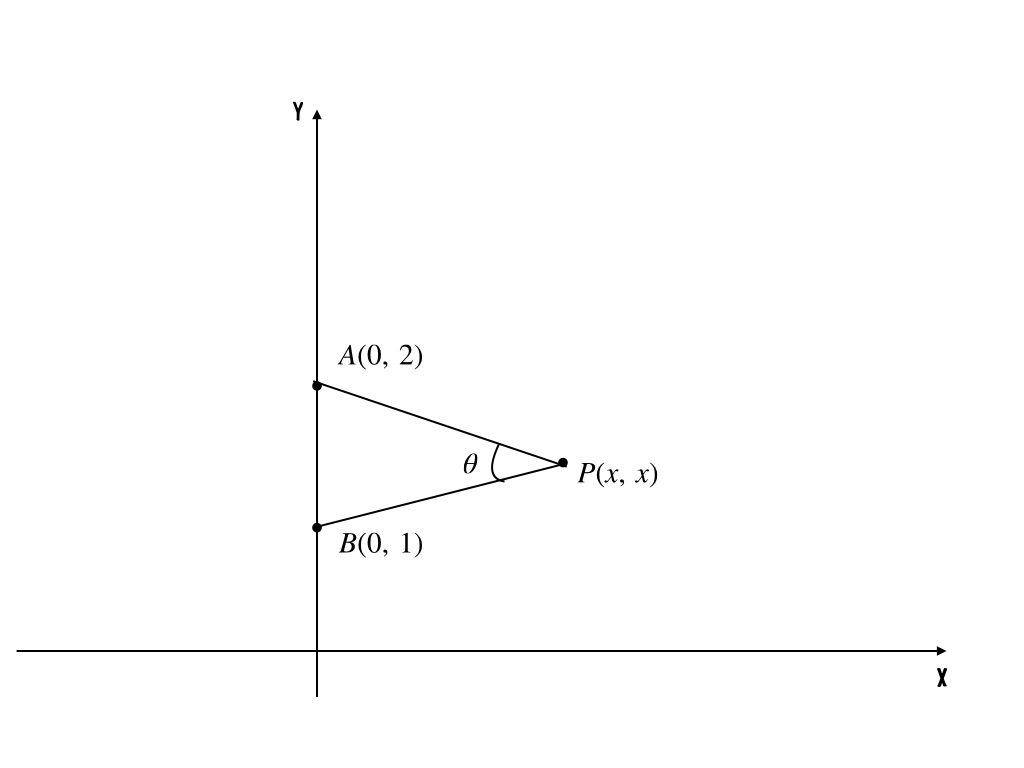
ちょっと味気ないけど、こんな感じかな。情報は十分入っていると思うけど。さて、ようこちゃん、どうやって攻める?
私なら、迷わず余弦定理だけど。
余弦定理かぁ。やってみる?
\(AP = \sqrt{x^{2} + (x-2)^{2}} = \sqrt{2x^{2}-4x+4}\)
\(BP = \sqrt{x^{2} + (x-1)^{2}} = \sqrt{2x^{2}-2x+1}\)だから
余弦定理を使うと
$$\cos{\theta} = \frac{4x^{2}-6x+4}{2(\sqrt{2x^{2}-4x+4})(\sqrt{2x^{2}-2x+1})}$$
\(\cdots\cdots\)なるほど。
続けて、続けて。
え? えと、分母・分子が正の数だから、とりあえず2乗しとくと
$$\cos^{2}{\theta} = \frac{(2x^{2}-3x+2)^{2}}{(2x^{2}-2x+1)(2x^{2}-4x+4)}$$
って感じで、\(\theta\)を最大にするには\(\cos^{2}{\theta}\)を最小にするから、微分? これを?
おっ、ようこちゃん、気合い入ってるね。これを微分しようとは。
違うでしょ。微分したくないから戸惑ってるんじゃない。
あ、微分しない? それでもできるんだけどなぁ。
その意地悪モード、そろそろ止めようよ。時間と心のゆとりがあればできるかもしれないけど、これを微分するのはとてもじゃないけど、やりたくないよ。
そっか。でも、実際の計算は5次式までの整数係数の多項式の計算だから、気合いと根性で乗り越えられるけどね。
私は気合いも根性もないからさ、別の方法を考えたいなぁ。
了解! ちなみに、一生懸命頑張って計算すると
$$f^{\prime}(x) = (\cos^{2}{x})^{\prime} = \frac{2x(x^{2}-1)}{(2x^{2}-2x+1)^{2}(2x^{2}-4x+4)^{2}}$$
になるよ。
まみ、これ計算したの?
え、まぁね。あたしはこういう、ガリガリした計算好きだからさ。ちなみに、ようこちゃん、別の方法を考えるって、いってたけど、どうする? 余弦定理を使う前に戻るってことかな?
そうだね。せっかく座標平面上にあるんだから、何か別の方法を考えたいよ。
うん。座標平面においてあったら、コサインよりももっと別のものの方が相性がいいもんね。
あ、そうか。タンジェントだ。直線の傾きはタンジェントで表せるんだったね。とすると、こんな感じで補助線を引くのがいいのかな?
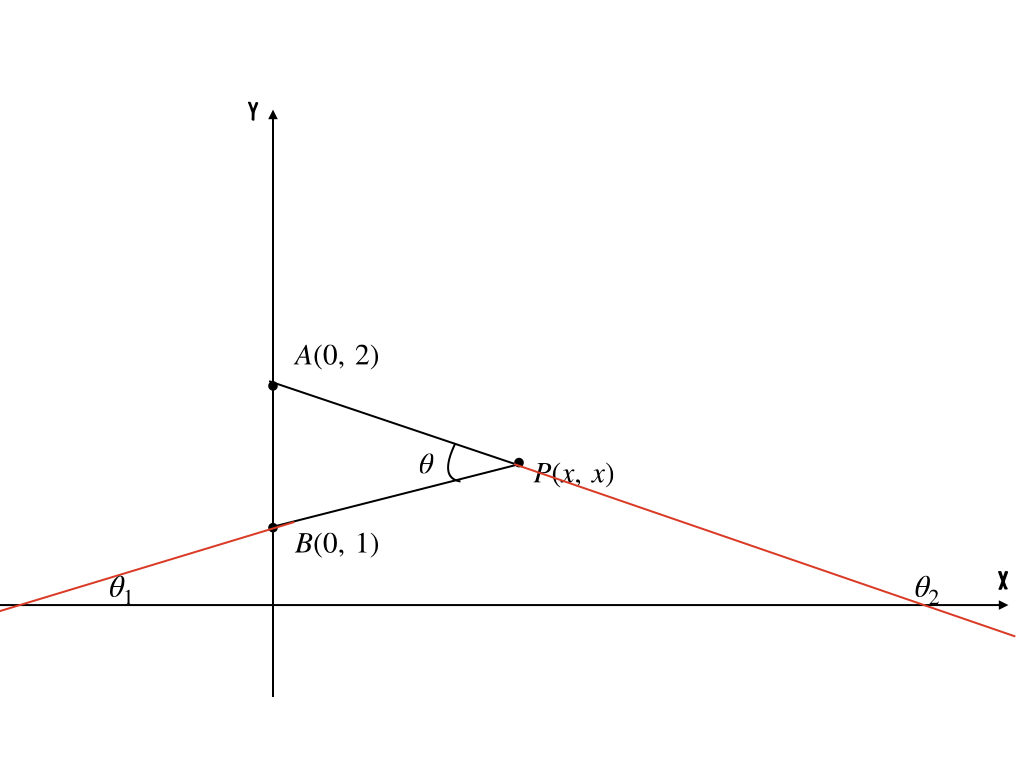
うん、そうだね! ただ、これは\(x < 2\)の時の場合だから、\(x > 2\)の場合も描いておいたほうがいいかも。
こんな感じかな。

うん。バッチリ。じゃあ、それぞれの場合で\(\theta\)を求める式を導出してみよう。
まず\(x < 2\)の場合ね。
\(\theta = (\theta_{1} + (\pi-\theta_{2}))\)だから、両辺にタンジェントをとると
$$\tan{\theta} = \tan{(\theta_{1} + (\pi-\theta_{2}))}$$
ていう感じになって、タンジェントの加法定理を使うと
$$\tan{\theta} = \frac{\tan{\theta_{1}} + \tan{(\pi-\theta_{2})}}{1-\tan{\theta_{1}\cdot\tan{(\pi-\theta_{2})}}} = \frac{\tan{\theta_{1}} – \tan{\theta_{2}}}{1+\tan{\theta_{1}\cdot\tan{\theta_{2}}}} $$
だね。あとは、直線の傾きとタンジェントの関係性で
$$\tan{\theta_{1} = \frac{x-1}{x}}, \tan{\theta_{2} = \frac{x-2}{x}}$$
だから、これを代入すると
$$\tan{\theta} = \frac{x}{2x^{2}-3x+2}$$
となる。わぁ、さっきのに比べたら、すごく簡単になった。
そうなんだよ。ちなみに、\(x>2\)の場合はどうだろう?
同じように考えると
\(\theta = \theta_{1} – \theta_{2}\)だから
$$\tan{\theta} = \tan{(\theta_{1}-\theta_{2})}$$
で、加法定理を使って
$$\tan{\theta} = \frac{\tan{\theta_{1}}-\tan{\theta_{2}}}{1+\tan{\theta_{1}}\cdot\tan{\theta_{2}}}$$
だから、代入して、ってあれ? 同じ式じゃん。
実はね、どっちの場合も同じ式になるんだよ。ちなみに、この式って\(x=2\)でも成り立つ式だよね。だから、\(x > 0\)の範囲内で一般に成り立つ式だよ。
それは、助かる! じゃあ、この式の最大値を出せばいいんだ。つまり、び
微分しようと思ってない? ようこちゃん。
思ってるよ。だって、それで解けそうじゃん。
もちろん。でも、ここはもう少し簡単に計算する方法があるよ。こんな感じにしたら気づくかな?
$$\tan{\theta} = \frac{1}{2x-3+\frac{2}{x}}$$
あ〜、相加・相乗平均かぁ。
うん。文系の学生の場合は、分数関数の微分は習っていないけど、こういう風にすれば最大値、求められるよね。
分母の最小値を求めれば、全体として最大になるからだね。\(x > 0\)だから
$$2x + \frac{2}{x} \leq 2\sqrt{4} = 4$$
と計算できて
$$\tan{\theta} \leq \frac{1}{1} = 1$$
だから、\(\theta\)の最大値は\(\frac{\pi}{4}\)つまり、\(45^{\circ}\)だね。
そういうこと。難しい入試問題で求められる”計算能力”っていうのは、複雑な計算を正確に計算することだけじゃなくて、”いかに計算ミスが減る道筋を発見できるか”っていうことも含まれてて、どれだけ頭を使って目の前の計算をしているか、ってことなんだと思うよ。
う〜ん。悔しいけど、否定できないな。私はちょっと気をつけないとね。
なんて、偉そうなこと言っているけど、あたしはあんまり頭使わないで、ガリガリ計算しちゃんだけどね。
さっきの微分の計算みたいに? でもそれで正しい答えにたどり着くんだから、やっぱりすごいよ。
え? そうかなぁ。ようこちゃんに褒められると嬉しい。
照れてないで、次の問題出してよ。
そうだなぁ、次はこれにしようかな。
2008年甲 第3問 幾何の魅力
最初に言っちゃうけど、今回、計算は0で答えを出そうよ。
え? なにその縛り。
この図だけで勝負しようよ。

計算ゼロか。じゃあ、ベクトルはダメだね。
もちろん。これは初等幾何で解いてこそ、っていう問題だよ。
補助線もいらないのかな?
いらないよ。本当に、この図だけ、じっくり見て、たった2つの幾何の知識を組み合わせればあっという間に答えが出てくるよ。
おっけい。ちょっと黙って考えていい?
いいよ。ようこちゃん、やる気満々だね。じゃあ、あたしはその間に数学オリンピック(日本本戦)の幾何の問題を解いているよ。
え? それも興味あるなぁ、いや、ちょっと集中しなきゃ。
(おまけ)数学オリンピック日本本戦 2003年 第1問
\(AR = RB = CP\)かつ\(CQ = PQ\)
であるとき、\(\angle BRC\)の大きさを求めよ。ただし、2点\(X, Y\)に対し、線分\(XY\)の長さを\(XY\)で表している。
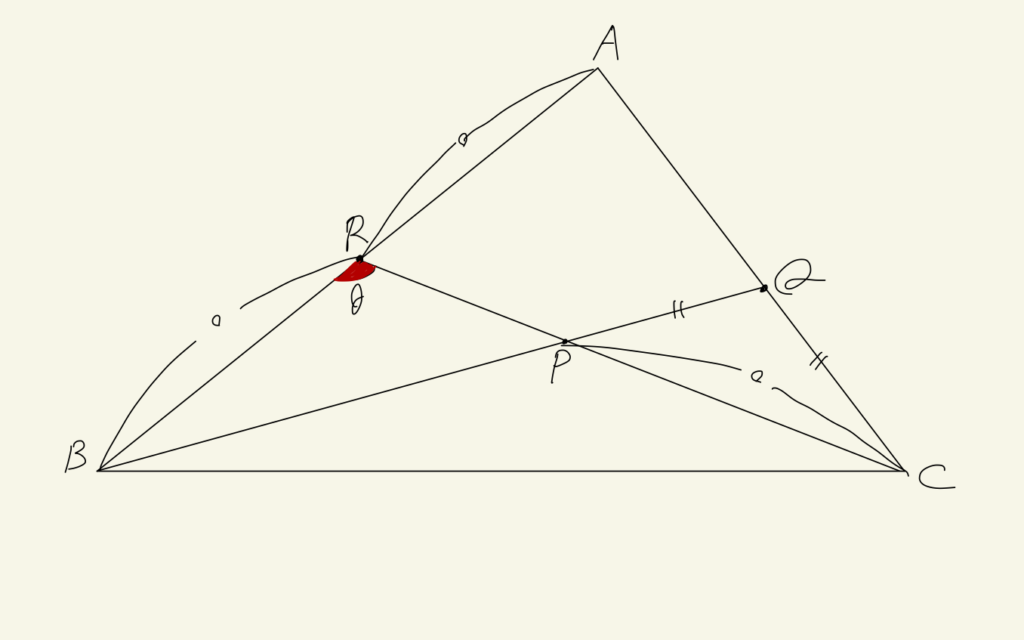
取り組みようがないような問題に見えるけど、まずはメネラウスの定理を使ってみるのが鍵。
$$\frac{RA}{BR}\cdot\frac{CQ}{AC}\cdot\frac{PB}{PQ} = 1$$
すると、うまいこと等しい辺が見つかるので
$$PB = AC$$
が出てくる。この後、少し次の手に困るけど、ポイントは補助線。
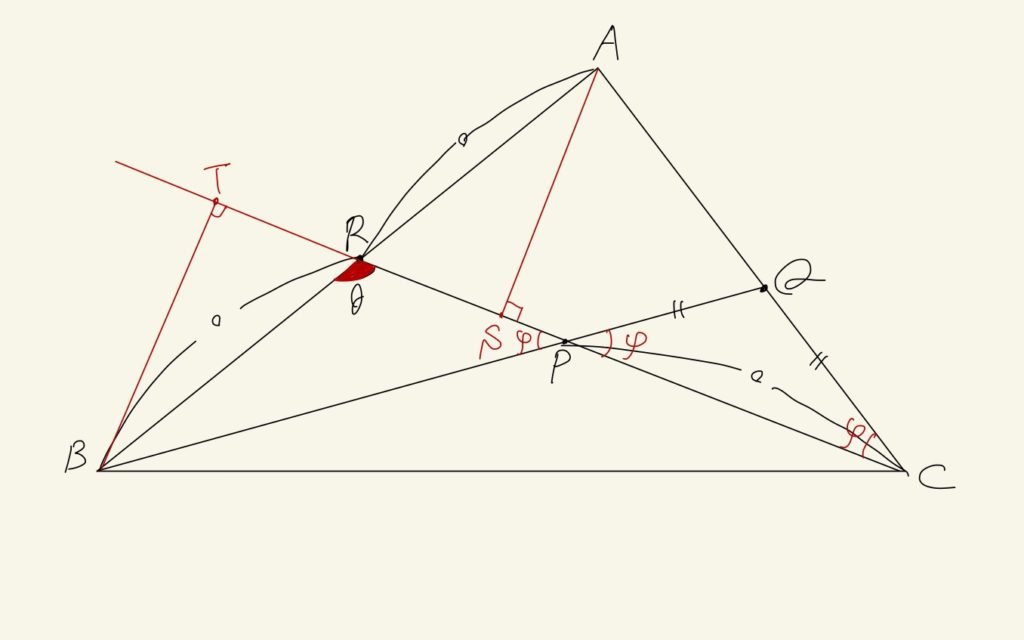
こんな補助線が引けたら、あとは次の関係に気づくかどうか。
$$CS = AC\cos{\psi} = PB\cos{\psi} = TP$$
ここまで行くとあと一歩。
続きはこちらの記事で。
まみ、わかった! 今、すごくスッキリした。
あ、ようこちゃん。できた?
できたよ! 本当に計算いらずでできたよ。
へ〜、じゃあ、教えてよ。
うん。聞いて聞いて。確かに2つ、幾何の知識を組み合わせればいいけど、どっちも珍しい使い方するね。
1つ目は、相似。相似ってほとんど2つの角度が等しいっていう条件で証明するけど、今回は二辺の比とその間の角が等しいっていうレアな条件だったね。
うんうん、どこが相似だった?
三角形\(ACM\)と三角形\(ANC\)でしょ。そうすると
$$MC : CN = 1 : 2$$
という比の関係が出てくる。で、次が問題だよね。普通はしない使い方。
ためるね、ようこちゃん。
え? じゃあ、言うよ。角の二等分線と二辺の比の関係。こんな定理。
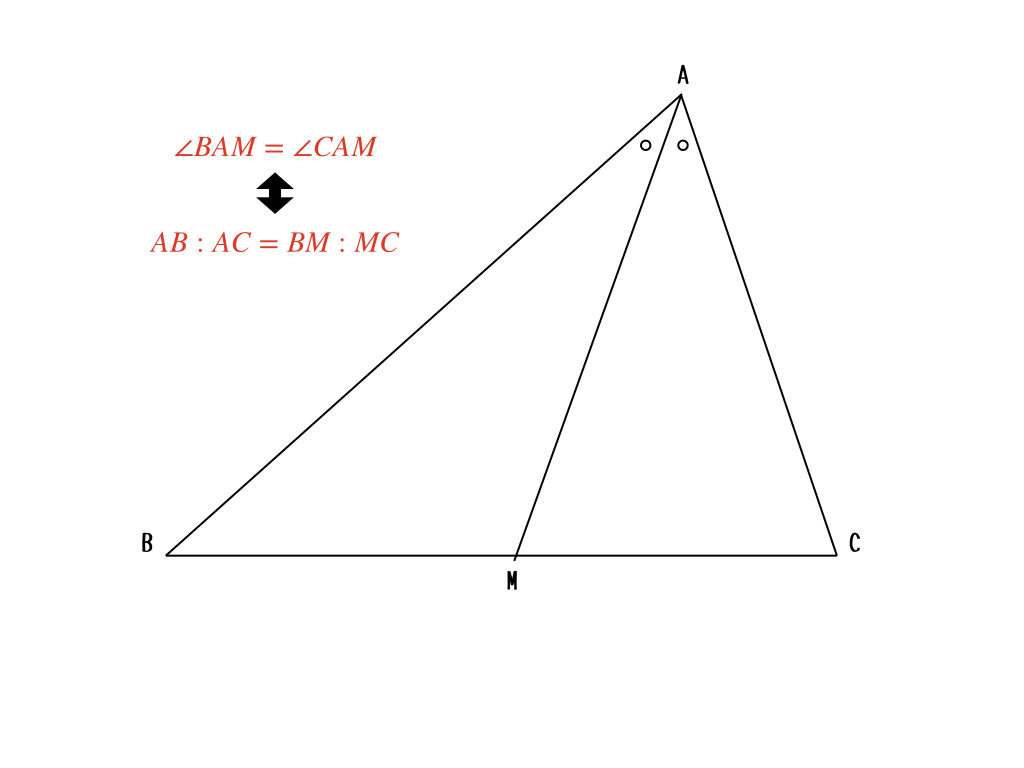
上から下はよく使うけど、下から上にはなかなかいかないよね。でもこの問題の場合、ちょうど
$$CM:CN = NB:BN = 1 : 2$$
になっているからこの定理の逆が使えて、\(\angle BCM = \angle BCN\)が証明できちゃうんだ。
ようこちゃん、大正解! うん、まさにそういうことだったよ。他にも証明する方法はたくさんあるけど、これがスマートだよね。それにスッキリするし。
うん、確かにスッキリした。
このスッキリする感じが初等幾何の醍醐味でね。ベクトルとか座標平面に置いちゃうと、無味乾燥でしょ。その分計算問題に落とし込めるからいいんだけど、時間があるときは幾何で鮮やかに解いてみるのも楽しいと思うよ。
まぁ、こういうのは楽しいかなぁ。
じゃあ、次はこんなのどうだろう。
1969年 第2問 オッカムのカミソリ
$$\tan{\alpha}\cdot\tan{\beta} = \frac{△ADB}{△ACB} = \frac{DP}{CP}$$
ポイントは、必要以上に多くの情報を導かないことだよ。と言ってもこれが一番難しいことかもしれないんだけどね。何が必要か、何が答えに直結するかは最初はわからないもんね。
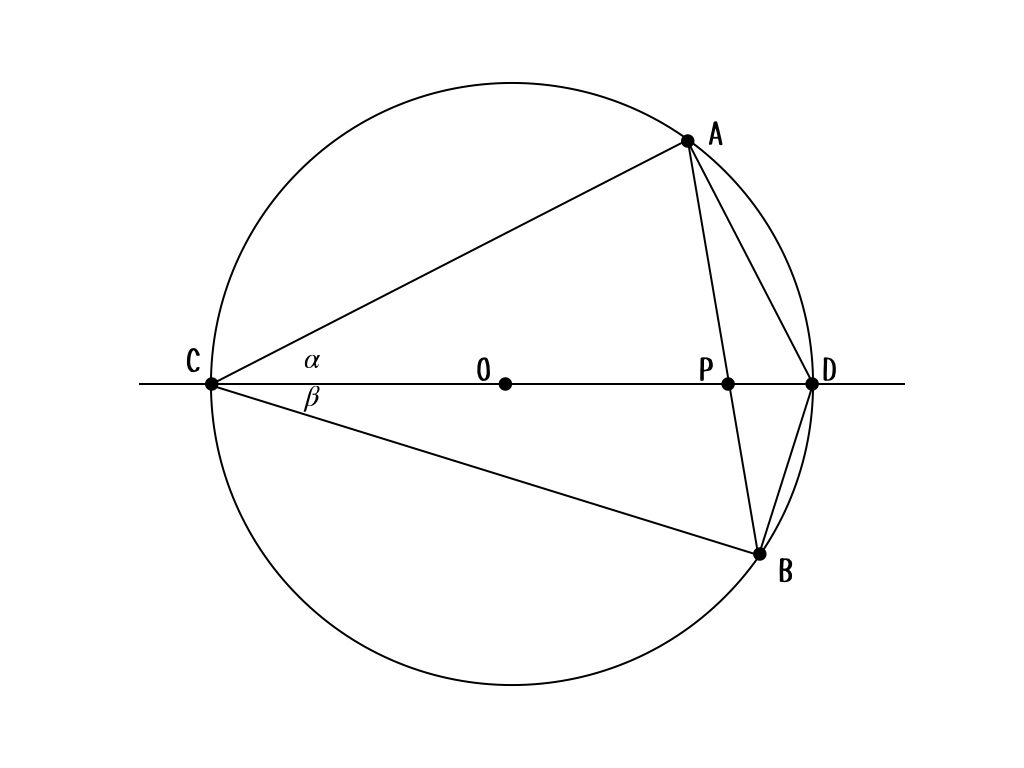
後半の証明、面積の関係と辺の長さは有名だね。\(AB\)はどちらの三角形においても底辺になっていて、それを共有しているから、高さと対応している辺同士が面積の比になっているっていう。
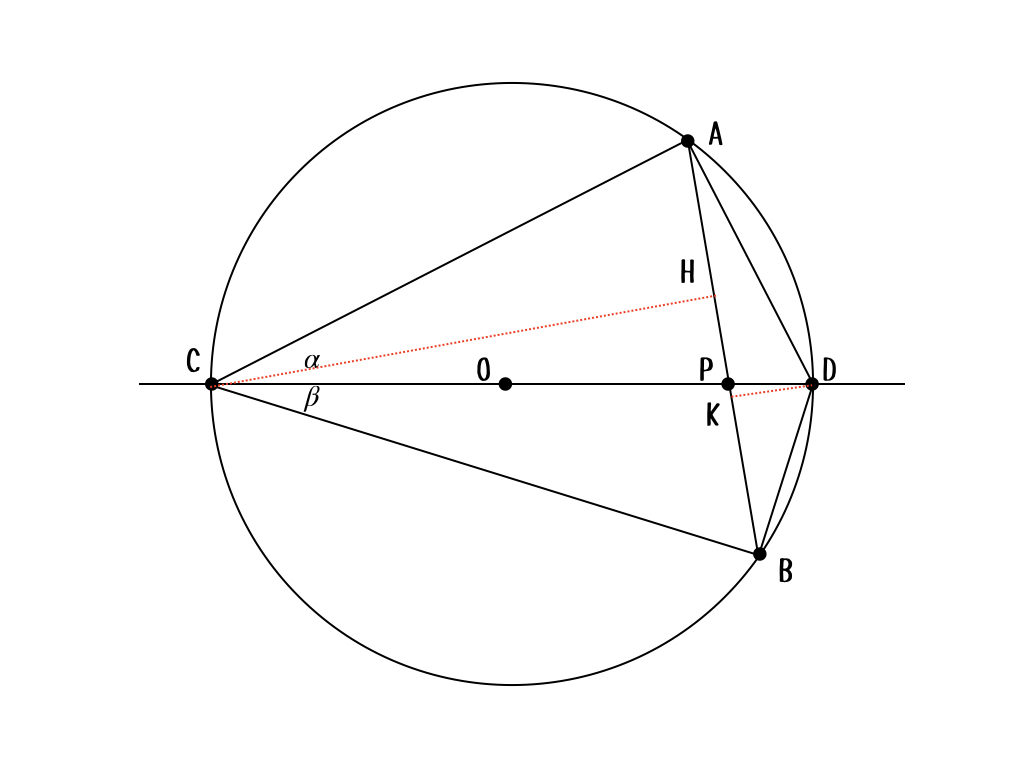
こういう補助線を引くとわかりやすいかな。赤い線は高さね。このとき
$$CH : DK = CP : DP$$
が成り立つから、面積比は
$$\frac{△ADB}{△ACB} = \frac{DP}{CP}$$
だよね。
そうだね。ポイントは前半をどうやって証明するかだけど。
私、まだ慣れてないから、例えば\(CD = 1\)と仮定して\(\angle CAD = 90^{\circ}, \angle CBD = 90^{\circ}\)ということから、\(AC, AD, CB, BD\)を\(\cos{\alpha}, \sin{\alpha}, \cos{\beta}, \sin{\beta}\)と表して計算したくなるんだけど、多分、違うんでしょ?
いやいや、いいと思うよ。辺の長さを仮定しても、一般性は失わないからね。問題はそこからどう発展していくか、だけど。
う〜ん。式をみると\(\tan\)があるから、こんな補助線を引いて\(\tan{\alpha}\)とかを見やすくしたいんだけど。
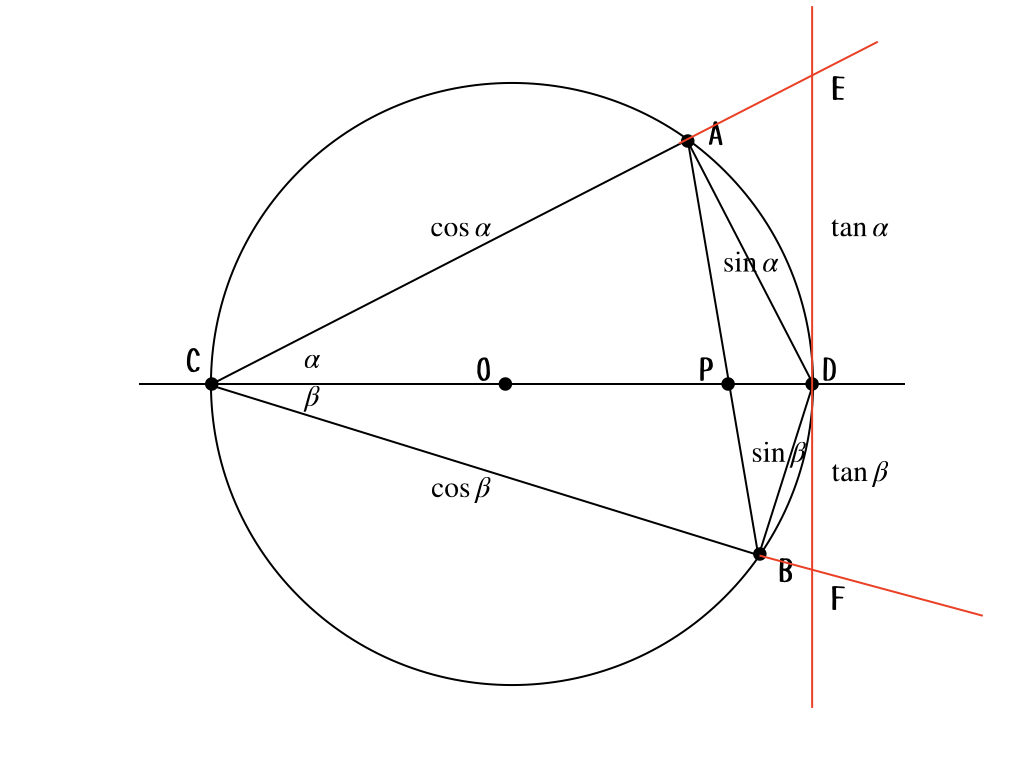
お〜、確かにそうなんだけど、いまいち、使いにくくない? 実は、タンジェントを一旦忘れて、それぞれの三角形の面積を求めることに集中した方が近づいていくと思うよ。ようこちゃんのファインプレーのおかげで、準備はほとんど整っているんだけどなぁ。
2つの三角形の面積? \(△ACB, △ADB\)のこと? 確かに片方はすぐに求められるけど。反対側の角度は。
ようこちゃん、この四角形、ただの四角形じゃないよ。
ん〜、円に内接する四角形だよね。あ、そうか、反対側の角度は\(180^{\circ}\)から引いたものになっているんだっけ? なら\(\angle ADB = 180^{\circ}-(\alpha+\beta)\)なんだ。それなら、2つの三角形の面積が求められそうだよ。
$$△ACB = \frac{1}{2}\cos{\alpha}\cos{\beta}\sin{(\alpha+\beta)}$$
$$△ADB = \frac{1}{2}\sin{\alpha}\sin{\beta}\sin{(180^{\circ}-(\alpha+\beta))}$$
それで、\(\sin{(180^{\circ}-(\alpha+\beta))} = \sin{(\alpha+\beta)}\)だから
$$\frac{△ADB}{△ACB} = \frac{\sin{\alpha}\sin{\beta}}{\cos{\alpha}\cos{\beta}} = \tan{\alpha}\tan{\beta}$$
となって、証明終了!
うん、いい感じ。初等幾何で大事なのは、パワフルな計算よりも繊細な視野だからね。じゃあ、次はようこちゃんのお家芸、ベクトルの問題にしよう。
1992年 第3問 ピタゴラスが見えるか?
\(△ABC\)の外心\(O\)から直線\(BC, CA, AB\)に下ろした垂線の足をそれぞれ\(P, Q, R\)とするとき、\(\overrightarrow{OP} + 2\overrightarrow{OQ} + 3\overrightarrow{OR} = \vec{0}\)が成立しているとする。
(1)\(\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}\)の関係式を求めよ。
(2)\(\angle A\)の大きさを求めよ。
ベクトルの問題は、計算だけで全て突破するって考えることもできるけど、時には計算からわかることを図に表して考えていくことも大事だよね。
この問題はどこかで見たことあるなぁ。
問題集とかに載っているかもね。ベクトルの扱い方を確認する上では役にたつ問題だからね。

図はこんな感じか。前に進むためには、\(R, Q, P\)の幾何的な意味を考える必要があるね。中心からの垂線だと、ちょうど辺の中点に位置するっていうのが重要かな。だから
$$\overrightarrow{OR} = \frac{1}{2}\left( \overrightarrow{OA} + \overrightarrow{OB}\right), \overrightarrow{OQ} = \frac{1}{2}\left( \overrightarrow{OA} + \overrightarrow{OC}\right), \overrightarrow{OP} = \frac{1}{2}\left( \overrightarrow{OB} + \overrightarrow{OC}\right)$$
が成り立つんだね。で、これを問題の等式に代入すれば(1)は解決。答えは
$$5\overrightarrow{OA} + 4\overrightarrow{OB} + 3\overrightarrow{OC} = \vec{0}$$
になる。
ようこちゃん、ベクトルは無双だね。じゃあ、(2)もどうぞ!
(2)は、(1)で求めたベクトル方程式をどうやって使うかが問題だからね。この式をパッと見ると、三平方の定理が思いつくよね。係数だけ見ると有名な比になってる。それって偶然じゃなくて、ちゃんとそうなるように問題を作っているんだよね。だから、こっちもそれを活かして解いてあげよう。ってことで
$$5\overrightarrow{OA} = – 4\overrightarrow{OB} – 3\overrightarrow{OC}$$
こうやって移項するのが筋っぽい。三平方の定理をあぶり出すために、全体を二乗すると
$$25|\overrightarrow{OA}|^{2} = 16|\overrightarrow{OB}|^{2} + 9|\overrightarrow{OC}|^{2} + 24\overrightarrow{OB}\cdot\overrightarrow{OC}$$
ってなる。ポイントは半径はどれも等しいってことで結局
$$\overrightarrow{OB}\cdot\overrightarrow{OC} = 0$$
が出てくる。これって、辺\(OB\)と辺\(OC\)が直交していることを意味するから、\(\angle BOC = 90^{\circ}\)。最後に、この結果を図と照らし合わせて円周角の性質から\(\angle A = 45^{\circ}\)だね。
かんぺき! 最後に円周角を使って求められるってところが面白い工夫だと思う。ベクトルに三平方の比が入ってきたり、やっぱり、面白い問題を作るなぁ、って気がするね。
うん。だから、類題も含めていろんな問題集に使われているんだね。
そういえば、面白いっていえば、これも違う意味で面白いかも。簡単そうに見えるけど、実は奥が深いって問題。
1998年 第1問 楽勝……あれ? 解けない?
直角三角形に半径\(r\)の円が内接していて、三角形の3辺の長さの和と円の直径との和が\(2\)となっている。このとき以下の問に答えよ。
(1) この三角形の斜辺の長さを\(r\)で表せ。
(2) \(r\)の値が問題の条件を満たしながら変化するとき、この三角形の面積の最大値を求めよ。
簡単そうに見えるけど、何かからくりがあるんだよね。ま、何はともあれ図を描くか。
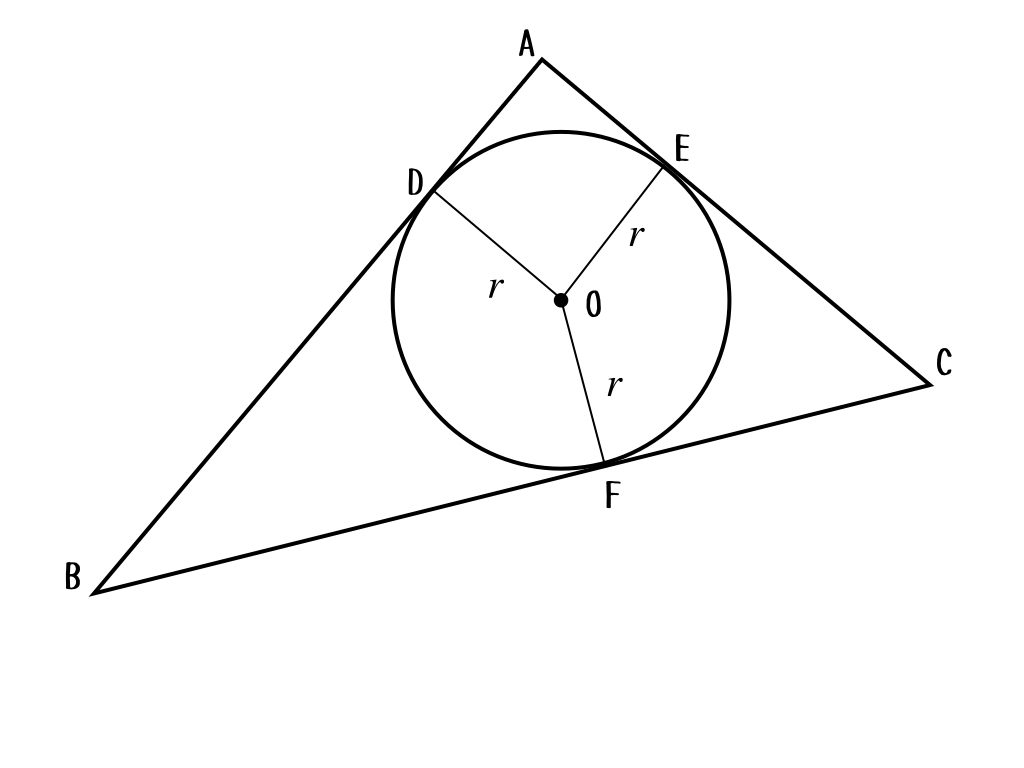
三角形の内接円といえば、面白い性質があったよね。それを使ってパラメータを決めていく?
ああ、中学数学でよくやるやつだよね。円外の一点と接点を結ぶ2つの線分の長さが等しいっていう。それを使うと、こんな感じかな。
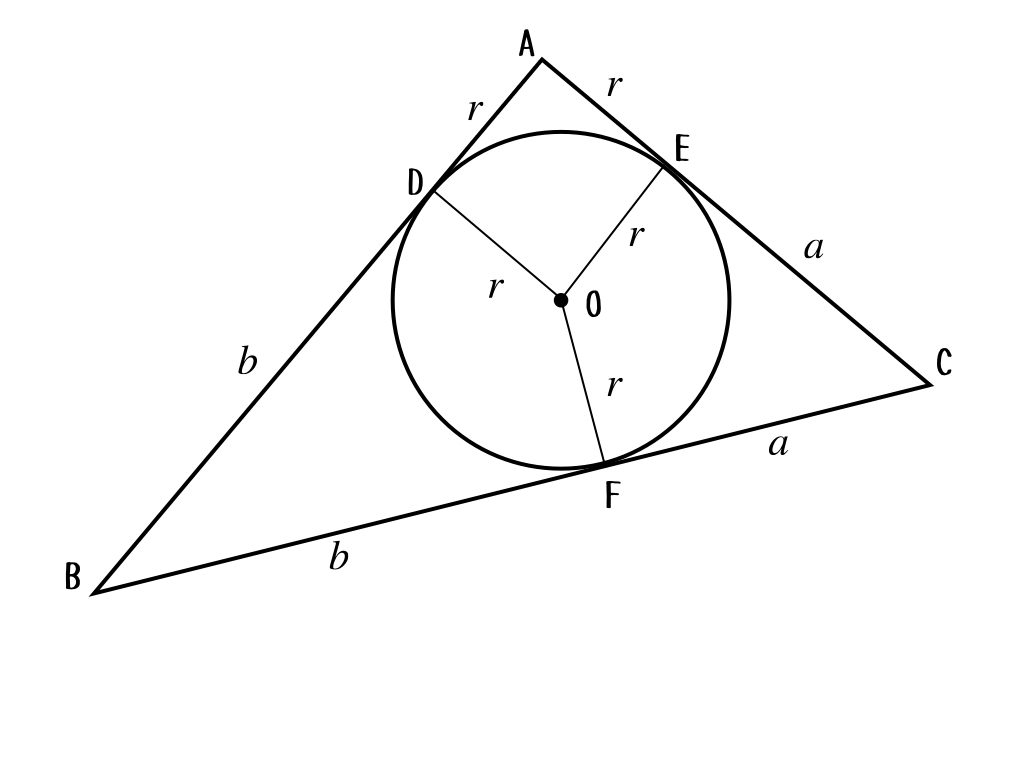
いいね。ようこちゃんは、その線分の長さをパラメータにおいたんだね。そうすると、斜辺の長さは\(a+b\)だ。これで、問題の条件を1つ使えるようになったね。
三角形の周の長さの和と直径の和が\(2\)になっているという条件だ。
$$2(r+a+b)+2r = 2$$
だから、求めたい斜辺の長さは\(a+b = 1-2r\)
と求められるね。
うん。これで(1)は終了。じゃ、次は(2)に移ろうか。
三角形の面積\(S\)は
$$S = \frac{1}{2}(a+r)(b+r) = \frac{1}{2}(ab+(a+b)r+r^{2})$$
で、\(a+b\)はわかっているんだから、あとは\(ab\)だけを求めればいいかな。多分、三平方の定理を使って\(ab\)は出てくると思うんだけど、どうだろう?
うん。いいんじゃない。やってみたら。
ちょっと怪しいけど、やってみるか。
\( (a+r)^{2}+(b+r)^{2} = (a+b)^{2} \)
\( a^{2}+2ar+r^{2} + b^{2}+2br+r^{2} = a^{2}+b^{2}+2ab \)
\(2ab = 2r(a+b)+2r^{2} = 2r(1-2r)+2r^{2} = 2r-2r^{2}\)
\(ab = r-r^{2}\)
あっ出た。
ふむふむ。あっていると思うよ。
じゃあ、あとはこれを面積\(S\)の式に代入して
$$S = \frac{1}{2}(r-r^{2}+(1-2r)r+r^{2})$$
$$S = \frac{1}{2}(2r-2r^{2}) = -r^{2}+r$$
だね。ってことは
$$S = -\left(r-\frac{1}{2}\right)^{2} + \frac{1}{4}$$
だから、\(r = \frac{1}{2}\)の時に、最大値\(\frac{1}{4}\)、かな。
第1問ってこともあって、これで満足した受験生は何人いただろうね? これが答えだったら、この問題は簡単だったはず。さぁ、ようこちゃん。なんか違和感がないかな?
そういえば、\(r= \frac{1}{2}\)だと、斜辺の長さが、、、\(0\)になってるんじゃん。じゃ、ダメじゃん。
うん、そこだよね。この問題、かなり巧妙で、どんな\(r\)でもいいってわけじゃないんだ。問題文にも”\(r\)を問題の条件を動かしながら変化するとき”としか書いてないから、\(r\)の範囲にまで頭が回らないかもしれない。実際、\(0<r<\frac{1}{2}\)だったらなんでもいいってわけでもないんだよ。
確かに、少なくとも斜辺の長さは円の直径、\(2r\)よりは大きいもんね。
さぁ、ここが勝負所だね。京大に合格するか否かの分かれ道。\(r\)の範囲を決定づける条件はなんだろう?
\(r\)の範囲か。つまり、問題文の条件、が存在すればいいんだよね。ってことは、\(a, b\)の値がそれぞれ正の値で存在すればいいってことなんだけど。ん? 2つの値が正の値で存在する条件、、、。
あ、ようこちゃん、なんかいいことに気づいたっぽいね。
\(a+b = 1-2r, ab = r-r^{2}\)なんだよ。これは実数解の存在条件が使えるんじゃないかな。だから
$$x^{2} -(1-2r)x + r-r^{2} = 0$$
という二次方程式が2つの正の解を持つような\(r\)が、問題の条件を満たす\(r\)の条件なんだ。この二次方程式の解が\(a, b\)だからね。
お見事、ようこちゃん。この条件の確認が難関大でよく”隠れて”出題されるものなんだ。自分でパラメータを設定して問題を解くとき、この確認を怠って失敗することがあるから、注意しないと。
見事と言っても、最初私は気づかなかったんだけどね。じゃあ、実際にこの条件を調べてみるよ。2数の数がともに正の実数になるような条件は方程式の解(\(\alpha, \beta\))と係数の関係を使って
$$D \geq 0,\ \alpha+\beta > 0,\ \alpha\beta >0$$
とするのが簡単かな。1つ目の条件から
\(D = (1-2r)^{2}-4(r-r^{2}) = 8r^{2}-8r+1 \geq 0\)だから
$$r \geq \frac{2-\sqrt{2}}{4},\ r \leq \frac{2+\sqrt{2}}{4}$$
2つ目の条件から
\(\alpha+\beta = 1-2r > 0\)だから
$$r < \frac{1}{2}$$
3つ目の条件から
\(\alpha\beta = r-r^{2} = -r(r-1) > 0\)だから
$$0<r<1$$
だね。ちなみに、\(\frac{2-\sqrt{2}}{4} < \frac{1}{2}\)だ。ってことは結局
$$0 < r \leq \frac{2-\sqrt{2}}{4} $$
を満たせばいいってことだね。\(r\)はこの条件を満たしながら動く。
うん。そうすると面積の最大値は何かな?
う〜んと、一応図を書くとこうなってる。
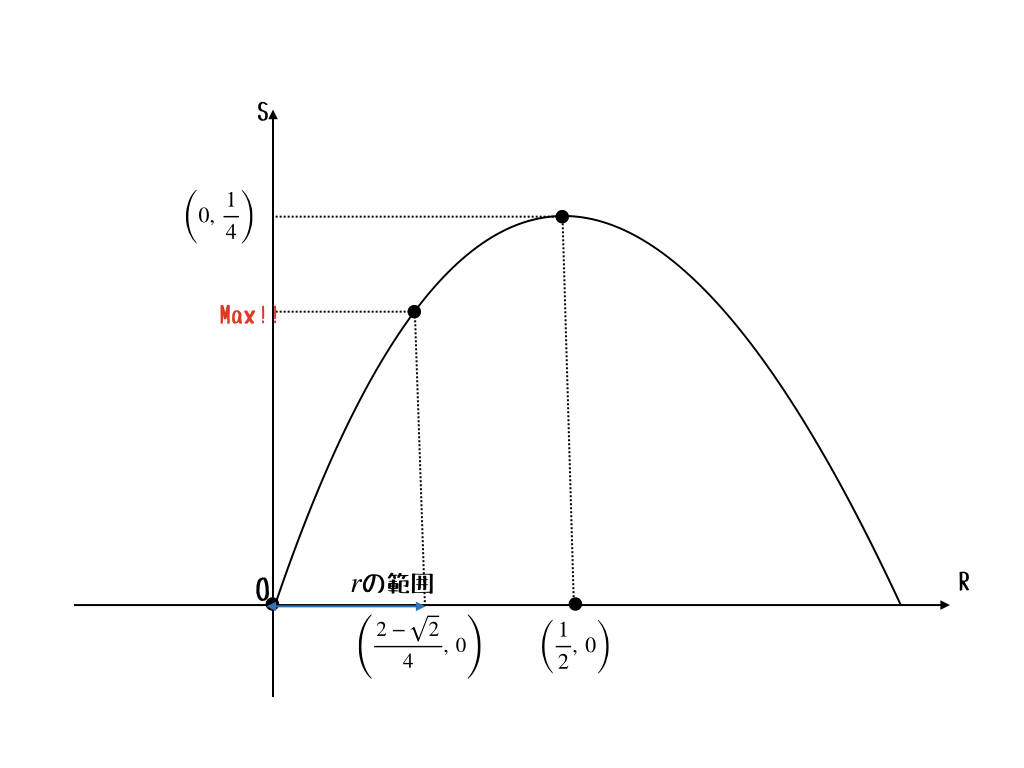
だから、\(r_{0} = \frac{2\sqrt{2}}{4}\)のときに最大だね。これを\(S\)に代入するかぁ。
ようこちゃん、”計算能力”の見せ所だよ。この意味は?
わかってるよ。
計算能力とは、複雑な計算を正確に計算することだけじゃなくて、”いかに計算ミスが減る道筋を発見できるか”のことである。
Mami ‘s statement in this article
ってことで、なるべく簡単に計算したいけど、定番の方法はあれかな? \(r\)の満たす方程式から次数を減らすって計算方法があったね。今の場合最大値を与える\(r_{0}\)は
$$8r_{0}^{2}-8r_{0}+1 = 0,\ -r_{0}^{2}+r_{0} = \frac{1}{8}$$
を満たしているわけだから、求めたい面積\(S\)は
$$S = -r_{0}^{2}+r_{0} = \frac{1}{8}$$
って、次数が2つ減って、答えが出てきた! 代入する必要なかったんだ。
正解。この計算方法が大事だよ。問題集でも次数下げで計算する問題は載っているけど、そういう問題が出たときだけこのテクニックを使うんじゃなくて、使える場面を自分で察知して計算する力を身につけないとね。
勉強になります。
さて、ようこちゃん。平面図形の難問の1つに、”3点が一直線上になることの証明”があるよね。一直線上の証明は例えばメネラウスの定理が使えるときがあるけど、かなり状況が限定されてる。それが使えないときは、いろんな方法で一直線上であることを示しにいくんだけど、これが結構難しい。例えばようこちゃんはどんな風に証明する?
え? そりゃ、状況次第だけど、例えば3点が\(A, B, C\)の順に並んでいるときに、線分\(AB\)と線分\(BC\)のなす角が\(180^{\circ}\)になること、とか。ベクトルを使って、\(\overrightarrow{AB} = k\overrightarrow{AC}\)となる定数\(k\)が存在することとか、かな。
うん。色々な条件があるけど、とにかく一直線上で成り立つ関係式を示せばよくて、問題に応じて柔軟に示せそうなゴールを”自分で”決めて、それに向かって突っ走るってことが大事だね。無理そうなら、ゴールを変えてもう一度考え直すってことになる。だから、問題としては難しくなりやすいよね。
まぁ、でも練習しておきたいな。
おっけい。じゃあ、この問題を。
1983年 第2問 つかみどころがない
\(\angle A = 90^{\circ}\)である直角三角形\(ABC\)がある。頂点\(B, C\)をそれぞれ始点として、辺\(BC\)に垂直な半直線\(l, m\)を頂点\(A\)のある側に引く。つぎに辺\(BC\)上の任意の点\(P\)より辺\(AB, AC\)に垂線をひき、この延長が\(l, m\)と交わる点をそれぞれ\(Q, R\)とする。
(1) 3点\(Q, A, R\)は一直線上にあることを示せ。
(2) 台形\(BCRQ\)の面積が三角形\(ABC\)の面積の\(2\)倍になるとき、この台形の形を求めよ。ただし、\(AB\neq AC\)とする。
この問題、辺の情報も辺の比の情報も全くないから、どうしても解きにくく見えるかも。
とにかく、平面図形は図が大事なはず。
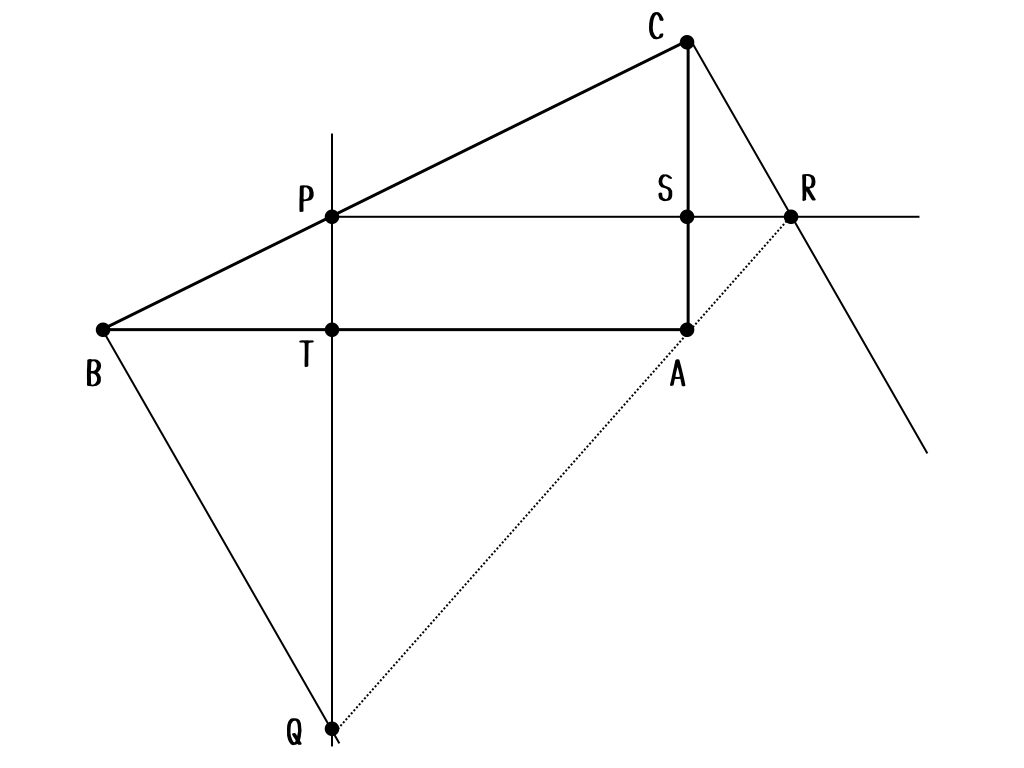
こう見ると、角度が\(90^{\circ}\)ってことだけしかわかっていないよね。
う〜ん。そうなんだよ。手をつけようにも、どうにもつかみどころがないって感じ。じゃあ、どうするか。
まぁ、自分でパラメータを設定していくしかないよね。また、私の趣味で設定していいかな?
どうぞどうぞ。やってみて。
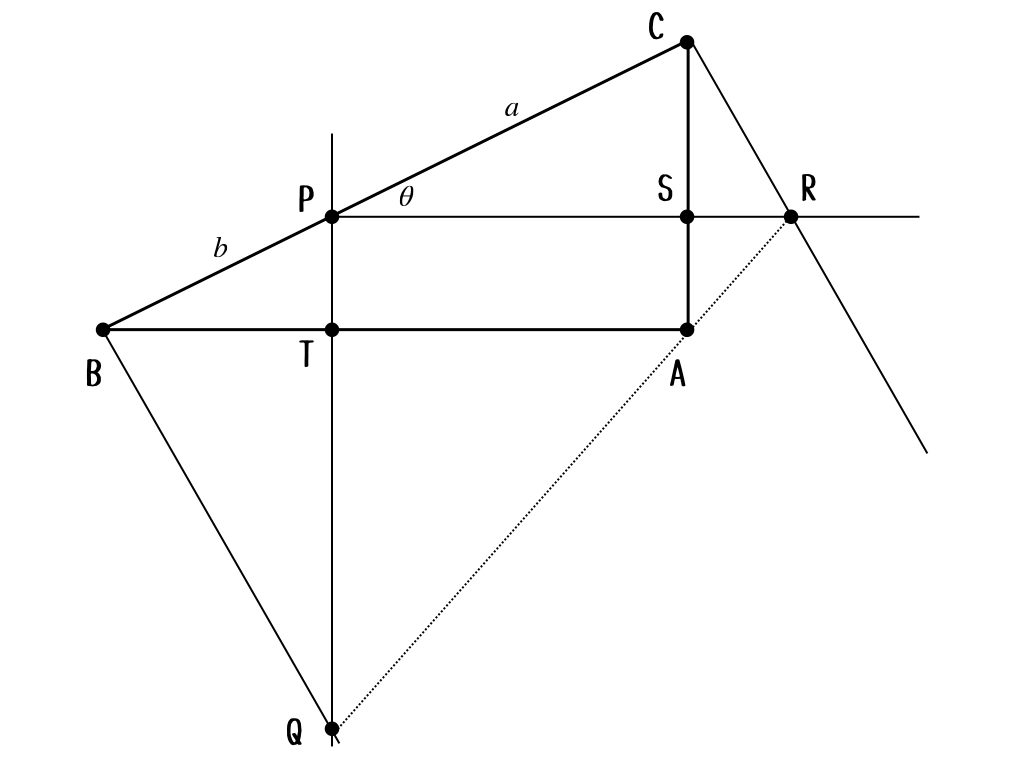
うん。いいと思うよ。この3つのパラメータはいいとっかかりになるかも。
じゃあ、色々な辺の長さや角度を求めていこっかな。
ストップ、ようこちゃん。まずはゴールを確認した方がよくない? \(R, A, Q\)が一直線上になるためには、何を証明すれば良さそう?
どうだろう。どうやって考えたらいいのかな。
そうだねぇ。ポイントは、まずは、一直線上だったら成り立つことを考えてみることだよ。
\(R, A, Q\)が一直線上にあったら、例えば\(△RSA\)と\(△RPQ\)が相似だね。他にも、同位角が等しいってことから\(\angle SAR = \angle PQR\)とかかな。
そうそう。で、その条件を見つけたら、逆が正しいかどうかも考えるんだ。例えば、\(△RSA\)と\(△RPQ\)が相似だったら\(R, A, Q\)が一直線上にあるかどうかってこととか、\(\angle SAR = \angle PQR\)が成り立っていたら、\(R, A, Q\)が一直線上にあるかどうかってこととか、を考えるんだ。これの逆が正しくないと証明する意味がないからね。
少なくとも同位角の方は逆も正しいと思うな。点\(R\)を共有しているんだから、一直線じゃないと同位角にならないから。
そうだね。逆が正しいかどうかの考え方としてはこんなのもあるよ。
1. 点\(R, A\)を結ぶ直線と辺\(PQ\)の交点を\(R^{\prime}\)とする。
2. このとき、平行線の同位角が等しいから、\(\angle SAR^{\prime} = \angle PQR^{\prime}\)
3. もし、\(\angle SAR = \angle PQR\)が成り立つなら、\(R, R^{\prime}\)は一致する。
4. だから、\(R, A, Q\)は一直線上にある。
なるほど。それなら、確かに一直線上の証明になる。
こういう考え方って、結構役に立つこともあるから、覚えておいてもいいかも。まぁ、とにかく、狙いは\(△RSA\)と\(△RPQ\)が相似だってことを示して、\(\angle SAR = \angle PQR\)を示す、だね。
なるほど、だから、相似に必要な辺の長さを中心に求めていくってわけだね。ゴールがわからないと、とにかく手当たり次第に辺の長さを求めることになっちゃうから、それを防ぐってことか。

まずは角度\(\theta\)になるところを調べてみたよ。直角三角形がいっぱいあるから、相似になるところが多くて結果的に\(\theta\)になるところも多いね。
うん。いい感じ。
次は、\(PR, RS\)の辺を求めてみるよ。この問題、\(R, A, Q\)が一直線上になることを前提としていないから、2つの角度で相似をいうのは多分無理で、相似を証明できるとすれば、二辺の比とその間の角度が等しい、っていう条件だと思うからね。
うん、いい感覚だね。
そうすると三角比を使って、こんな感じかな。
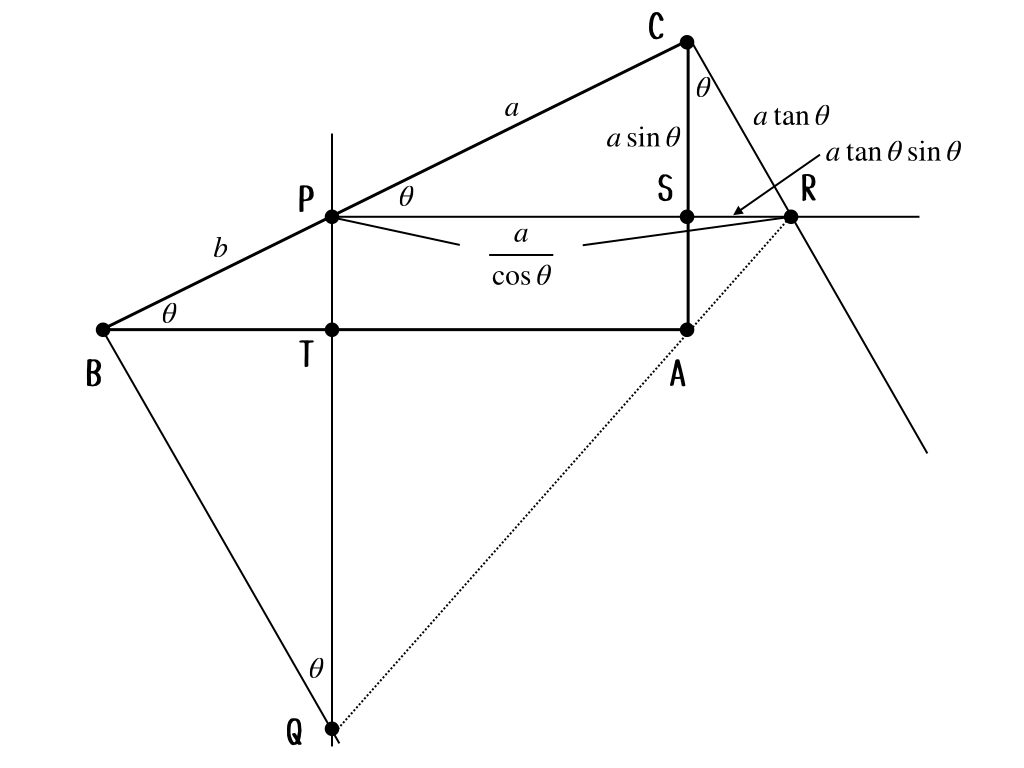
そうだね。ようこちゃんの図だと
$$SR = a\tan{\theta}\sin{\theta},\ PR = \frac{a}{\cos{\theta}}$$
かな。
うん。ちょっと形は汚いけど。まぁ、大丈夫でしょ。次は\(PQ, SA\)を求めるよ。
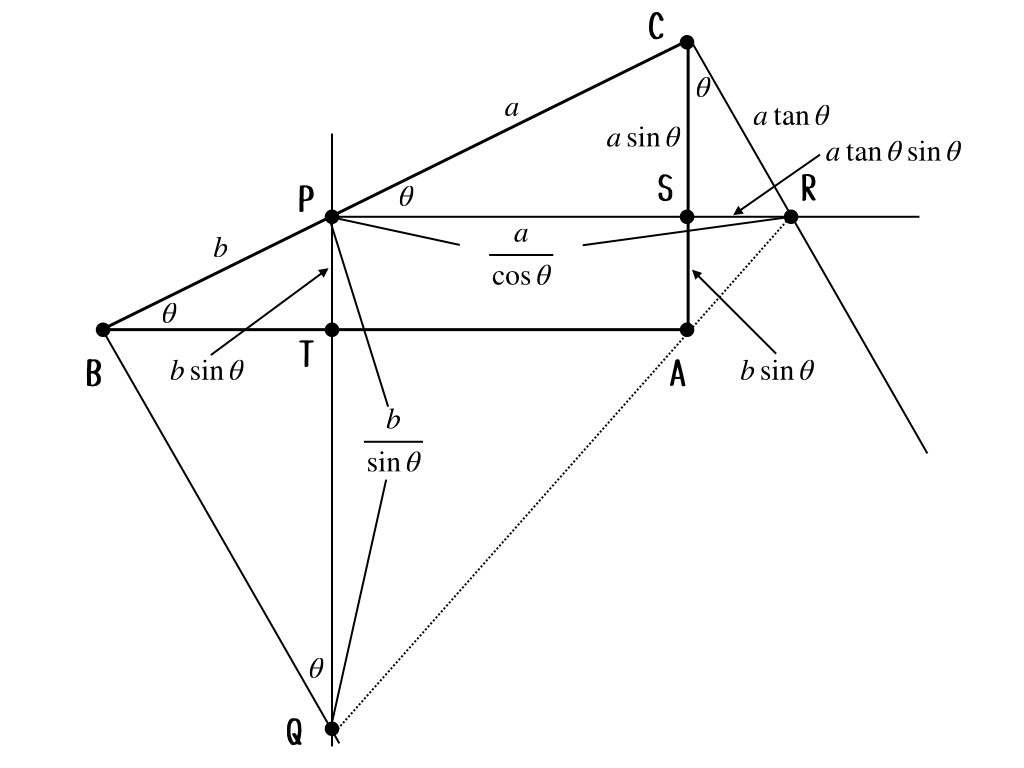
なんか、充実してきたじゃん。これで、必要なものは全て揃ったかな。
かな? あとは同じになりそうもないけど、二辺の比を比較してみるんだけど
$$SR : SA = a\tan{\theta}\sin{\theta} : b\sin{\theta}$$
$$SR : SA = a\frac{\sin^{2}{\theta}}{\cos{\theta}} : b\sin{\theta} = a\sin{\theta} : b\cos{\theta}$$
で、大きな三角形の方は
$$PR : PQ = \frac{a}{\cos{\theta}} : \frac{b}{\sin{\theta}} = a\sin{\theta} : b\cos{\theta}$$
で、一致した、、、。
予定調和、予定調和。だって、大学の入試問題だもん。
そんなに簡単に割り切れないけど、とにかく二辺の辺の比とその間の角が等しいから相似で、相似な三角形の関係から\(\angle SAR = \angle PQR\)だね。で、さっきの議論から、このとき\(R, A, Q\)が一直線上にあることが証明できたね。
うん。おっけい。ちなみに、一直線上の証明では、この図形を座標平面上において考えるとよりわかりやすいかもね。今の場合だったら、直線\(RA\)と直線\(RQ\)または直線\(QA\)の傾きが等しいことを言えば、一直線上になるから。
確かに、それでも良さそう。ただ、この問題は(2)があるから、幾何として解きたかったかな。
方法は色々あるからね。この方法もそんな無理な方法じゃなかったと思うし。じゃあ、(2)を解いてみよう。
台形の形を求めよ、って初めて見たけど。
等脚台形になるとか、または長方形になるとか、正方形になるとか、そんな感じかな。さぁ、どうしよう。
私の方法だと、ちょっと面倒くさいけど、台形\(BCRQ\)の面積と三角形\(ABC\)の面積を直接求めて、何らかの関係式を導くって方法になっちゃうんだけど、どうだろう?
うん。それが一番確実ではあるよね。あとは、計算力勝負。
まぁ、今回のテーマの1つは”計算能力”を高めることだし、思い切ってそれでやってみるよ。間違ったら、教えてね。
は〜い。頑張って。
まず、必要な辺の長さを加えておこう。図がごちゃごちゃしちゃうから、いらない辺の長さは消しちゃうね。
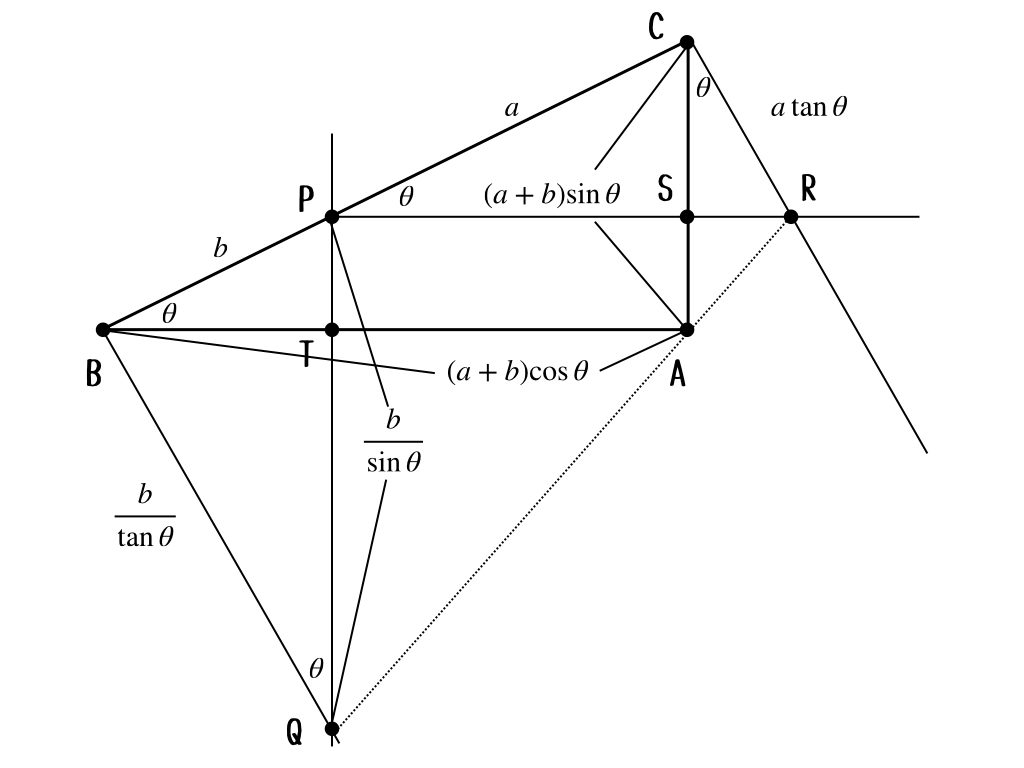
さて、この図で台形\(BCRQ\)の面積\(S_{1}\)は
$$S_{1} = \frac{1}{2}\left( a\tan{\theta} + \frac{b}{\tan{\theta}} \right)(a+b)$$
で、三角形\(ABC\)の面積\(S_{2}\)は
$$S_{2} = \frac{1}{2}(a+b)^{2}\cos{\theta}\sin{\theta}$$
だね。台形の方が2倍の面積なんだから
$$a\tan{\theta}+\frac{b}{\tan{\theta}} = 2(a+b)\sin{\theta}\cos{\theta}$$
が成り立つ。ん〜、とりあえずタンジェントをサインとコサインで表すと
$$a\frac{\sin{\theta}}{\cos{\theta}}+b\frac{\cos{\theta}}{\sin{\theta}} = 2(a+b)\sin{\theta}\cos{\theta}$$
$$a\sin^{2}{\theta} + b\cos^{2}{\theta} = 2(a+b)\sin^{2}{\theta}\cos^{2}{\theta}$$
とにかく無理やり\(=0\)の形まで持っていくと
$$a\sin^{2}{\theta}(1-2\cos^{2}{\theta})+b\cos^{2}{\theta}(1-2\sin^{2}{\theta}) = 0$$
だね。
うん、そこまではいいよ。
もっと簡単にしたいなぁ。倍角の公式を使うと
$$-a\sin^{2}{\theta}\cos{2\theta} + b\cos^{2}{\theta}\cos{2\theta} = 0$$
$$\cos{2\theta}(b\cos^{2}{\theta}-a\sin^{2}{\theta}) = 0$$
ようやく、形になってきた!
この方程式の解は
$$\cos{2\theta} = 0,\ b\cos^{2}{\theta} = a\sin^{2}{\theta}$$
ふむふむ。ここで、さりげなく条件が適用できそうだね。
え〜と、あ、そうか。\(\cos{2\theta} = 0\)ってことは、今の場合\(\theta < 90^{\circ}\)なんだから\(\theta = 45^{\circ}\)ってことだね。で、この場合は\(AB=AC\)になっちゃうから不適切ってことか。そうすると、もう1つの条件、より簡単にすると
$$\tan^{2}{\theta} = \frac{b}{a}$$
が満たされなきゃいけない。\(\tan{\theta}\)が負になることはないから
$$\tan{\theta} = \sqrt{\frac{b}{a}}$$
で、台形はどんな形だ?
それを調べるためには、台形の辺の長さを調べるのがいいかな。
そうだね。
\(RC = a\tan{\theta} = \sqrt{ab},\ BQ = \frac{b}{\tan{\theta}} = \sqrt{ab}, BC = a+b\)
で、長方形、かな?
まだ、結論するには早いよ!
あっ、そうか。辺の長さを比べないとね。え〜と、相加・相乗平均かな。
$$a+b \geq 2\sqrt{ab} > \sqrt{ab}$$
だから、うん、正方形にならない。この台形の形は長方形になる!
パーフェクト! 計算お疲れ様。
このやり方だから大変になったんだろうな。もっとエレガントに解ける解法があると思う。
まぁ、でも入試の本番では、エレガントに解ける解法より、25分~30分で思いついて確実に解ききれる解法であれば、なんでもいいからね。ようこちゃんの選んだ解き方は、複雑すぎることもないし、十分試験内で対応できる方法だと思うよ。
そっか。私の場合は、確実に解けそうな解法に食らいついちゃうからなぁ。
あたしもそうだよ。たま〜に、簡単に解ける方法も思いつくけど。だから、計算能力が大事なんだよね。
ふ〜。今日は、こんなところかな。
あれ? ようこちゃん、もう終わり? まだ、平面図形の重要な問題をやっていないよ。
え? そうなの。もう十分やった気がするんだけど。
まぁ、だいたいね。でも、まだ、”定点問題”をやってないよ。
定点問題? え〜と、どんなのだっけ。
ある条件に従う直線が、その条件を満たす限りにおいて常に”定点”を通ることを証明する問題だよ。やっておかないと、どうやって証明するかもわからない問題で、難問になりやすいよ。
そうかぁ。じゃあ、あとちょっと頑張るか。
1979年 第5問 六芒星の秘密
中心が\(O\)である定円の周上に相異なる6つの定点\(A_{1}, A_{2}, A_{3}, A_{4}, A_{5}, A_{6}\)がある。このとき
(ⅰ) \(\overrightarrow{OA_{1}} + \overrightarrow{OA_{2}} + \overrightarrow{OA_{3}} = \overrightarrow{OH}\)となるように点\(H\)を取れば、点\(H\)は\(△A_{1}A_{2}A_{3}\)の垂心であることを示せ。
(ⅱ) 6点\(A_{k} (k=1, 2, 3, 4, 5, 6)\)のうちから3点にえらぶ。えらんだ3点を頂点とする三角形の垂心と、残りの3点を頂点とする三角形の重心とを通る直線は、3点のえらびかたに無関係な一定の点を通ることを示せ。
注 三角形の各頂点からその対辺にひいた3つの垂線は1点で交わる。この交点をその三角形の垂心という。
ちなみに、文系の問題では、(ⅰ)がなくて”垂心”が”重心”になっているね。重心だと難易度が下がるし、文理の入試問題として最高の使い分けだと思うよ。
ベクトルかぁ。(ⅰ)はすぐに解けそうなんだけど、(ⅱ)はちょっと見当もつかないなぁ。
ようこちゃん、なにはともあれ、でしょ。
そうだね。なにはともあれ、図を描いてみようか。
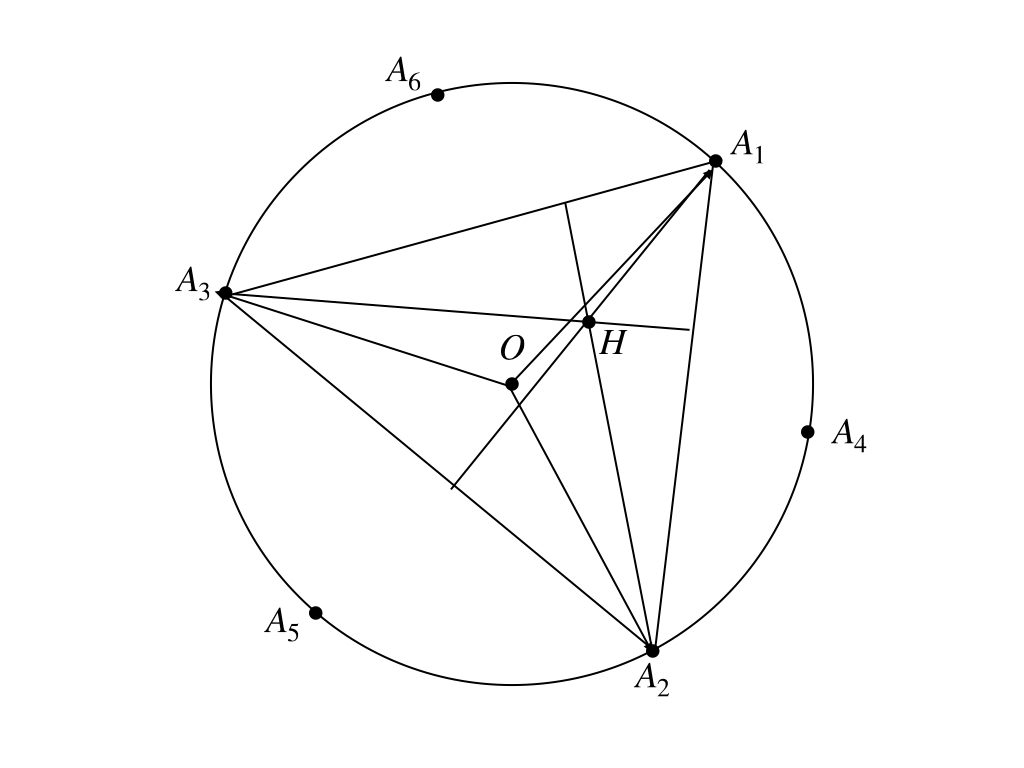
え〜と、(ⅰ)はようこちゃんにとっては楽勝?
多分、、、。やり方はわかる気がする。つまり、\(\overrightarrow{A_{1}H}\)が\(\overrightarrow{A_{3}A_{2}}\)と、\(\overrightarrow{A_{2}H}\)が\(\overrightarrow{A_{1}A_{3}}\)と垂直だってことを言えばいいね。やってみるよ。垂直をいうには、2つのベクトルの内積が0だってことを言えばよくて。
$$\overrightarrow{A_{1}H}\cdot\overrightarrow{A_{3}A_{2}}=(\overrightarrow{OA_{2}}+\overrightarrow{OA_{3}})\cdot(\overrightarrow{OA_{2}}-\overrightarrow{OA_{3}})$$
$$ = |\overrightarrow{OA_{2}}|^{2} – |\overrightarrow{OA_{3}}|^{3} = 0$$
半径が等しいからね。\(\overrightarrow{A_{2}H}\)と\(\overrightarrow{A_{1}A_{3}}\)の内積も同じように計算できるから、点\(H\)は\(△A_{1}A_{2}A_{3}\)の垂心で間違いないね。
うん、そんな感じだね。さて、問題の(ⅱ)だ。どう攻めるかが難しいところ。
ま、とにかく図を描くよ。
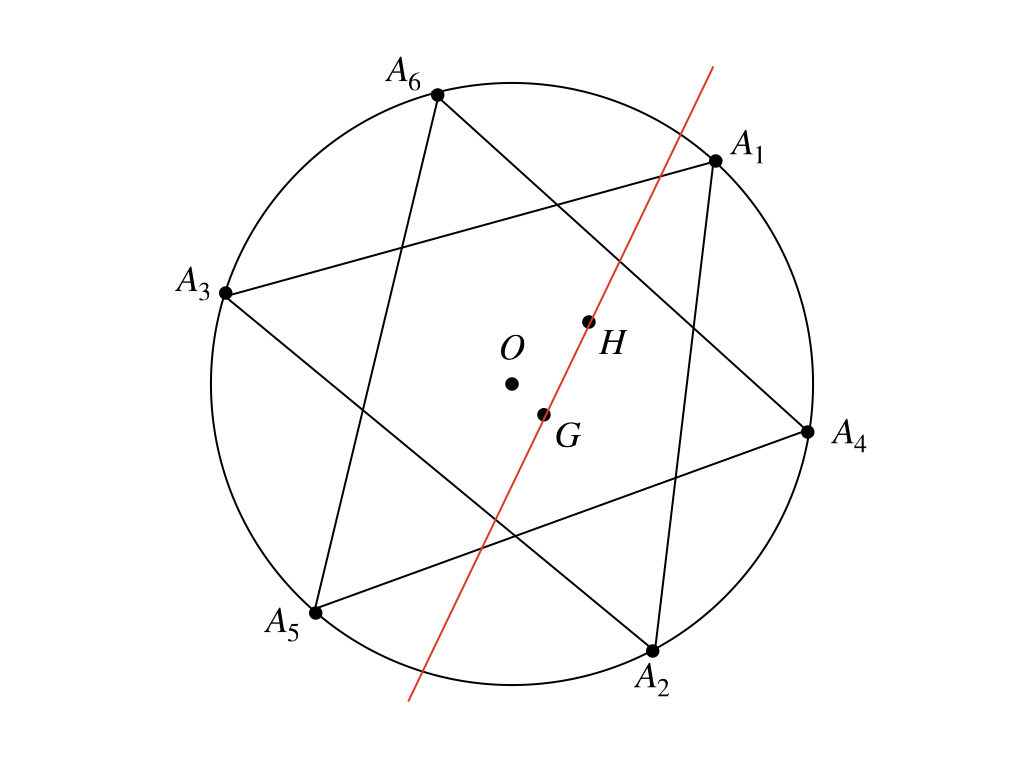
なんか、魔法陣みたいだね。
うん、、、。六芒星っぽくなっちゃった。それに、あんまり、図は参考にならない気がするなぁ。
定点の見当がつけばいいけど、どう?
真っ先に思いつくのは、中心\(O\)とかだけど、この図ですらまともに通っていないから、違うっぽい。3点が作る三角形の重心と別の3点が作る三角形の重心だったら、必ず6角形の重心を通るんだけどね。
うん。定点の問題って、予想がつけばそれを証明しにいけばいいんだけど、大抵の場合、どこが定点になるかわからないよ。だから、文系の問題は比較的易しいってことなんだけど、この問題は、じゃあどうするってことだよね。まず、なにを使って証明するか決める?
まぁ、ベクトルを使いたいかなぁ。一応(ⅰ)を信頼するならね。ってことで、一応重心\(G\)のベクトルも求めると
$$\overrightarrow{OG} = \frac{\overrightarrow{OA_{4}} + \overrightarrow{OA_{5}} + \overrightarrow{OA_{6}}}{3}$$
だけど、だからどうなのって感じ。
良〜し、じゃあヒント。定点候補を点\(X\)とおいてみようか。それで、\(\overrightarrow{OX}\)を求められる? 文字を使ってもいいよ。
う〜ん。それならできるかな。つまり、
$$\overrightarrow{OX} = \overrightarrow{OH} + k\overrightarrow{HG}$$
ってことだよね。
その通り。じゃあ、計算してみる?
$$\overrightarrow{OX} = (\overrightarrow{OA_{1}} + \overrightarrow{OA_{2}} + \overrightarrow{OA_{3}} + k\left( \frac{\overrightarrow{OA_{4}} + \overrightarrow{OA_{6}} + \overrightarrow{OA_{6}}}{3} – (\overrightarrow{OA_{1}} + \overrightarrow{OA_{2}} + \overrightarrow{OA_{3}}) \right)$$
$$\overrightarrow{OX} = (1-k)(\overrightarrow{OA_{1}} + \overrightarrow{OA_{2}} + \overrightarrow{OA_{3}}) + \frac{k}{3}(\overrightarrow{OA_{4}} + \overrightarrow{OA_{6}} + \overrightarrow{OA_{6}})$$
という感じ。まだ、掴みきれていないなぁ。
ここが頭の使い所だよ。ようこちゃんなら思いつくって! 定点をどう扱うかってことだよ。
定点は定点だよね。条件を満たすどんな直線でもその点を通るってことでしょ。ん? だから、定点は必ず、交点にもなっている。交点、交点か。交点は、ベクトルの十八番じゃん。ってことは、この\(X\)を別の条件で試せばいいってことかな。
ズバリ、その通り。ただ、現時点ではまだ定点が存在することはわかっていない(それを証明しようとしている)から、\(X\)と置くのは危険だね。
そうだね。じゃあ、\(Y\)とおいておくよ。つまり、垂心と重心を考える三角形を変えればいいってことだから、いっそ、垂心と重心となる三角形を逆転させてしまおう。つまり、\(△A_{1}A_{2}A_{3}\)の重心を\(G^{\prime}\)、\(△A_{4}A_{5}A_{6}\)の垂心を\(H^{\prime}\)とする。すると、さっきの結果を使って、文字は\(m\)とすると
$$\overrightarrow{OY} = (1-m)(\overrightarrow{OA_{4}} + \overrightarrow{OA_{5}} + \overrightarrow{OA_{6}}) + \frac{m}{3}(\overrightarrow{OA_{1}} + \overrightarrow{OA_{2}} + \overrightarrow{OA_{3}})$$
ってことだ! で、で、\(X\)と\(Y\)が一致するような\(k, m\)があればいいわけだね。それが両方とも同じベクトルで表せれば、定点候補になる。\(OA_{i} (i=1, 2, 3, 4, 5, 6)\)はどの2つも一次独立だから係数比較ができて、
$$1-k = \frac{k}{3}, \frac{k}{3} = 1-m$$
となるから、これを解くと\( k = m = \frac{3}{4}\)になる。え? そうすると、
$$\overrightarrow{OX} = \overrightarrow{OY} = \frac{\overrightarrow{OA_{1}} + \overrightarrow{OA_{2}} + \overrightarrow{OA_{3}}+\overrightarrow{OA_{4}} + \overrightarrow{OA_{5}} + \overrightarrow{OA_{6}}}{4}$$
だから、これが定点じゃん!
そう、それが”定点候補”だよね。それを発見したようこちゃんはすごいけど、まだ、それは定点になってない。だって、2つの直線の交点を見つけただけだからね。じゃあ、それが定点であることをどうやって示す?
あっそうか。まみは鋭い。てっきりこれで終わりかと思っちゃった。確かに一般性は欠いていたね。じゃあ、ベクトルを\(\overrightarrow{OA_{a}}, \overrightarrow{OA_{b}}, \overrightarrow{OA_{c}}, \overrightarrow{OA_{d}}, \overrightarrow{OA_{e}}, \overrightarrow{OA_{f}}\)とおいて、それぞれ\(a, b, c, d, e, f\)は順不同で\(1, 2, 3, 4, 5, 6\)に対応するとするよ。それで、\(\overrightarrow{OA_{a}}, \overrightarrow{OA_{b}}, \overrightarrow{OA_{c}}\)で垂心をとり、他ので重心をとるとする。そうすると直線\(HG\)上の点\(X\)は、
$$\overrightarrow{OX} = (1-k)(\overrightarrow{OA_{a}} + \overrightarrow{OA_{b}} + \overrightarrow{OA_{c}}) + \frac{k}{3}(\overrightarrow{OA_{d}} + \overrightarrow{OA_{e}} + \overrightarrow{OA_{f}})$$
だけど、ここで\(k=\frac{3}{4}\)とすれば、
$$\overrightarrow{OX} = \frac{\overrightarrow{OA_{a}} + \overrightarrow{OA_{b}} + \overrightarrow{OA_{c}}+\overrightarrow{OA_{d}} + \overrightarrow{OA_{e}} + \overrightarrow{OA_{f}}}{4}$$
となって、\(a, b, c, d, e, f\)がどういう風に割り当てられても、必ず同じ点になる。だから、この\(X\)は定点だね。
パーフェクトだよ。\(k=\frac{3}{4}\)を発見するために、2直線で交点を作ったんだね。勘のいい人はすぐにこれを予想できたかも。予想できちゃうと、時間と回答スペースを大幅に削減できるから。
もし重心と重心を結ぶ直線上の定点を探す問題だったら、六角形の重心が定点になることが予想できて、
$$\overrightarrow{OX} = \frac{k}{3}(\overrightarrow{OA_{a}} + \overrightarrow{OA_{b}} + \overrightarrow{OA_{c}}) + \frac{k}{3}(\overrightarrow{OA_{d}} + \overrightarrow{OA_{e}} + \overrightarrow{OA_{f}})$$
から
$$\overrightarrow{OX} = \frac{\overrightarrow{OA_{a}} + \overrightarrow{OA_{b}} + \overrightarrow{OA_{c}}+\overrightarrow{OA_{d}} + \overrightarrow{OA_{e}} + \overrightarrow{OA_{f}}}{6}$$
を作ればいいって予想できるから、\(k=\frac{1}{2}\)とすればいいことが見えるから、比較的簡単だってことなんだね。
そうそう。これで、ついでに文系の問題も解いちゃったね。
なるほどね〜。
今、ようこちゃんが解いたように、定点問題では定点が予想できればそんなに難しくないんだ。じゃあ、どうやって定点を予想するかっていうと、例えば図をきれいに描くとか、あとは2通りの条件で直線を2つ作って、その交点がどんな点になっているかを考えると上手くいくよ!
1. 定点となる点を予想できる場合
→ それが定点となることを示す。
2. 定点となる点が予想できない場合
→ 2つの条件で2つの直線を作って、その交点を求める。
→ その交点がどんな点となるのかを考える。
→ その交点が定点となることを示す。
漠然としているけど、こんな感じかな。
うまい感じにまとまってると思うよ。
これが定点問題か、じゃあ、もう1問。
いいね〜、じゃあ、これだ!
1962年 第3問 よく見つけたな、こんな点
定円\(O\)の内部に2定点\(A, B\)があり、点\(P\)はこの円周上を動いていく。\(P\)と\(A\), \(P\)と\(B\)を結ぶ2直線が円周とふたたび交わる点を、それぞれ\(Q, R\)とする。また、\(Q\)から直線\(AB\)に平行に引いた直線が円周とふたたび交わる点を\(S\)とする。このとき、直線\(RS\)は1つの定点を通ることを証明せよ。
なんか複雑なことをしているように見える。けど、どうなんだろう。
文字を追っていると何をやっているのかよくわかんないよね。
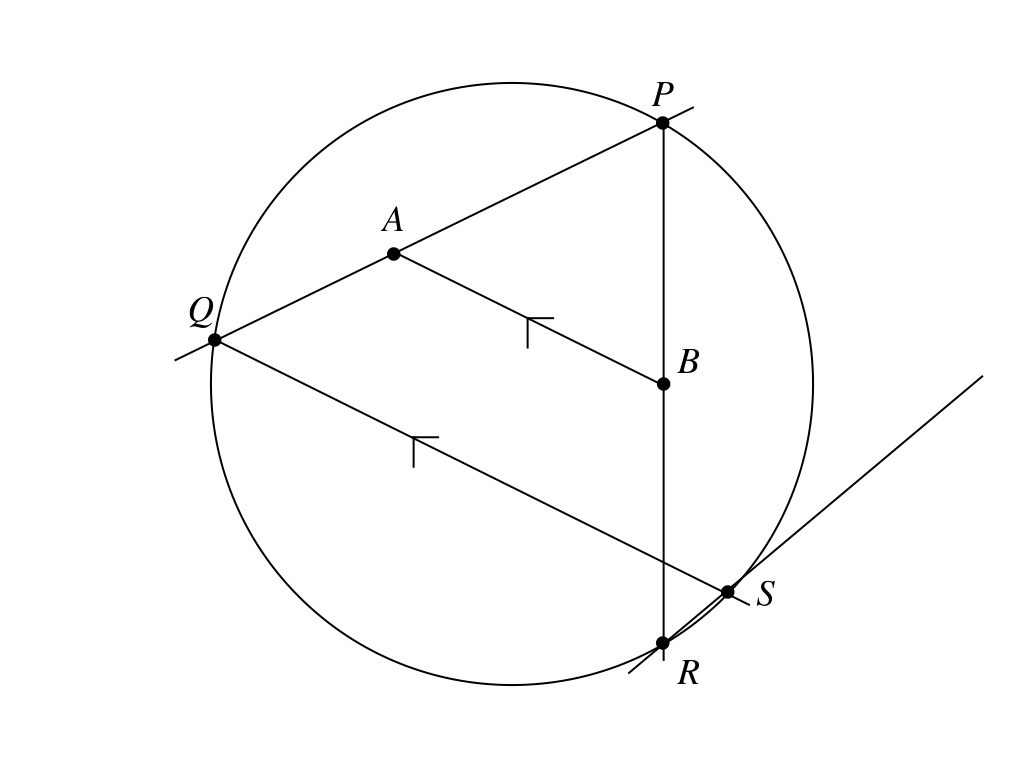
こういうことだね。
この問題、はっきり言って、難問だと思う。でも今日、解いてきた問題の集大成としてはふさわしいよ。ようこちゃん、頑張って解いてみてよ。
頑張って、と言われてもなぁ。まぁ、じゃあ、頑張ってみるか。定点問題で、どこが定点になるかわからないから、違う条件で作図してみるよ。
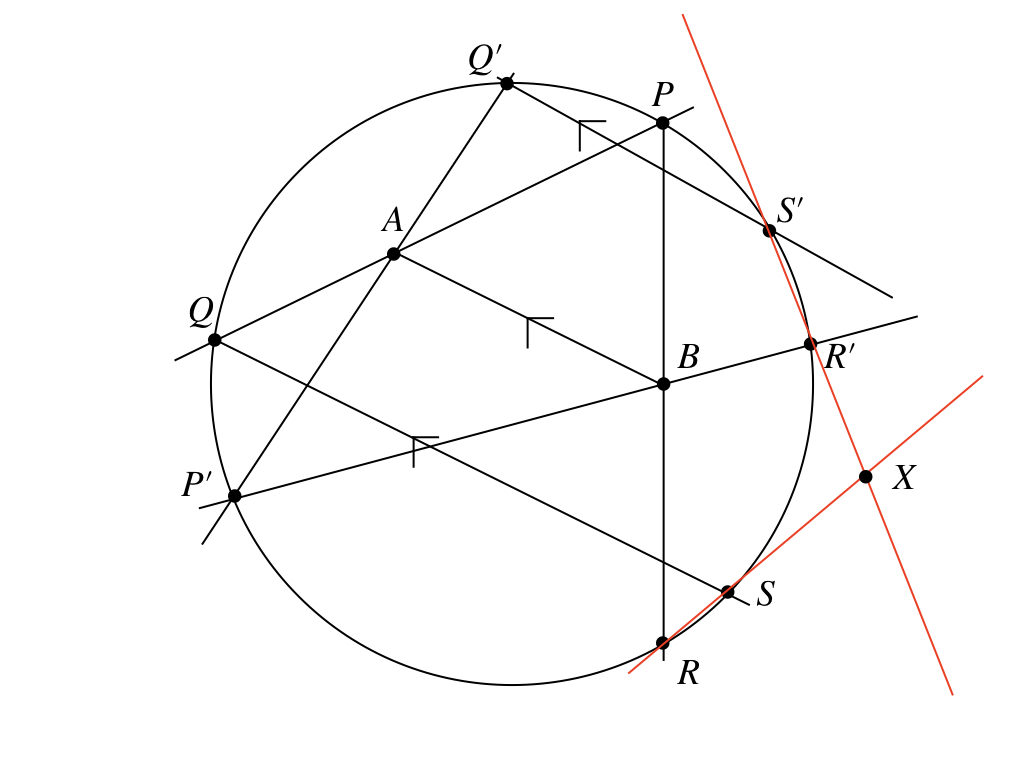
この図で、\(X\)が2直線の交点だね。う〜ん、なんとなく、だけど、定点\(A, B\)と関係ありそうなことでは、直線\(AB\)上にある気はするけど、なんとも言えないなぁ。もう一度引きなおしてみようかな。
うんうん。
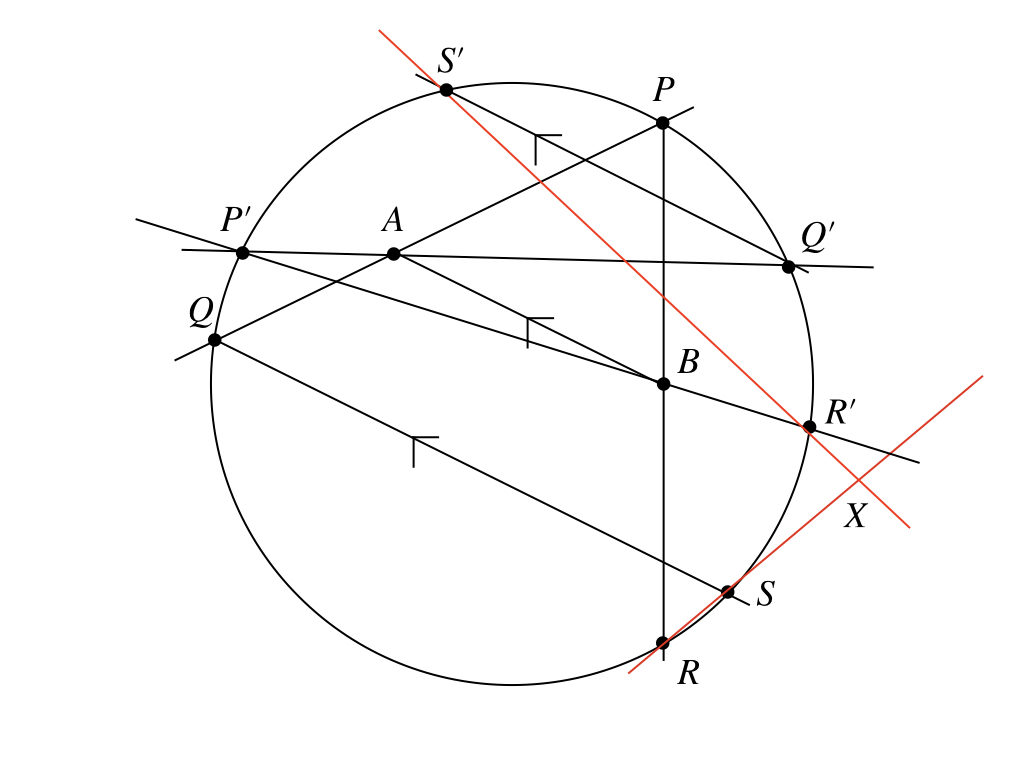
うん、これはやっぱり、直線\(AB\)上にあるよ。でも、直線\(AB\)上にあるってだけじゃ、\(X\)が定点になるとは限らないか。なんか\(BX\)の長さが一意に決まってることもわかれば完璧なんだけどなぁ。
ふむふむ。
つまり
1. 点\(X\)が直線\(AB\)上にある
2. \(BX\)の長さがいつも等しい
という2つのことが証明できれば、\(X\)は定点になる。
ほうほう。
……。教えてくれる気、ないでしょ。ん〜、じゃあ、とりあえず、こういうことをするのかな?
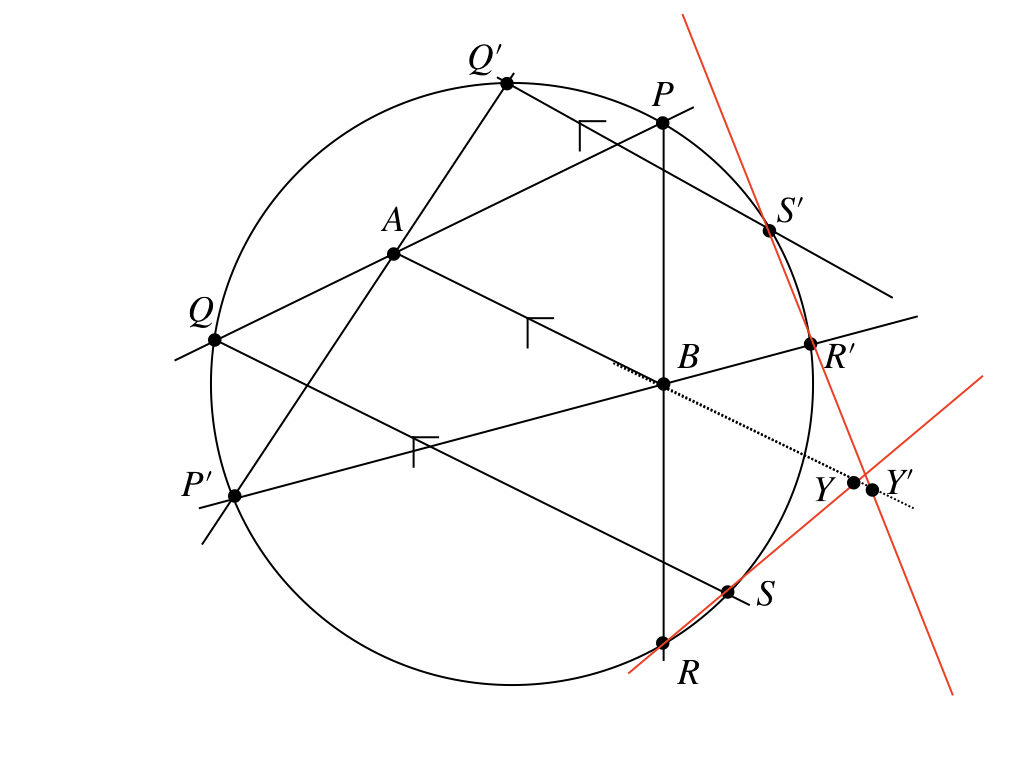
点\(Y\)は直線\(AB\)と直線\(RS\)の交点。点\(Y^{\prime}\)は直線\(AB\)と直線\(R^{\prime}S^{\prime}\)の交点。これで、1の条件はクリア。だから、あとは\(BY = BY^{\prime}\)を示せば、\(Y, Y^{\prime}\)は一致して、これが定点となる、はず。なんか、見えてきた。
惚れ惚れするね、ようこちゃん。
ってことは、方針は大丈夫ってことかな。とりあえず、\(A, B, Y\)が一直線上にあることは使っていいんだから、これで何が言えるか、考えようかな。
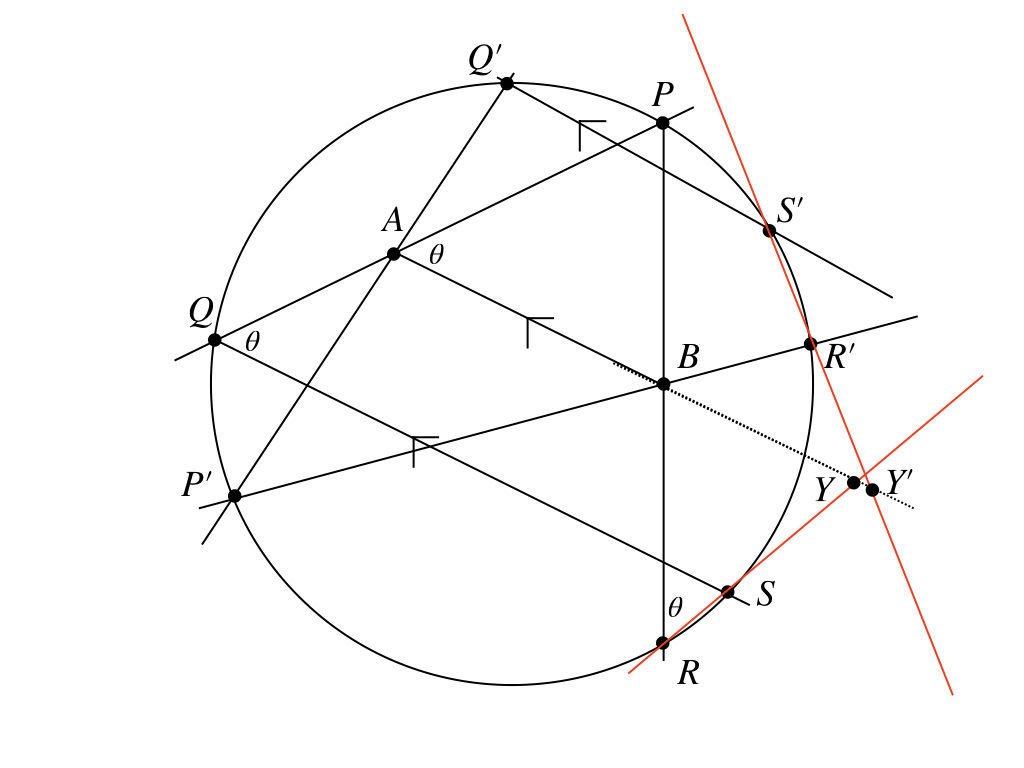
とりあえず、等しい辺はこんな感じかな。円周角の定理から\(\angle YRB = \angle PQS\)で、平行線の同位角だから\(\angle PQS = \angle PAB\)だね。あ〜、てことは相似か。
$$△YBR \sim △PBA$$
ん? ってことは、もう1つの方も同じような関係があるかな。
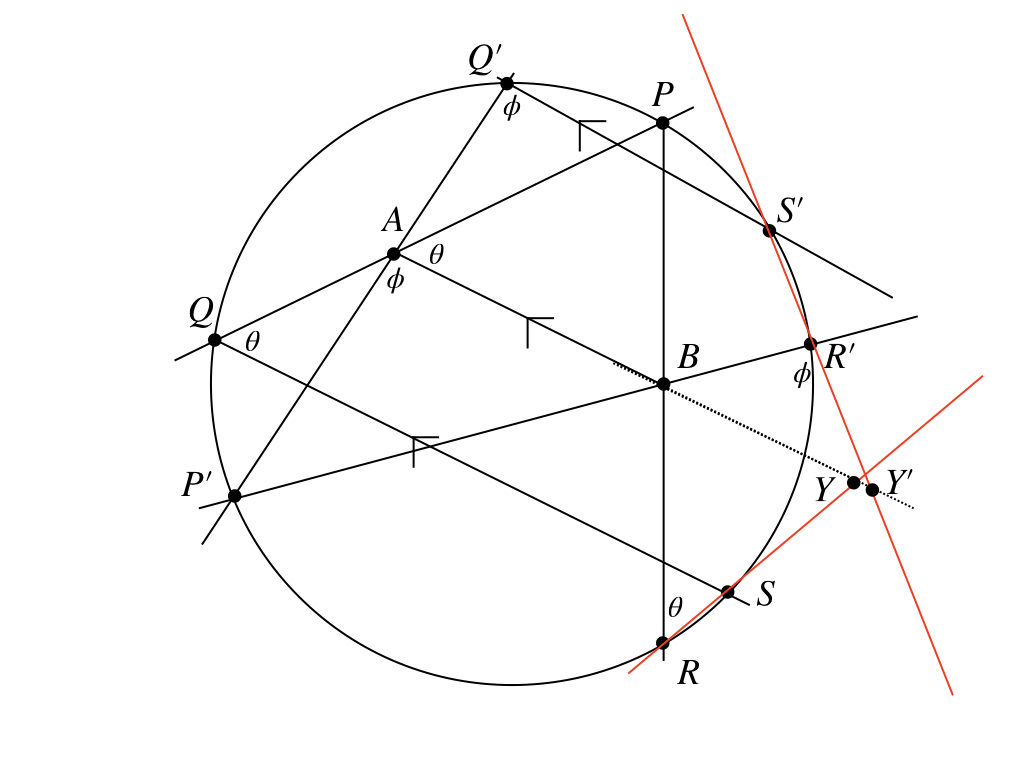
同じ角度をマークすると、こうなる。今度は、\(P^{\prime}Q^{\prime}S^{\prime}R^{\prime}\)が円に内接する四角形であるという性質を使って、\(\angle P^{\prime}R^{\prime}Y^{\prime} = \angle P^{\prime}Q^{\prime}S^{\prime}\)で、また平行線の同位角が等しいんだから
\( \angle P^{\prime}Q^{\prime}S^{\prime} = \angle P^{\prime}AB\)となる。だから、やっぱり相似だね〜。
$$△AP^{\prime}B \sim △R^{\prime}Y^{\prime}B$$
ちょっと、これ、いい感じじゃない?
……。
だんまり。ってことは、大丈夫、なのかな。まぁ、でもいい感じするし、続けよう。今わかったのは
$$△YBR \sim △PBA,\ △AP^{\prime}B \sim △R^{\prime}Y^{\prime}B$$
で、証明したいことは
$$BY = BY^{\prime}$$
だから、対応する辺の比を考えるとまず、上から
\(BY : BP = BR : BA\)で\(BY = \frac{BR\cdot BP }{BA}\)だね。下は、
\(BY^{\prime} : BP^{\prime} = BR^{\prime} : BA\)で\(BY^{\prime} = \frac{BR^{\prime}\cdot BP^{\prime}}{BA}\)となる。
ということは証明したいことは
$$BR\cdot BP = BR^{\prime}\cdot BP^{\prime}$$
なんだけど、、、。
ん〜? ん! あ、これ、あれじゃん!
ひらめいた? この瞬間て、何度味わっても気持ちいいよね。
わかった! 方べきの定理だね!
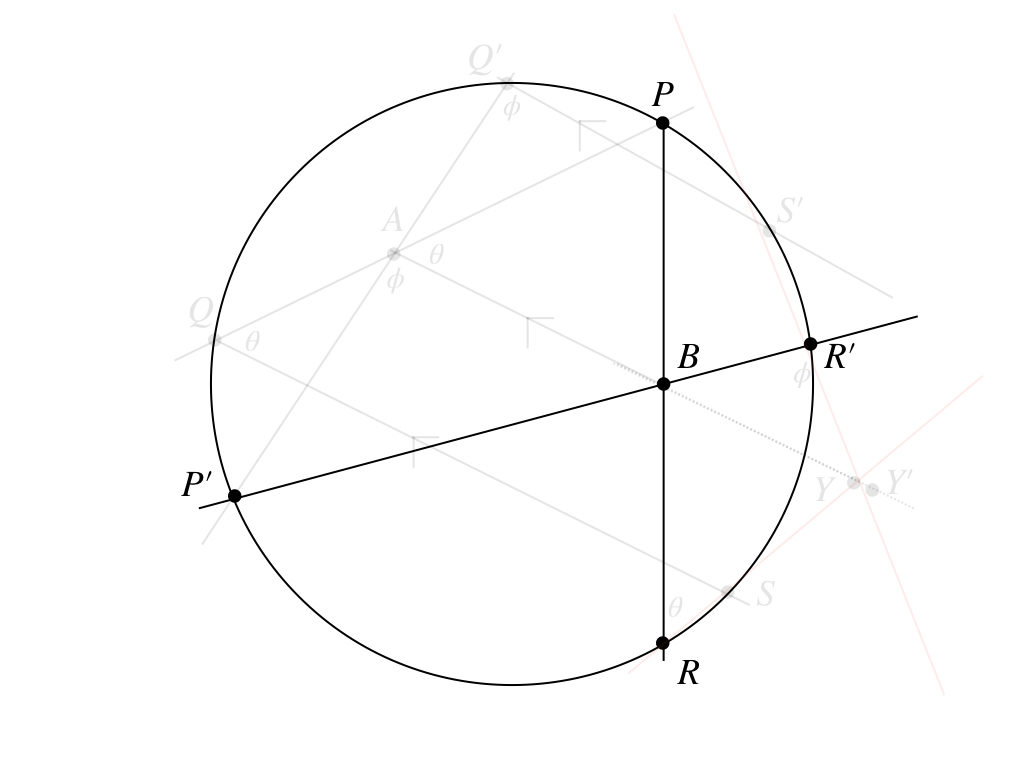
これだよ。これなら
$$BR\cdot BP = BR^{\prime}\cdot BP^{\prime}$$
が成り立つじゃん。これで、\(BY = BY^{\prime}\)になるよね。で、\(A, B, Y, Y^{\prime}\)は一直線上にあるんだから、\(Y, Y^{\prime}\)は一致。今の\(P, P^{\prime}\)の選び方は一般性を失わない。だから、この一致した点が定点となる。どうだ!?
お見事、お見事。
でも、1つ気になるなぁ。本当に、\(P, P^{\prime}\)の選び方は一般性を失わないかな? ようこちゃんの証明では、それぞれの選び方の時で、相似であることの証明が微妙に違ったよね。他の場合も同様に証明できることを、確認したかな?
……いや、してないけど。
結論から言うと、ようこちゃんのやり方でいいんだよ。なぜかって言うと、\(P\)の選び方には大きく分けて2種類しかなくて、それがちょうどようこちゃんの\(P, P^{\prime}\)の選び方と一致しているからなんだ。1つ目の選び方は、\(Q, R\)が直線\(AB\)に対して、同じ側の円周上にある場合。もう1つは\(Q, R\)が直線\(AB\)に対して異なる円周上の異なる位置にある場合。ようこちゃんの場合、偶然、\(P\)の選び方が前者で\(P^{\prime}\)の選び方が後者になってる。だから、他のどの点をとってきても\(P\)または\(P^{\prime}\)と同様の証明ができるんだよ。同様にできるってことは”一般性を失っていない”ってことだよね。
う〜んと、つまりOK?
う〜ん。厳密に言うと、\(P\)の選び方が2通りしかないことに触れておくべきかな。それで、他のどの点をとってきても\(P\)または\(P^{\prime}\)と同様の証明ができるってことを言うべきだと思う。でも、本質的には、ようこちゃんの証明で大丈夫だよ。ようこちゃんは無意識にやってたと思うけど、今の証明のストーリー、とてもよかったよ。
そ、そうなのかな。
そうだよ。重要なところを抜き出すとこんな感じ。
1. 定点の存在を予想
2. “定点が存在すること”と”点\(X\)が直線\(AB\)上にあって、\(BX\)の長さがいつも等しい”ことが同値であることを見抜く。
3. 具体的に\(Y, Y^{\prime}\)を\(A, B, Y, Y^{\prime}\)が一直線上にあるように取り、”点\(X\)が直線\(AB\)上にあって、\(BX\)の長さがいつも等しい”と”\(BY = BY^{\prime}\)”が同値であることを説明する。
4. 条件と”点\(Y, Y^{\prime}\)が直線\(AB\)上にある”ことと\(△YBR \sim △PAB,\ △AP^{\prime}B \sim △R^{\prime}Y^{\prime}B\)が同値であることを見出す。
5. \(△YBR \sim △PAB,\ △AP^{\prime}B \sim △R^{\prime}Y^{\prime}B\)から””\(BY = BY^{\prime}\)”と”\(BR\cdot BP = BR^{\prime}\cdot BP^{\prime}\)”が同値であることを示す。
6. 条件から方べきの定理を見つけて、\(BR\cdot BP = BR^{\prime}\cdot BP^{\prime}\)を示す。
7. 6から5, 3, 2と遡って定点が存在することを示した。
図で表すとこんな感じ?
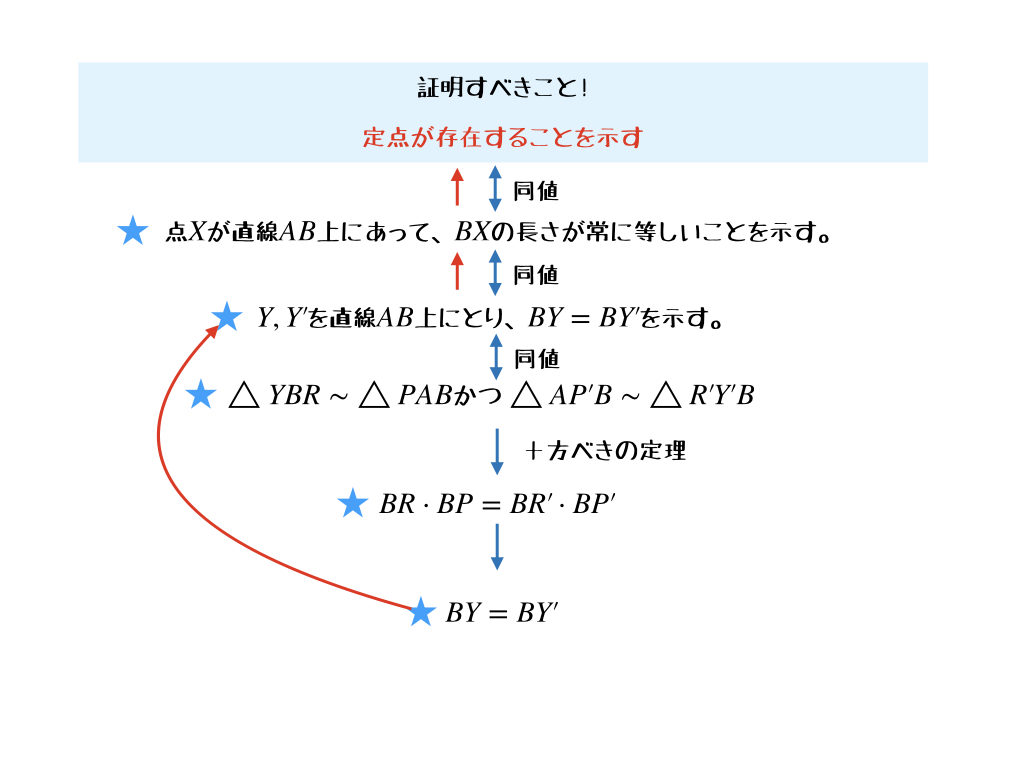
うわっ。こう見ると、すごいことやっちゃったんだね、私。
論理としては、少しだけ惜しかったけど、十分すごいと思う。
まぁ、そうだとしたら、まみのおかげだと思うよ。
でた、誉め殺し。ようこちゃんの実力だよ。
いやいや、そんなことないって。
まぁ、それはそうと、平面図形、面白かったでしょ?
そうだねぇ。ベクトルばっか使ってたけど、初等幾何もロマンがあるなぁ。
でしょでしょ。実は、空間図形も同じで、、、。
まさか、空間図形もやり始めるんじゃ、、、。
まさか! 次回やろうよ、次回。
次回、ね。苦手なんだよなぁ、空間。ま、でもよろしく!
おっけい!



コメント