数学オリンピック日本本戦2003年第1問の問題を解きます。
問題
三角形ABCの内部に点Pをとり、直線BPと辺ACの交点をQ, 直線CPと辺ABの交点をRとする。AR=RB=CPかつCQ=PQであるとき、∠BRCの大きさを求めよ。ただし、2点X, Yに対し、線分XYの長さをXYで表している。
感想
メネラウスの定理で一つのスッキリ、補助線で二つ目のスッキリを味わえます。よく思いつくなぁ、こういう問題。
回答
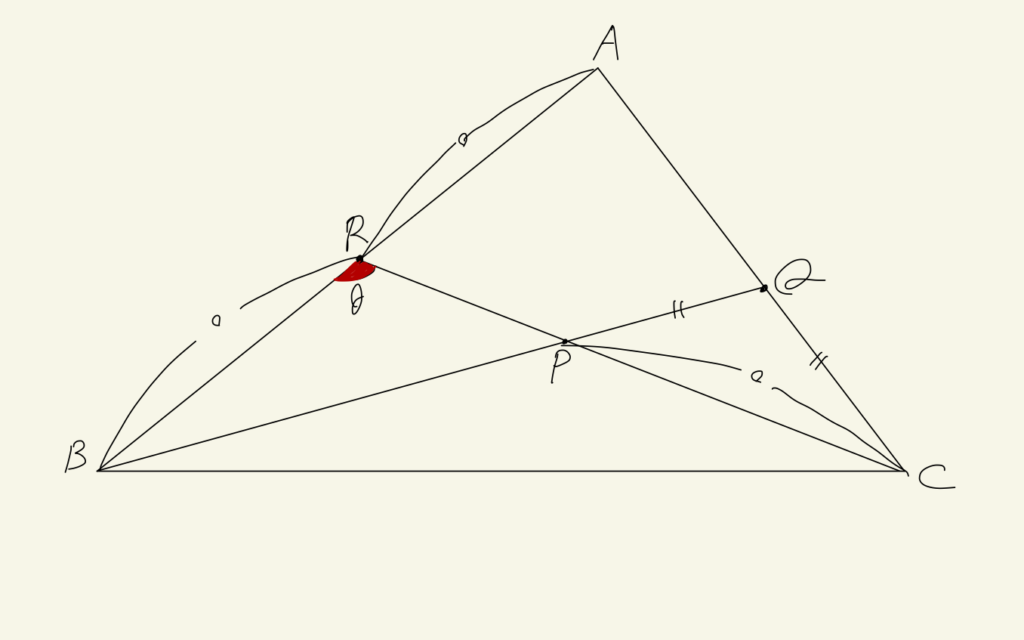
メネラウスの定理を適用します。二通りありますが、次のように使います。
$$\frac{RA}{BR}\cdot\frac{CQ}{AC}\cdot\frac{PB}{PQ} = 1$$
ここで、RA=BR, CQ=PQであることからPB=ACと求められます。次に補助線を引きます。初等幾何では補助線を引くのが醍醐味です。
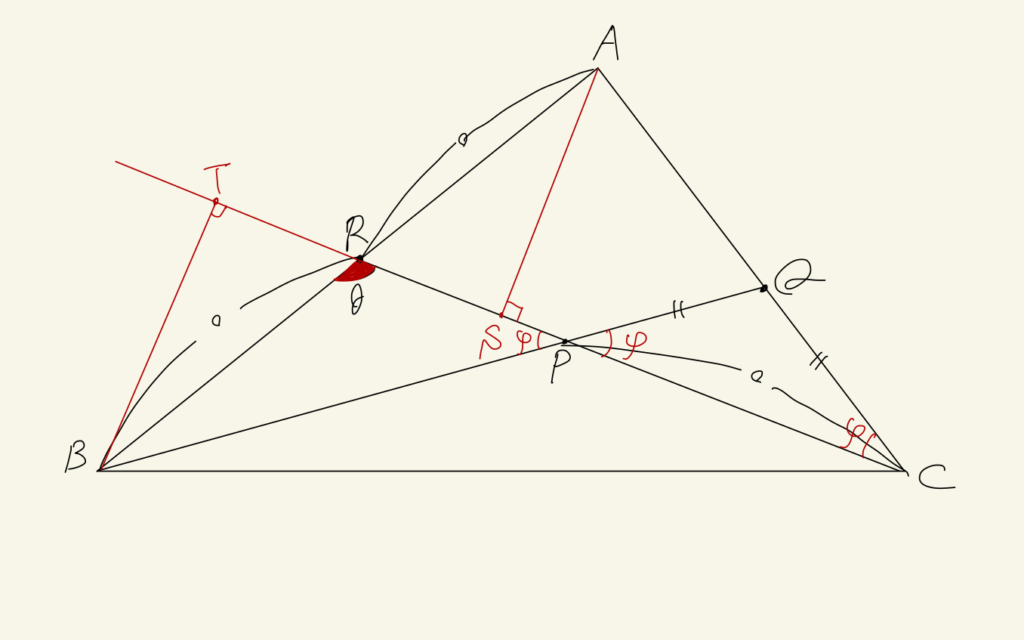
$$TP = BP\cos{\psi},\ CS = AC\cos{\psi}$$
今∠ACS = ∠BPT、AC = BPよりTP=CS.
$$TS = TP – SP,\ CP = CS – SP,\ TS = CP = AR$$
また、三角形TRBと三角形ARSは合同なので、TR = SRであり、先の関係式からAR = 2RS.また補助線の引き方から∠ASR = 90°であり、∠ARS = 60°とわかる。ゆえに求める∠BRC = 120°。
あまりにも綺麗なのでこれで良いのか疑うほどです。もし、不備・誤りを発見されたらご指摘いただくと助かります。よろしくお願いします。
オリンピックらしい問題と言えば、このような記事もどうぞ!

コメント