自問
中学生・高校生が夏休みに行う数学自由研究の題材って何だろう?
自答
受験生を除くと、学校によっては数学に関する自由研究を考える宿題がありますよね。理科系ならまだしも、数学の自由研究なんてピンとこない、という方は多いのではないでしょうか。しょうがないから、数学に関係しそうな話をネットからかき集めてレポートにする、という人も多いのではないのでしょうか。
しかし、どうせなら、ある程度「研究」の名に恥じぬよう「オリジナル」の題材を考えたいという人もいるのではないでしょうか。そういう意欲的な方の助けになるような記事を書いていきたいと思います。アイデアが思い浮かべば、その都度この記事を更新していきたいと思います。とりあえず、今すぐ思いつくものを挙げていこうと思います。
自由研究課題1 〜 必勝法の存在するゲームの発案 〜
数取りゲーム

14

13, 12, 11

10

9

8, 7, 6

5, 4

3, 2

1

僕の勝ちだね。
僕が中学生の頃に、暇つぶしの時にやっていたゲームです。このゲームは実は先手必勝のゲームです。どのように戦略を組めば良いでしょうか。それほど難しくないので考えてみると良いと思います。さらに、これを自由研究のテーマとする場合には、このゲームを次のように一般化して必勝法の有無、戦略の立て方を議論するのが良いでしょう。
拡大版○×ゲーム
○×ゲームと言えば、3×3のマス目に二人が交互に○や×を書いていって、どちらかの記号が縦・横・斜めのいずれかで3連続すれば勝利となるもので、よく知られていると思います。このゲームでは、必勝法は存在しないことがわかっています。すなわち、先手・後手どちらも最善の手を指せば引き分けです。
それでは、マス目の数を増やして5×5にしたらどうでしょうか。この場合は手の数が飛躍的に増加します。それで少しルールを変更して、どちらかの記号が縦・横・斜めのいずれかで4連続または5連続すれば勝利するとしたら、先手・後手のいずれかに必勝法は存在するでしょうか(3連続では明らかに先手必勝です)。私は考えてみたことはないですが、時間があれば興味深いテーマだと思います。
ちなみに、縮小版オセロゲーム(4×4や6×6)では必勝法が存在することが証明されています。4×4などは自分の手で調べてみるのも面白いですね。
自由研究課題2 〜 集団の平均値予想と学力レベル 〜
こんな問題(ゲーム)がある。
自由研究課題3 〜 ラノベと文学作品を見分けるパラメータの探索 〜
文学作品といえば、初等教育の国語の教科書にも載るような夏目漱石、森鴎外、志賀直哉、島崎藤村、兼好法師、清少納言などの作品を指します。ライトノベルとは、皆さんもよくご存知とは思いますが、有名どころでは「涼宮ハルヒの憂鬱」や「とある科学の禁書目録」などでしょうか。例えば、人間が文学作品とライトノベルを同時に見れば、それらを見分けることはたやすいでしょう。
それでは、機械にこれらを見せた時、機械は二つの種類を見分けることができるでしょうか。「そもそもそんな必要ない」という意見は置いておきましょう。人間ならなんとなくその性質から物事を見分ける定性的な判断ができますが、機械にはできません。機械がものを判別する際には、何らかの「定量的な」ものが必要で、パラメータと呼びます。今大流行りのDeep learningというのはまさに「定性的なもの」をデジタル情報に変えてしまい、そこからものを見分ける「パラメータ」を抜き出し、それを元に情報を分類するということをやっています。
もし、文学作品とライトノベルを区別するパラメータが見つかれば、そのパラメータの値に応じて文学作品とライトノベルを識別することができるかもしれません。イメージとしては次のような分布が得られれば、成功です。
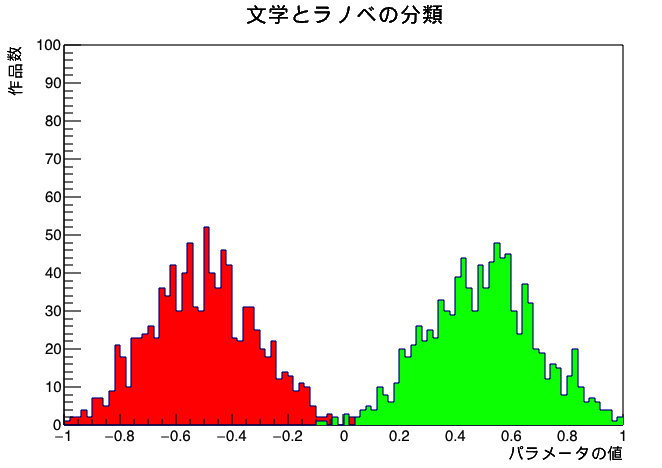
2. 全体の文の数に対する「セリフ」の割合
3. 1文1文の文章の長さ
自由研究課題4 〜 トノサマバッタの生息数 〜
対象
- 対象:中学生以上
- 応用範囲:大
- 難易度:上級
概要
このタイトルは、10数年前に某都立高校の推薦入試問題で出題された問題のテーマとなったものです。問題では、原理を数学的な確率計算で確かめさせてから、その応用として「トノサマバッタ」の生息数を求める方法を考察させていました。統計手法としては非常に有名な方法で「捕獲-再捕獲法」と呼ばれる手法です。母集団の数がわからないものを統計的に推定することができます。
原理
例えば次のような問題を考えましょう。
この手の問題は、中学入試でも出題されることがあり、その意味で中学生以上なら誰でも理解できるはずです。一回一回の事象がランダムであることを前提としているので、「確率」の考え方で解くことができます。
箱の中にあるボールの数をNとします。1回目の試行でn個のボールにマーキングをしているので、マーキングをしたボールを取り出す確率はn/Nです。次に2回目の試行でM個のボールの中にa個のボールがマーキングされていたことを考えると、マーキングを施したボールを取り出す確率はa/Mです。
さて、ここが問題です。確率としては厳密にn/N=a/Mが成り立つとは限りませんが、”推定”という観点からこの二つの確率は等しいものと考えることができます。ゆえにNは
$$N = \frac{Mn}{a}$$
と推定することができます。この試行を何度も繰り返してその平均をとれば、推定値は実測値に近づいていくことがわかると思います。
研究方法
N, Mを色々変えて、推定値と実測値の差を見てみるというのも面白いと思います。予想として、N, Mが大きければ大きいほど推定値と実測値の差は小さくなることが予想できます。
- 母集団が相当数である。
- 母集団がある一定の領域内にランダムに分布しており、捕獲、再捕獲時にその数が変化しない。
- サンプル(選ぶもの)をランダムに捕獲、再捕獲できる。
このような条件を満たす事象を見つけることができれば、捕獲-再捕獲で母集団の数を推定することができます。実生活に応用しようと思うとき、おそらく厄介なのは条件2です。これをうまくクリアできるものを考えることが重要でしょう。
自由研究課題5 〜 モンテカルロ法による推定 〜
対象
- 対象:高校生以上(原理を確実に理解したいなら大学生、とりあえずやってみるだけなら中学生でも可)
- 技術:数値計算でシミュレーションを行いたい場合はプログラミングの知識(初級程度)
- 応用範囲:大
- 難易度:上級
概要
モンテカルロ法は数値計算やシミュレーションを通じて、ある事象に対する近似解を求める手法のことです。具体例として、円周率を求めることが有名である。”モンテカルロ 円周率”としてググれば、様々なサイトで丁寧な解説が行われています。ここではモンテカルロ法の詳しい説明は省き、簡単な原理の説明をすることにします。
原理
モンテカルロ法では「乱数」を用います。算数、数学において確率の問題を解くとき「一様に」とか「ランダムに」とか、その類の言葉が使われますが「乱数」はこのランダム性と深い関係があります。特にモンテカルロ法では「一様乱数」というものがよく使われます。例えば、0から1までの全ての実数、というと無限個の数がありますが、この中で全ての数を等しい確率で取り出したときの数を「一様乱数」と言います。サイコロの一様乱数とは、1から6の中の目を全て等しい確率で取り出したものと言えるでしょう。一様乱数を人間が作り出すことはほとんど不可能で、実は、機械でさえも完全に一様の乱数を作ることは極めて困難です。しかし、機械であれば限りなく一様乱数を作ることは可能で、実際にそのようなプログラムを実装したサイトはあちこちに見られますし、プログラミングの世界では一様乱数を生み出すコードが日々開発されています。一様乱数を用いて、例えば円周率を求めることができます。
- 原点と中心が重なるように半径1の四分円を書く。
- 0から1までの一様乱数を2個1組みで取得して座標(x, y)を定義する。
- N組の座標を取得して、それぞれに対応する点が四分円の中にある組みをn組とする。
- 4n/Nが円周率の推定値である。
1については次のような図があるとわかりやすいでしょう。
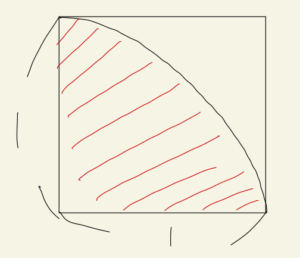
2の一様乱数で取得した値をx, y座標に持つ点A(x, y)が四分円の中に入る確率Pは四分円の面積と正方形の面積で決まるはずなので、
$$P=\frac{\pi}{4}$$
です。3, 4で求められた値n/Nは、まさに点Aが四分円の中に入る確率なので
$$\frac{n}{N} = \frac{\pi}{4},\ \pi = \frac{4n}{N}$$
と計算できるわけです。
研究方法
モンテカルロ法を用いると例えば次のような問題を解くことができます。
$$S = \frac{nAV}{N}$$
となる。
自由研究課題6 〜 衝撃破壊の統計則 〜
対象
- 対象:高校2年生以上(対数を学んでいるなら高校1年生でも)
- 知識:対数や正規分布の知識
- 実戦応用範囲:大
- 難易度:上級
概要
衝撃破壊というのは、読んで字のごとく衝撃を与えて物体を破壊する、ということです。このとき、破壊されて粉々になったものにはある統計則が成り立つ、というのです。これは、つまり、ガラスのコップを床に落としてバラバラに破壊した時、そこにある法則がある、と言っているわけです。とても不思議な話ですよね。
原理
この法則を説明する前に、二つの概念を説明しておく必要があります。それは「べき乗分布」と「正規分布」です。そもそも「分布」というのは何なのかをおさらいしておきましょう。「分布」は高校生でも「ヒストグラム」という形で学んでいますが、現在の日本の高校数学の教科書には「統計」を学ぶ機会がほとんどないので、分布は聞きなれない言葉だと思います。分布をわかりやすくいうと、次のようなものです。
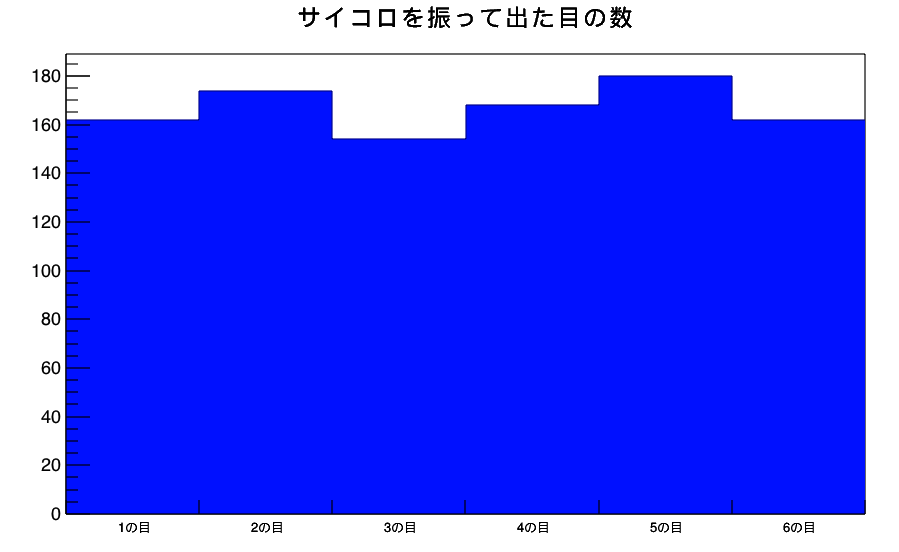
$$Y = cX^{-a}\ (a>0)$$
例えばc=1, a=-1の時はY = 1/Xとなり、反比例のような分布になります。
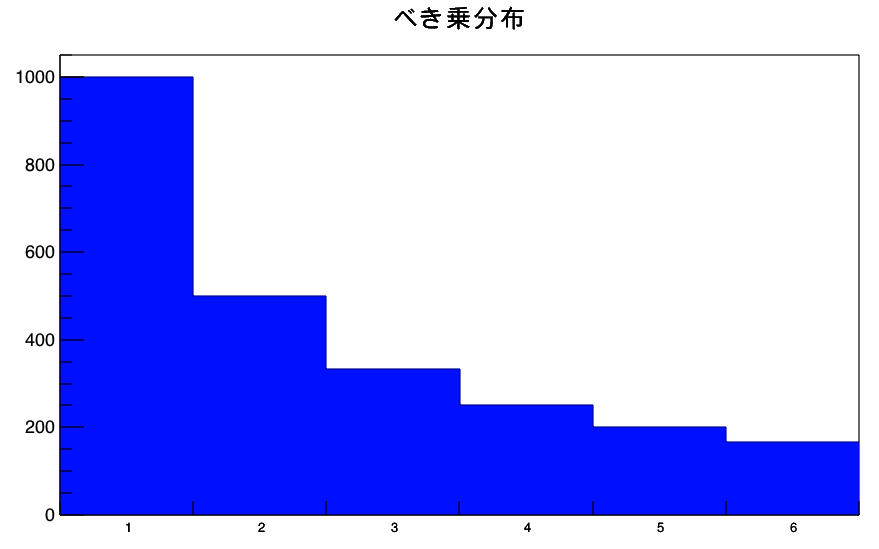
$$Y = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-{\frac{(X-\mu)^{2}}{2\sigma^{2}}}\right)$$
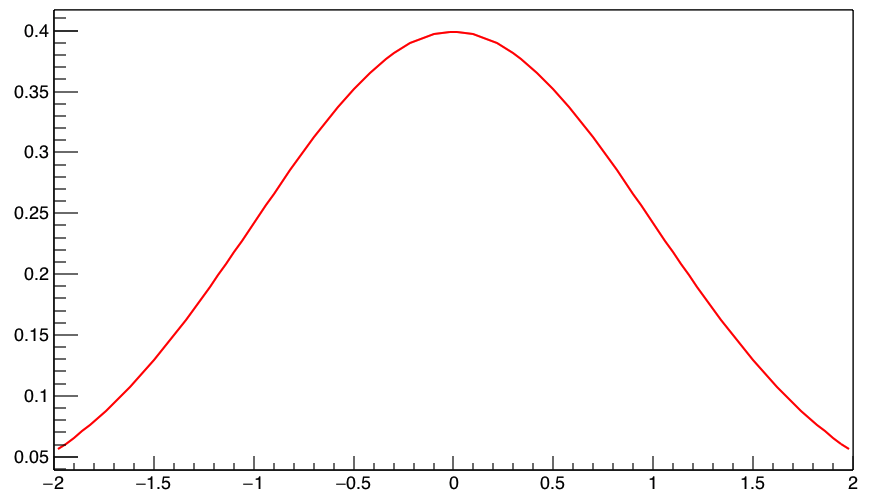
このように正規分布は、μ(この場合は0)を平均として左右対称に、σ(この場合は1)の幅で分布します。σを大きくするほどなだらかな山、σを小さくするほど急な山になります。正規分布は別名、ガウスの関数(ガウシアン)です。ガウスというのはあの有名な数学者のことですね。正規分布はその名前の通り、”ありふれた分布”であり、将来物理学の研究に携わるようなことになれば、年がら年中お目にかかる分布でしょう。物理だけでなく、日常生活の至る所でも現れる分布です。ところで、正規分布と似たものとして、対数正規分布というものがあります。
高校数学の範囲内では横軸も縦軸も1, 2, 3, …という等間隔の幅の座標を使います。化学ではたまに出てきますが、横軸または縦軸を「対数」にするような場合があります。対数正規分布では横軸を対数に変えて分布を作ったときに、分布が正規分布の形をしているもののことを言います。
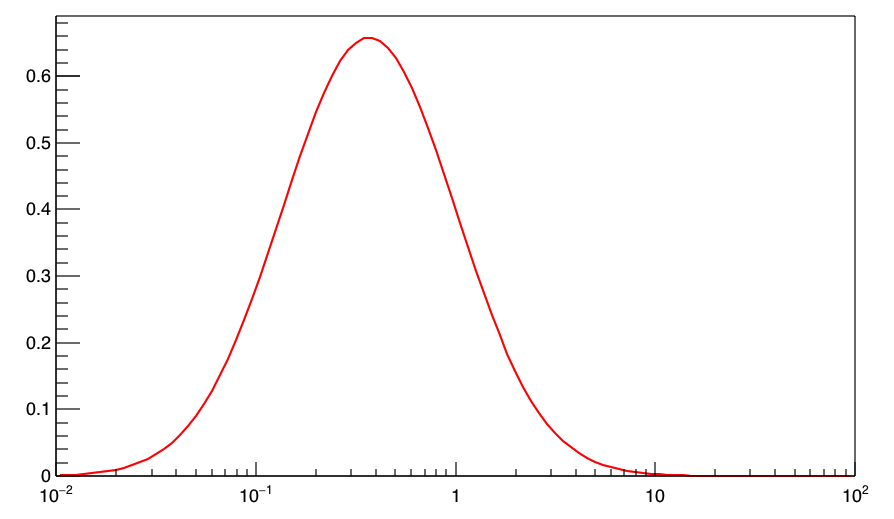
ちなみに対数正規分布は次の式に従います。
さて、べき乗分布と正規分布の導入が終わったところで、本題に戻ります。衝撃破壊の統計則とは一体何なのか。
この統計則は、衝撃によって粉々になった破片をサイズごとに分類してヒストグラム(分布)を作ると、べき乗分布や対数正規分布になるという主張である。こんなこと、凡人は知らなければ夢にも思わないことですが、実際に理論を構築して、実験結果と照らし合わせた偉大な数学者がいるというのは、驚きです。
研究方法
まず、一つのテーマとして、統計学を勉強するというのは非常に重要な自由研究だと思います。なぜなら、理系に進んでも文系に進んでも、大学生活で研究をしようと思ったら「統計学」は必須の学問ながら高校ではほとんど学ぶ機会がありません。また、教養として身につけておいて、テレビの安易なアンケート結果などに騙されないようにするというのは重要です。ここで取り上げたような正規分布や、その前の実験テーマで紹介した「精度の評価」などをテーマにするのも良いと思います。
しかし、それにもまして魅力的なのは、実際にものを壊して分布を作るということでしょうか。衝撃破壊、というのはやり方を誤ると非常に危険ですので、もしこれを自由研究のテーマに選ぶ場合は一人でやるのは危険でしょう。理科の先生と相談するか、両親と相談して、安全に実験をできる環境を作ることが大切です。
しかし、物体によって、破砕の質量または長さがどのような分布になっているかを自分の目と手で確かめるというのは非常に興味深く、魅力的なテーマであると思います。
また、この統計則は「衝撃破壊」だけでなく、他のケースにも成り立つことだと言われています。
実際に調べた人がいるというのも驚きですが、複数のテキストを選んできて、文章の長さを数え、それが登場した回数を分布にした時、「文章の長さ」の対数を横軸にとり、回数を縦軸にとった分布は近似的に、対数正規分布となったそうです。
このように、発想次第では、誰も知ることがない隠れた正規分布を見つけることができるかもしれません。
終わりに
もし、興味があるものがあればご自由に題材をとっていただいて構いません。もし結果が出たらダイジェストでも教えてくれると嬉しいです。また、それぞれのテーマに興味があるが、いまいちよくわからない、ということであればコメントしていただければお答えします。
そんなに凝った自由研究をやる時間がない、という方には、こちらの記事をどうぞ。
短時間で仕上げる! 自由研究(数学)のテーマを中学・高校の各学年に対応して考えてみた
また、本ブログでは最近、統計学を利用した簡単な研究記事を公開しました。
Bayesian(ベイジアン)とFrequentist(頻度論者)の立場からカイジ「地下チンチロ」に登場した四五六賽を研究する

コメント