高校入試における「放物線」
高校入試では、次のような問題セットになることが多いです。
- 小問集合
- 放物線の問題
- 平面図形の問題(合同や相似の証明を含む)
- 立体図形の問題
- 規則性に関する問題
公立高校においては都道府県ごとに共通問題を使用する学校と「適性検査」や「自校作成」という形で高校独自の問題を課すことがあります。特に「高校独自の問題」を課す高校では、問題によって難易度がまばらで、特に「規則性に関する問題」や「立体図形の問題」は難化する傾向があります。
しかし、放物線の問題はパターンが非常に限定されており、対策がしやすいばかりか、中学数学限定で使用できるテクニックがあり、これらを用いて「短時間」でかつ「高得点」が狙える分野です。高校独自の問題を作る高校で、国語・数学・英語・理科社会のうち、英語はとても得意だが数学はまるでだめ、という生徒の場合、数学は「小問集合」と「放物線」を全力で取り組み、ほぼ完答できさえすれば他がまるでダメでも英語で取り返せることがあります。そういう意味で、数学が苦手な生徒は夏休みに「放物線」に全力を向けて対策をすることが、志望校合格の近道と言えるでしょう。
中学数学での放物線の復習
中学数学では放物線は次の式で表される関数です。
$$y=ax^{2}$$
ここでaは実数です。グラフではaの値に応じて次のように描けます。
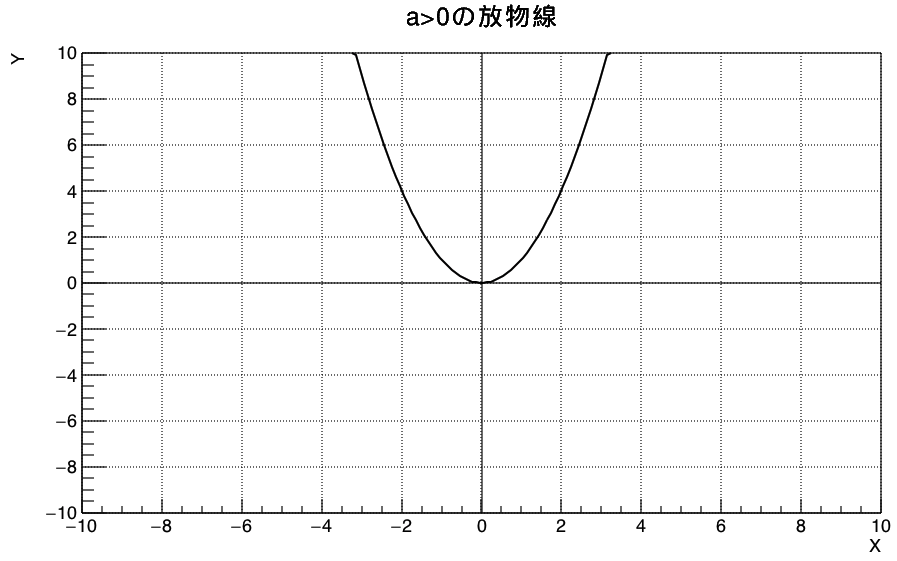
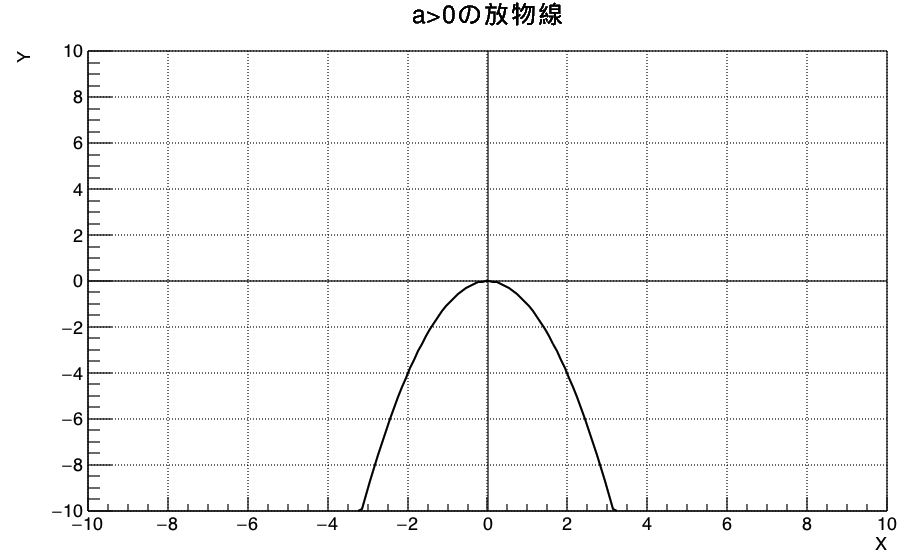
aの値は、グラフのメモリを読み取れば求められますね。例えば、上のグラフでは(2, 4)を通っているので次のようにa=1とわかります。
$$4 = a \times 2^{2} \leftrightarrow a = 1$$
詳しくは学校のテキストに譲りましょう。
放物線の問題の典型的な解き方
典型的な問題
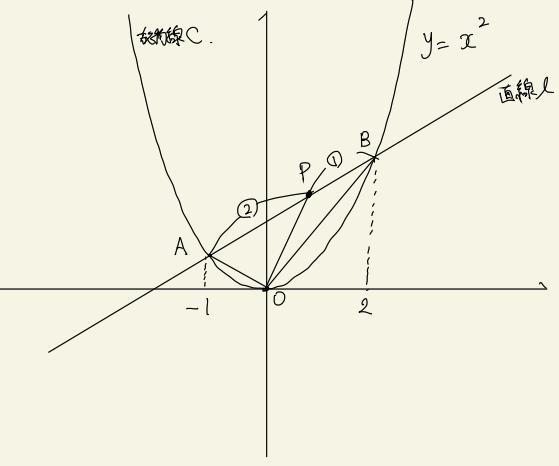
問1. 直線lの式を求めよ。
問2. 点Pの座標を求めよ。
問3. △OPBの面積を求めよ。
典型的な解き方
問1
点A, 点Bのy座標をそれぞれyA, yBとすると\(y_{A} = (-1)\times(-1) = 1,\ y_{B} = 2\times2 = 4\)です。これらから傾きaを求めると
$$a = \frac{4-1}{2-(-1)} = 1$$
直線の切片をbとすると\(y=x+b\)より、(2, 4)を代入すると\(4=2+b,\ \leftrightarrow\ b=2\)となり、求める直線の式は\(y=x+2\)である。
問2
下の図を用います。
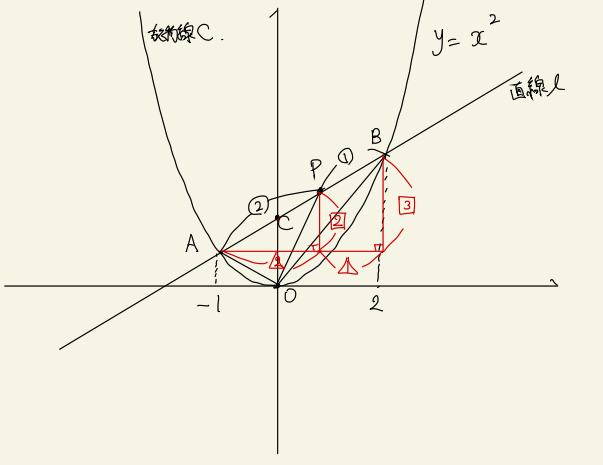
上のように三角形を作って比を使うと、点Bと点Aのx座標の差は3ですので、これを2:1に内分する点Pのx座標は-1+2 = 1となります。また点Bと点Aのy座標の差は3ですので、これを2:1に内分する点Pのy座標は1+2 = 3となります。よって点Pの座標は(1, 3)です。
問3
△OABの面積を求めて、1/3をかければ良いでしょう。△OABの面積は△OCAの面積と△OCBの面積の和として計算できます。
$$△OCA = \frac{1}{2}\times1\times2 = 1,\ △OCB = \frac{1}{2}\times2\times2 = 2$$
$$△OAB = 3,\ △OPB = 3\times{1}{3} = 1$$
放物線や座標平面の問題で習得すべき重要なテクニック
さて、ここからがこの記事の本番です。上の典型的な問題と連動して3つのテクニックを紹介します。
$$S = a(p+q),\ I = -apq$$
なぜ、このような式で表せるか考えてみましょう。先ほどと同じくA, Bのy座標をyA, yBとするとそれぞれ\(y_{A} = ap^{2},\ y_{B} = aq^{2}\)です。直線Lの傾きSは
$$S = \frac{aq^{2}-ap^{2}}{q-p} = \frac{a(q+p)(q-p)}{q-p} = a(p+q)$$
です。このことから直線Lを\( y=a(p+q)x + b \)と置くことができて、ここに\((p, ap^{2})\)を代入すると
$$ap^{2} = a(p+q)p + b \leftrightarrow b = -apq$$
以上より、上のテクニックが正しいことが示されます。塾に通っている生徒やちょっと気の利いた先生がいる学校では、当然のように学ぶものですが、意外と知らない生徒も多いので使えるようにしておくと大変便利です。またこの公式を逆に使うこともできます。というのは、学校によっては直線の傾き、A, Bのx座標を提示しておいて、放物線のaを求めさせる問題もあります。その場合にもこの公式を利用することができます。とにかく色々な問題に対して、「素早く」「正確に」解くチャンスを与えてくれるので、何としても身につけておきたいものです。
$$P_{x} = \frac{nx_{1}+mx_{2}}{m+n},\ P_{y} = \frac{ny_{1}+my_{2}}{m+n}$$
式で書くと面倒に見えますが、考え方は「たすき掛け」の要領です。
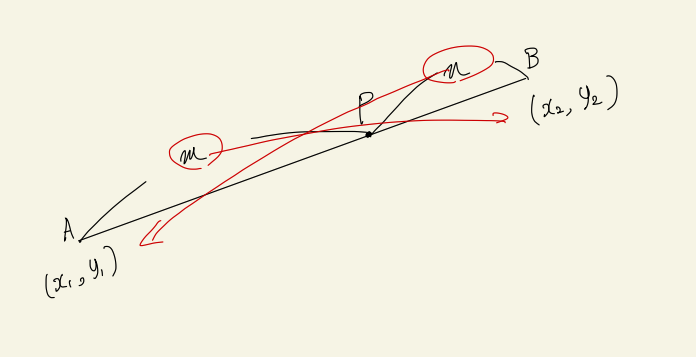
上の図のように、A側との積はnとペアを組み、B側との積はmとペアを組みます。分母は単純にm+nで良いです。これを使うと補助線だの相似だの使わなくても解けるので便利です。実は高校2年で学ぶことですが、中学生でも使う分には問題ないでしょう。
証明はしませんが、高校生でも知らない人がいる公式です。”外積”という考え方を用いますが、三角形の面積の計算過程など、自校作成などの「記述」のなかに入れる必要がないので、この公式は身につけておいて損はありません。
テクニックの適用例
それでは具体的にこれらのテクニックを先ほどの典型問題に適用します。
問1
直線の式はy=a(p+q)x-apqであり、a=1, p=-1, q=2より
$$y=x+2$$
問2
点Pは点A(-1, 1), 点B(2, 4)を2:1に内分する点なので
$$P_{x} = \frac{2\times2+1\times(-1)}{2+1} =1 ,\ P_{y} = \frac{2\times4+1\times1}{2+1} = 3$$
より点P(1, 3)
問3
点P(1, 3), 点B(2, 4)より△OPBの面積Sは
$$S = \frac{|1\times4-3\times2|}{2}=1$$
あっという間に解決しますね。放物線問題では、これらのテクニックを駆使して問題を解くことが重要です。また、この記事であげたテクニックは非常に基礎となるものであり、放物線関連には他にも身につけておくべきいくつかのパターンがありますので、近いうちにそれらも紹介してみたいと思います。よろしければ参考にしてみください。

コメント