この記事では、統計学を考える上で重要な二つのスタンス「Bayesian」と「Frequentist」の違いを考察した上で、特にBayesianの考え方を応用して、漫画(アニメ)カイジの「地下チンチロ」を主題とした研究(の真似事)を行ってみたいと思います。Bayesianの解析においては、Bayes(ベイズ)の定理を多用しますので、Bayesの定理にあまり馴染みがないという方は、ぜひ、こちらの記事も合わせて読んでいただけると嬉しいです。
モンティ・ホールのパラドックスを例に、Bayes(ベイズ)の定理の使い方と考え方を考察する
イントロダクション:分布とは
分布を簡単に説明すると、「ものの散らばり具合をグラフや数式で表したもの」という感じでしょうか。例えば、日本の都道府県別の人口「分布」というと、次のようなものをいいます。
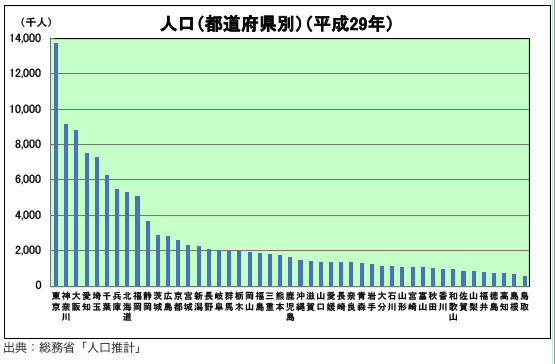
横軸を各都道府県、縦軸をそれぞれの都道府県に住む人口の数を棒グラフにしたものです。このように、分布をグラフにしたものを「ヒストグラム」と呼ぶことがあります。この記事でもヒストグラムという言葉を使っていきます。
より数学的な例を使うなら、サイコロを何回か振って、出た目の回数を縦軸にしたものがあります。
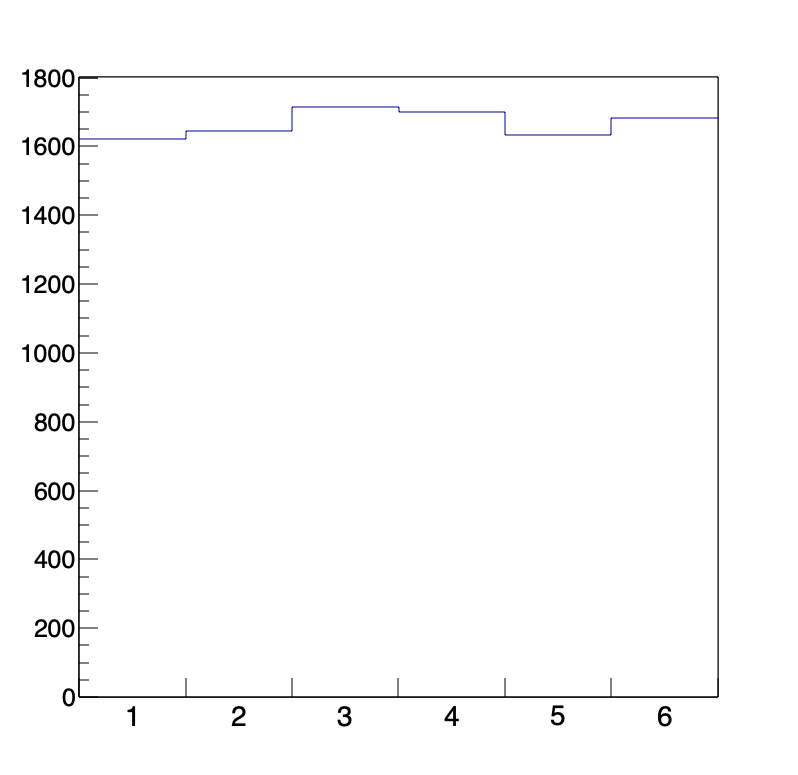
上のヒストグラムは、横軸をサイコロの目、縦軸を10000回サイコロを振ったときそれぞれの目が出た回数を表したものです。もし、サイコロの目が出る確率が同様に確からしいとするならば、サイコロの目が出る回数は、ある分布に従うことがわかっています。想像できる通り、上のヒストグラムはサイコロを投げる回数を増やせば増やすほど、よりフラット(平ら)になっていきます。このような分布のことを「一様分布」と呼びます。一様というのは、「どれも同じ」という意味合いを持つのでまさしく「どの場合も同じ回数だけ起こる」という現象を表しています。もちろん、現実ではどの目も均等に出るという保証はありませんが、理論上は「サイコロの目が出る回数はある分布に従う」ということができます。このように、現実の現象を理論に適用させるときには、「現象がある分布に従う」という表現がよく使われます。
同じような例では、正しいコイントスであれば、裏が出る回数、表が出る回数の分布は一様分布に従います。同じコイントスであっても、別の現象を考えることができます。例えば、10回コイントスを行い、表が出た回数をX回とします。10回のコイントスを何回か行ったとき、横軸をXとして縦軸を表がX回出た回数にしたヒストグラムを作ると、これはある分布に従うことがわかっています。試しに、これを10000回やってみると、次のようなヒストグラムを得ます。
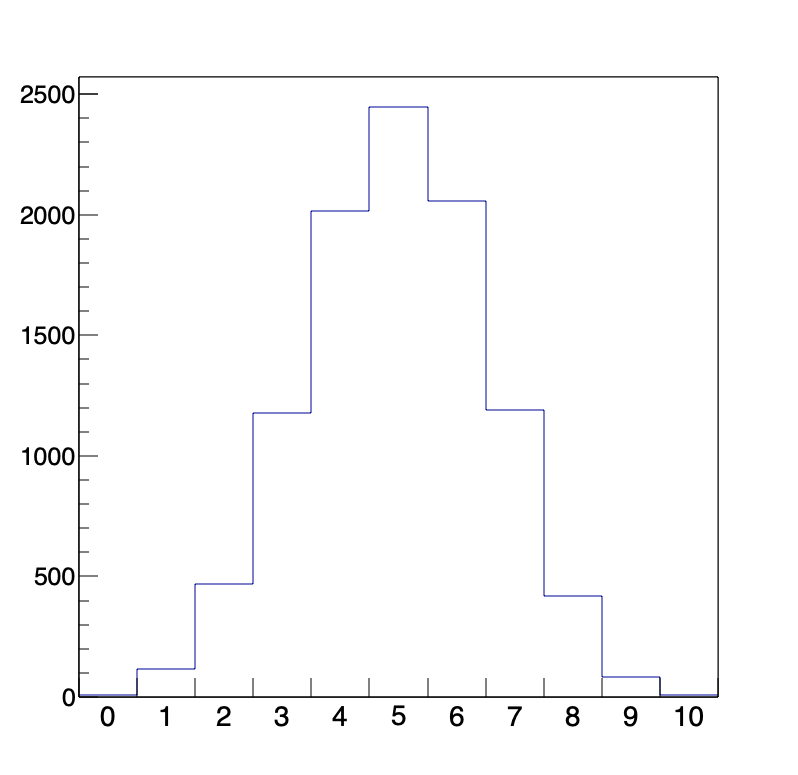
今度は一様分布ではなく、10回のコイントスのうち、表が5回出る回数がもっとも多く、他の場合は左右対称になるような形をしています。この形は、それぞれの場合が起こる確率を反映しています。というのも、10回のコイントスで表がそれぞれX回出る確率というのは、以下のように計算できます。
表が0回の時は、
$$\left( \frac{1}{2} \right)^{10} \times _{10}C_{0} = \frac{1}{1024}$$
表が1回の時は
$$\left( \frac{1}{2} \right)^{10} \times _{10}C_{1} = \frac{10}{1024}$$
表が2回の時は
$$\left( \frac{1}{2} \right)^{10} \times _{10}C_{2} = \frac{45}{1024}$$
表が3回の時は
$$\left( \frac{1}{2} \right)^{10} \times _{10}C_{3} = \frac{120}{1024}$$
表が4回の時は
$$\left( \frac{1}{2} \right)^{10} \times _{10}C_{4} = \frac{210}{1024}$$
表が5回の時は
$$\left( \frac{1}{2} \right)^{10} \times _{10}C_{5} = \frac{252}{1024}$$
さらに、表が6~10回出る確率というのは、”C”の性質からそれぞれ表が4~0回の確率と一致します。このように確率を計算したものをヒストグラムにすると次のようになります。このとき、縦軸を「確率」に置き換えて表します。
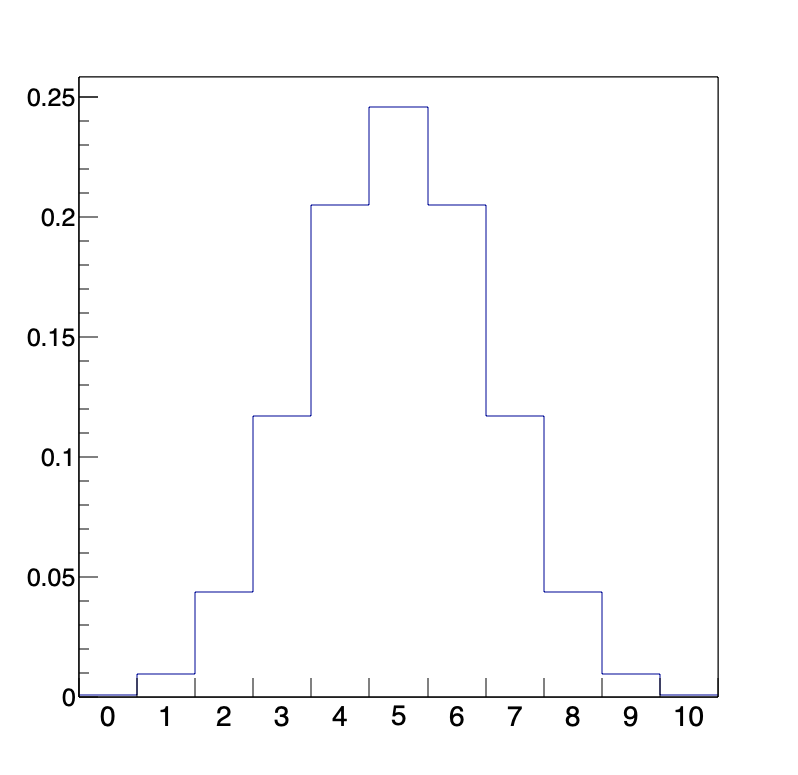
実際にコイントスを行った場合は、形だけをみるとかなり似ているように思いますよね。さて、コイントスのように「表」か「裏」の2通りしか起こらない状況で、どちらか一方がX回起こる回数を縦軸にした分布を「二項分布 (binomial distribution)」と言います。二項定理という言葉に含まれる「二項 (binomial)」と同じ言葉です。二項分布では、二つの事象が起こる確率は等しい必要はありません。例えば、表が出る確率が20%のコイントスを行ったときに、上と同じような方法でヒストグラムを作ってみます。
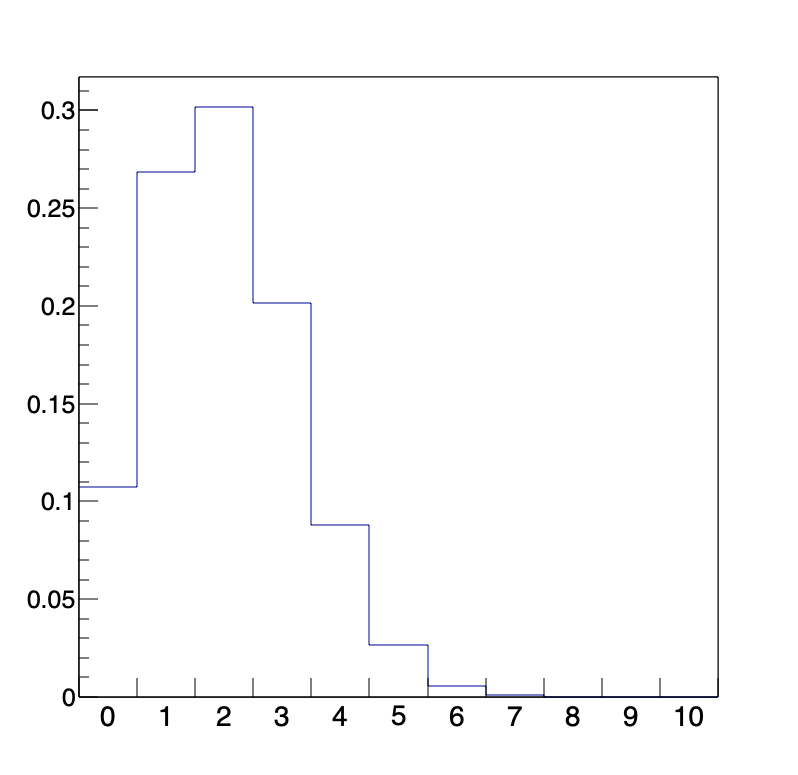
このように、今度は表が2回出る回数がもっとも多くなるという結果になりました。これも二項分布の一種です。二項分布は、コイントスを行う回数、1回のコイントスで表や裏などの事象が起こる確率によって、それぞれ異なる形を持っているというのが特徴です。
今までの分布は、横軸が実数として飛び飛びの値を持つ「離散量」を用いて考えてみましたが、分布の中には横軸が一続きの連続した実数となる「連続量」を用いたものがあります。連続量を用いた分布の中で、もっとも有名なものは「正規分布」だと言って良いと思います。その名の通り「ありふれた分布」です。正規分布は次のような形をしています。
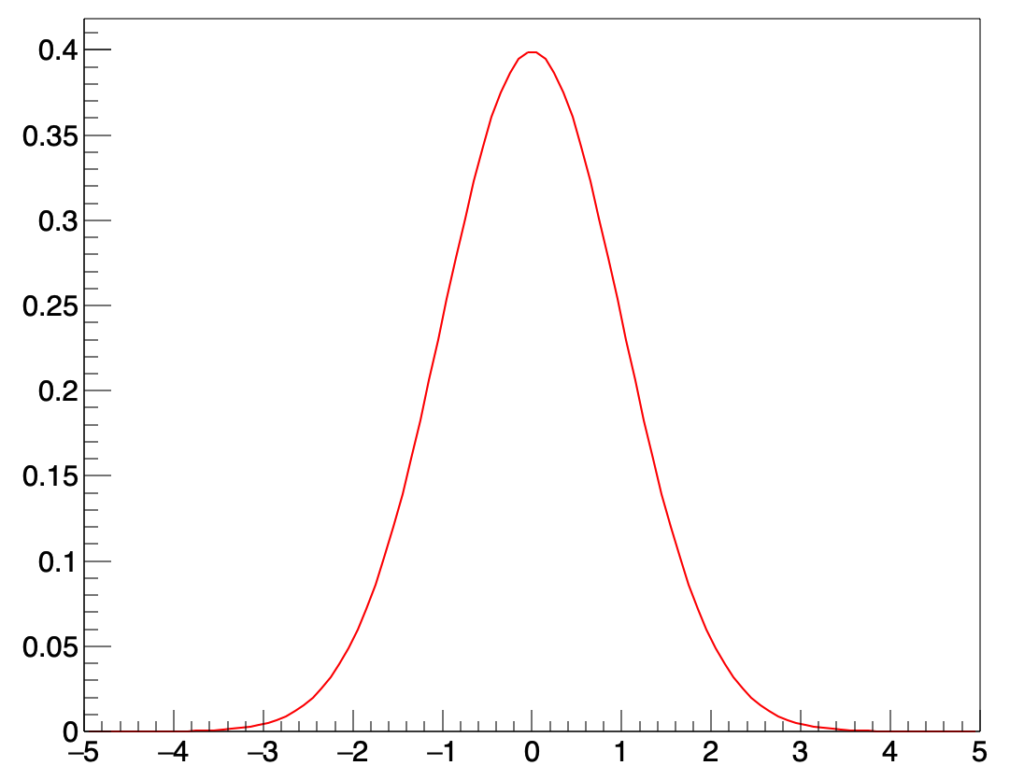
正規分布の定義域(\(x\)の範囲)は\(-\infty\)から\(\infty\)までですが、ここでは形をわかりやすくするために\(-5\)から\(5\)までをピックアップしています。この図から一般化できることは、正規分布はある値を軸にして左右対称な形をしている、ということです。上の図では0を軸にしていますが、0以外を軸とすることもできます。また、正規分布のパラメータの振り方を変えると、よりなだらかな山にすることもできますし、より急な山に変えることもできます。正規分布のパラメータは2つで、それぞれ\(\mu, \sigma\)と書くことが多いです。\(\mu\)が軸の位置、\(\sigma\)が山のなだらかさを表します。この二つのパラメータに注目して正規分布の一般形をみてみます。
$$\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-{\frac{(X-\mu)^{2}}{2\sigma^{2}}}\right)$$
一見すると複雑な形をしていますが、上のグラフのように\(\mu=0, \sigma=1\)としたものを考えると
$$Y = \frac{1}{\sqrt{2\pi}}\mathrm{exp}\left( -\frac{X^{2}}{2} \right)$$
と書くことができます。こうみると、高校数学で学ぶ関数の範囲内で十分理解できるものだとわかります。expというのは、exponentialの略で\(exp(-x^{2}) = e^{-x^{2}}\)という意味です。また\(\mu\)を平均、\(\sigma\)を幅と呼ぶことがあります。
正規分布の例としてよく用いられるのは、X軸を身長にしたときその身長をもつ人口の人数をY軸にしたものです。このヒストグラムは、考えている全ての人間の身長の平均を軸とする正規分布に近いものになっています。
他にもべき乗分布(指数分布)やポアソン分布など、有名な分布がありますが、大学に入って研究活動をしたいと思っている方は早めにこれらの分布を理解して、その応用方法を知っておくと非常に有利になると思います。
BayesianとFrequentistとは
Bayesian(ベイジアン)とFrequentist(頻度論者)は統計学の問題を解釈する2種類の大きな派閥と言えます。本質的に同じものを扱いながら、それぞれのスタンスで異なる解釈をするという、まるで宗教の派閥に近いものがあると思います。例えば、ある人がコインを20回振って、そのうち15回だけ表が出たとします。ここで、Bayesianの人はこんな風に考えます。
【相手がイカサマコインを使っているとすると、今までのデータから考えて、そのコインが表が55%~95%の確率で出るイカサマコインである確率は、95%である】
一方、Frequentistの人はこんな風に考えます。
【そのコインは75%の確率で表が出るイカサマコインだとすると、さらに100回コインを振れば、表が出る回数が55回以上95回以下である確率は95%である】
これらの違いを端的に表すなら、Bayesianはパラメータに関する「測定データ」から出発して「真の値」を推定。Frequentistはパラメータの「真の値」から出発して「測定データ」を「推定」していると言えます。今の場合に即して言い換えると、Bayesianは相手がイカサマコインを使っている可能性、使っていない可能性など全ての可能性を考慮して、データに即して計算を行ったときに、そのコインがイカサマコインである確率を推定しています。Freqentistは相手がある特殊なイカサマコインを使っていることを仮定してデータを分析したとき、次に起こるデータがどれくらいになるかを推定しています。
「20回中15回だけ表に出たということは、表が出た確率は75%。正しいコイントスなら50%で出るはず。よってお前はイカサマコインを使っだだろう!」というのは、正しいコイントスとそのコイントスに含まれる誤差(偶然性)を考えて、表がでる確率が75%というのはその誤差をはるかに超えているからお前はイカサマをした、という思考回路です。これはFrequentist的であると言えます。では、Baysian的には、どのように考えていくのか、を考察していきます。
まず、ベイズの定理を書き下します。
$$P(H|D, I) =\frac{P(H|I)P(D|H, I)}{P(D|I)}$$
ここで、それぞれの記号が表していることをまとめます。
・P(A|B) : Bというイベントが起こることがわかっているときに、Aというイベントが起きる確率(条件付き確率)
・\(H\) : ある仮説。
・\(D\) : データ。
・\(I\) : 前提知識。
・\(P(H|D, I)\) : データ(D)と前提知識(I)を仮定したときに、その仮説が正しい確率。
・\(P(H|I)\) : 前提知識を仮定したときに、その仮説が正しい確率
・\(P(D|H, I)\) : 仮説と前提知識を仮定したときに、そのデータが生じる確率。
・\(P(D|I)\) : 前提知識を仮定したときに、考えられる全ての仮説の下でそのデータが生じる確率を足し合わせたもの(規格化因子ともいう)。
ベイズの定理に、先ほどのコイントスの例を適用させてみます。そのとき、H, Dは次のように対応させることができます。
\(H\) : コインが\(p\)の確率で表が出る
\(D\) : コインを20回投げると15回表が出た
それでは、\(I\)(前提知識)とは何でしょうか。この前提知識こそBayesianの強みでもあり、また難しいところでもあります。仮説では、コインが\(p\)の確率ででる、としていますが、この\(p\)の値は0から1まで、無限の候補があります。ではそれぞれの候補が真である確率はどう考えるべきでしょうか。例えば、\(p=0.5\)である確率や\(p=1.0\)である確率はどのように与えられるのでしょうか。このことを考えることが、Bayesianの必須のステップです。このコイントスが友人の間で行われたものではなく、例えば赤の他人との勝負だったとします。相手がどんな人間なのか全く情報のない中で仕組まれたゲームだったとすると、相手がイカサマコインを使うのか、使わないのかわかりません。仮にイカサマコインを使うにしても、どの程度の確率で表が出るコインなのかもわかりません。そうすると、ある\(p\)の値が真である確率はどれも一様だと考えるのが自然であり、ここでは\(P(p) = q\) (\(q\)は定数)と置いておきます。
次に、\(P(D|H, I)\)は、ある\(p\)の値が真である確率はどれも一様だという前提の下で、ある\(p\)が選ばれたとき、表が20回中15回出る確率のことなので
$$P(D|H, I) = \frac{20!}{15!5!}p^{15}(1-p)^{5}$$
と書けます。
分母に現れる\(P(D|I)\)というのは、考えられる全ての仮説でデータを再現する確率を足し合わせたものだから
$$P(D|I) = \int_{0}^{1} dp P(p)\frac{20!}{15!5!}p^{15}(1-p)^{5}$$
と書けます。今、\(P(p) = q\)と置いているので積分の外に出してよく、結局ベイズの定理の式は
$$P(H|D, I) = \frac{q\times\frac{20!}{15!5!}p^{15}(1-p)^{5}}{q\times\int_{0}^{1} dp \frac{20!}{15!5!}p^{15}(1-p)^{5}}$$
と書けます。このように\(q\)が約分できることから、最初に\(q\)とおくのではなく\(P(p) = 1\)と仮定しておいてもよいです。これはどのような前提知識を仮定しても成り立つことであり、仮説の中の一つが成り立つ確率を1と定めても良いと一般化できます。これが許されるのは、分母に\(P(D|I)\)が入っているためです。\(P(D|I)\)というのは、「考えられる全ての仮説でデータを再現する確率を足したもの」であり分母の\(P(H|I)\times P(D|H, I)\)というのは「ある一つの仮説(\(p\)の値を一つに限定)でデータを再現する確率」を表したものです。したがって、ある一つの仮説が成り立つ確率を定数倍しても、分母にも同じように反映されるので約分ができ、最終結果は等しくなります。このような役割を果たすことから、分母は「規格化」と呼ばれます。今後は、ある一つの仮説が成り立つ確率を\(q\)ではなく、”1″として定式化を行います。
ところで、ベイズの定理を書き換えた式を見ると、分母は定数の値になることに気づきましたか。\(p\)が変数になっているように見えますが、積分されてしまうので、結局\(p\)は残りません。すると、分母はただの数になることがわかります。よって
$$P(H|D, I) \propto \frac{20!}{15!5!}p^{15}(1-p)^{5} $$
と書けます。これは\(p\)だけに依存するグラフで、そのコインが確率\(p\)で表が出るコインである確率を表したものです。
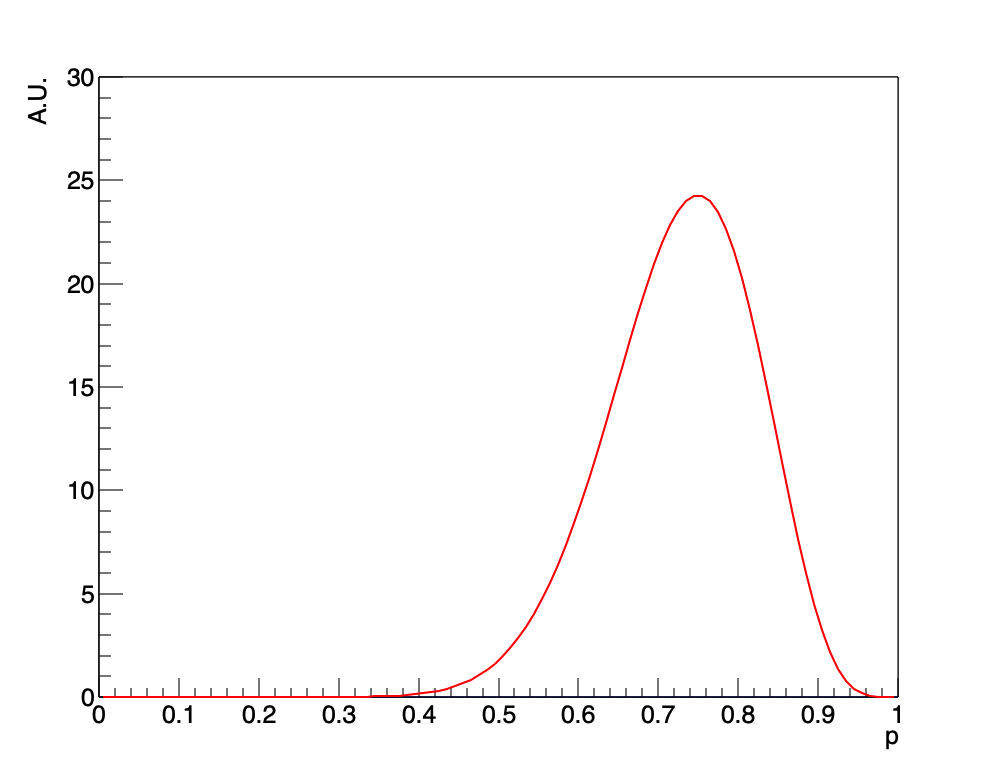
縦軸の絶対値には特に意味はありませんが、グラフから表が出る確率は0.75になる場合がもっとも大きいということがわかります。今、グラフの全区間を積分すると、およそ5.71程度の値になっています。このとき、グラフにおいて、例えば\(p\)が0.6から1.0までの区間を積分したものを考えてみます。この区間での積分値は、5.17程度であり全体のおよそ90%を示していることになります。この90%は何を意味しているのでしょうか。
このグラフは\(P(H|D, I)\)、つまり現在の前提知識と得られたデータの下で仮説(表が\(p\)という確率で出る)が真である確率を表しています。\(p\)が0.6から1.0までの区間を積分したものの絶対値には意味はありませんが、それの全体に対する割合は、あらゆる仮説のうちで、\(p\)が0.6から1.0までの間である仮説が真である確率を意味していることになります。すなわち、そのコインについて、表が60%以上の割合で出るコインである確率が90%である、という解釈ができます。そのようなイカサマコインである確率が90%だということを主張しているわけです。
これがベイジアン的な解釈です。すなわち、20回中15回表が出た。それは、そのコインが表が60%以上の割合で出るコインである確率が90%だったことを意味している。ゆえに、お前はイカサマコインを使ったのだ! という風に考えることができるわけです。
ベイジアンの解析において、重要な点は最終結果が「前提知識」の決め方に左右されるということです。今の場合、相手に何の情報もなく、どのようなイカサマコインが使われるかに関して一様分布を仮定していました。しかし、もし相手が信頼できる友達で、その友達がコイントス勝負を持ちかけてきた時に、同じように20回のコイントスで15回表が出たという場合には、前提知識の部分を変更するべきでしょう。例えば、99.9%の確率で友達は正当なコインを使い、0.1%の確率で友達がイカサマコインを使うような場合を考えてみます。正当なコインと言えど、表・裏が出る確率が完全に0.5であることは保証できないので、多少のずれを許しておきたいものです。そこで、先ほど紹介した正規分布を使って、そのずれを表現します。すなわち、正当なコインにおいて表が出る確率を横軸にした分布が、平均が0.5で幅が0.01程度の正規分布に従うと仮定します。
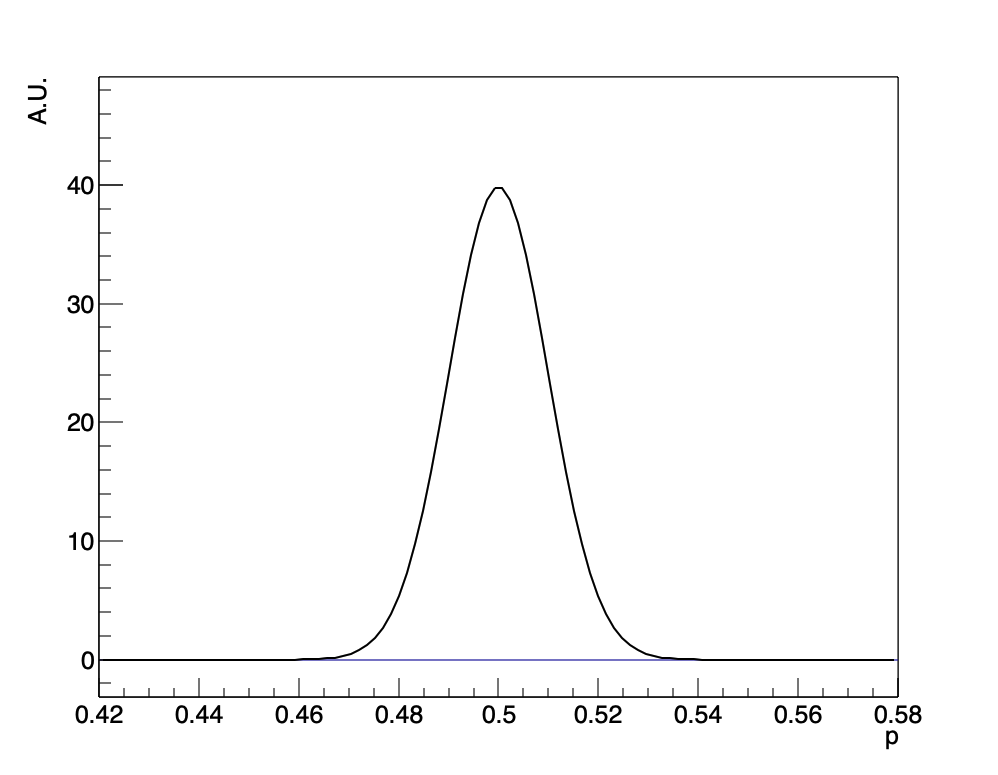
このグラフが平均0.5で幅が0.01の正規分布です。表が出る確率はほとんど46%から54%の間にあることがわかりますね。イカサマコインの方は、確率\(p\)に関しては先ほどと同じように\(p\)に関して一様な分布であると仮定します。すると\(P(H|I)\)というのは今度の場合は
$$P(H|I) = 0.999\times \frac{1}{\sqrt{2\pi}\times0.01}\exp\left({-\frac{(p-0.05)^{2}}{2\sigma^{2}}}\right)+0.001\times1$$
と変更されます。そうするとこの式は定数ではないので、\(P(H|D, I)\)もこれに応じて変更されるので、
$$P(H|D,I) \propto \frac{20!}{15!5!}p^{15}(1-p)^{5} \times P(H|I)$$
と書かれることになります。ベイズの定理の分母は結局\(p\)の積分なので、定数になります。ゆえに形だけを議論したいのであれば、分母は無視して大丈夫です。上の式も少しややこしいですが\(p\)のみの関数なので、グラフに書くことができます。
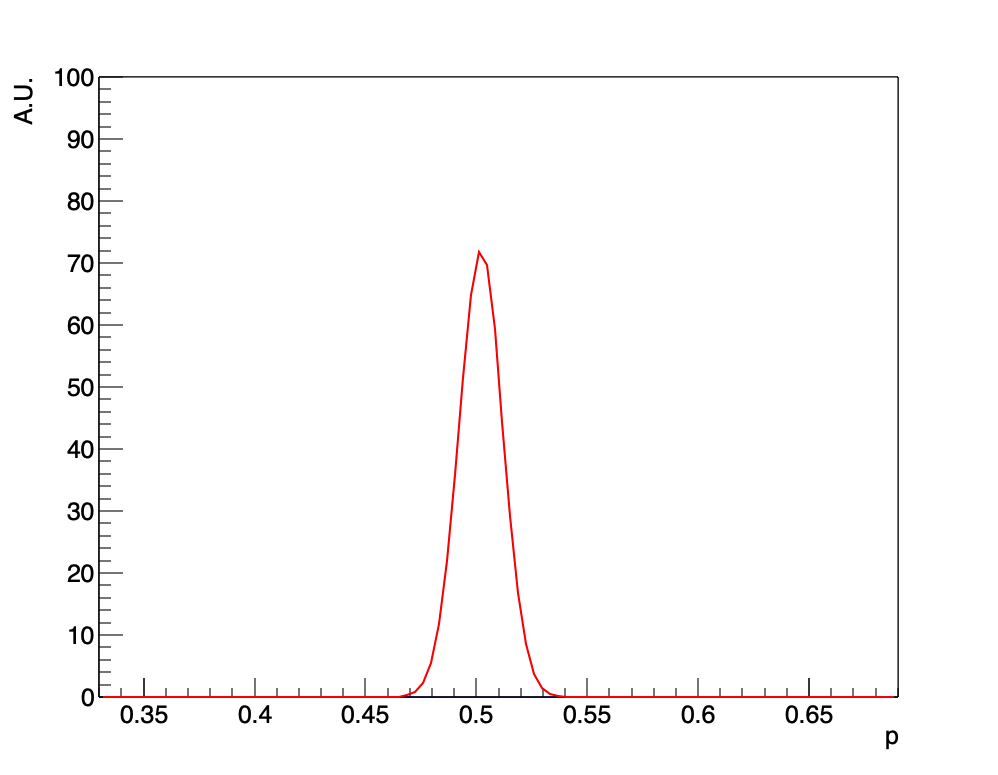
これが今の前提知識を使った場合のグラフです。同じデータ(20回のコイントスをして15回表がでる)にも関わらず、全く異なる結果が出てきました。今回も先ほどと同様に\(p\)が0.6以上の場合の区間を積分した面積の、全体に対する割合を計算するとわずか0.3%程度です。すなわち、20回のコイントスをして15回表がでたが、にも関わらず友人がイカサマコインを使っている確率はわずか0.3%程度だったという結論になります。このように、前提知識に応じて最終結果が劇的に変わるので、どのような前提知識を使うのがもっとも合理的であるかを適切に選ぶことがベイジアンの解析では重要なのです。ちなみに、上のグラフで\(p=0.75\)付近を拡大してみると
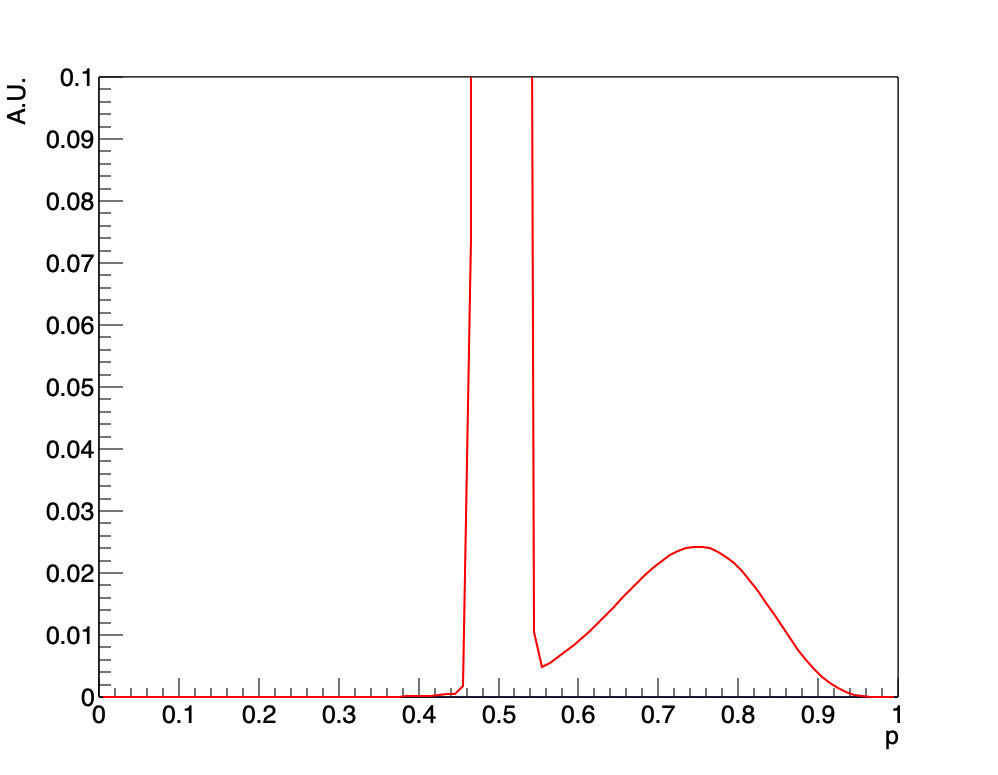
確かに小さいピークが立っているのが見えます。これはデータがより極端に偏れば偏るほど大きなピークとなっていきます。
ベイジアンの解析は、ある「仮説」の妥当性・信頼性を図るのに非常に適しています。コイントスの最初の例では、「相手が正当なコインを使った」という仮説は90%の確率で棄却される(統計学では仮説が偽である場合、仮説が棄却される、という)ことがわかります。逆に、後半の例では「相手が正当なコインを使った」という仮説は十分に信頼に足る事実だということがわかります。研究では、「データ」を用いてある仮説を検証するということが、文系・理系双方にとって重要です。仮説検定と呼んだりしますが、ベイジアンの解析は仮説検定をするときの重要な手段の1つとなるわけです。
逆境無頼カイジに登場する「地下チンチロ」とは
準備ができたところで、そろそろ本題に入りたいと思います。まず、サイコロ賭博の1種にチンチロというゲームがあります。物語に登場する地下チンチロのルールは以下のように設定されています。
・親(1人)と子(複数可)を決め、親と子同士で出目の強さを競う。
・サイコロは3つ。お椀にサイコロ3つを投げて出たものを出目とする。
・出目の強さは次のように決まる。
・(2つが同じ数字)+(異なる数字)(aab) → 出目は b
数字が大きいほど強い。
・456→シゴロという出目。上の出目のすべてより強い。
・1以外のゾロ目→上のすべての出目より強い。
・111→ピンゾロ。上のすべての出目より強い。
・それ以外→出目はなし。この場合、3回までサイコロを振る権利がある。3回振っても出目がなければ出目なし。
・123→ひふみ。上のすべての出目より弱い。
・ションベン → サイコロがどんぶりから外に出る。上のすべての出目より弱い。
ここで、カイジの敵「大槻」は四五六賽を導入してイカサマを図ります。四五六賽とは四の裏に四、五の裏に五、六の裏に六が書かれたサイコロであり、以下の確率で出目が決まります。
ゾロ目・・・約11%
シゴロ・・・約22%
六の目・・・約22%
五の目・・・約22%
四の目・・・約22%
要はイカサマサイコロです。物語ではカイジは大槻のイカサマサイコロを、四五組(大槻から給料のピンハネを受けた仲間たち)の1人である三好のメモ(自分が参加した全てのチンチロ勝負の出目を記録したメモ)を頼りに突き止め、それを拠り所にして下克上を果たします。
ところで、イカサマサイコロを使われるとどの程度勝率は変わるのでしょうか。出目を見ればわかる通り、四五六賽を使っても確実に勝てる訳ではありません。四五六賽と普通のサイコロを使った時の四五六賽の勝率を、簡単な確率計算で求めてみようと思います。この計算では、双方にションベンはないものと考えます。結果だけ示すと
四五六賽の勝率:\(\frac{4362}{5832} \simeq 0.7479\).
普通の賽の勝率:\(\frac{924}{5832} \simeq 0.1584\).
引き分け:\(\frac{546}{5832} \simeq 0.09362\).
となります。このように、イカサマサイコロを使えば、普通のサイコロに比べて期待値として「圧勝」できることがわかると思います。しかも、必ず勝つ訳でもなく、適度に負けることがあるため、イカサマであることの煙幕にもなるという絶妙のサイコロであるということができます。
地下チンチロ勝負とベイジアン解析
この地下チンチロ勝負を主題として、ベイジアンの解析を試みようと思います。問題設定としては、地下チンチロ勝負で大槻と\(N\)回勝負を行い、大槻側の勝利回数が\(A\)回であった時、大槻が四五六賽を\(n\)回使っていた確率を求めてみます。ここで、大槻が四五六賽を使って勝利した回数を\(a\)回とします。四五六賽を使って勝利する確率を\(q = 0.75\)とし、普通のサイコロを使って勝利する確率を\(p=0.5\)とします。また、大槻が四五六賽を何回使うかどうかに関する情報はない(\(n\)に関する一様分布)と仮定します。ベイズの定理を使うと
$$P(H|D, I) =\frac{P(H|I)P(D|H, I)}{P(D|I)}$$
とかけて、前提知識の部分から\(P(H|I) = 1\)と置くことができます。また、今までと同じように規格化部分は最終的な分布の形に影響を与えないので
$$P(H|D, I) \propto P(D|H, I)$$
と書直せます。そこで\(P(D|H, I)\)を求めれば良いことがわかります。
この式を書き下すためには、大槻が四五六賽を使って勝つ場合と普通のサイコロを使って勝つ場合に分けて考える必要があります。
(1)四五六賽を使って勝つ場合。
問題設定より、四五六賽を使ったのは\(n\)回で、そのうち\(a\)回だけ勝っています。四五六賽を使って勝つ確率は\(q\)なので、\(a\)回勝つ場合は
$$\frac{n!}{(n-a)!a!}q^{a}(1-q)^{n-a}$$
と表せます。
(2)普通のサイコロを使って勝つ場合
普通のサイコロを使うのは\(N-n\)回で、そのうち\(A-a\)回だけ勝ちます。普通のサイコロを使って勝つ確率は\(p\)なので、
$$\frac{(N-n)!}{(A-a)!(N+a-n-A)!}p^{N-n}$$
と表せます。
これを積の形にすると
$$\frac{n!}{(n-a)!a!}q^{a}(1-q)^{n-a}\frac{(N-n)!}{(A-a)!(N+a-n-A)!}p^{N-n}$$
となります。これが四五六賽で\(a\)回勝つ場合に相当します。ところが、四五六賽を\(n\)回使うというイベントにおいて、勝つ回数というのは幾らかの可能性があります。例えば\(N=10\)として、合計で大槻が7回だけ勝つ場合を考えます。四五六賽を4回だけ使う場合を考えると、\(a\)が取りうる値は、1以上4以下です。\(N=10\)なので四五六賽で全敗すると条件を満たさなくなります。よって下限は1で、上限は四五六賽を使用した回数です。また同じ条件で、四五六賽を8回だけ使う場合を考えると、\(a\)が取りうる値は5以上7以下です。下限は先ほどと同じ考えで与えられ、上限は合計の勝つ回数となります。
このように、\(A, n\)の値によって、\(a\)が取りうる値の範囲は変わってきます。下限は、(大槻の合計の勝ち数)と(四五六賽の使用回数)の和が\(N\)を超えなければ\(0\)としてよく、\(N\)を超えるならば超えた分が下限となります。すなわち、
$$\max(0, n+A-10)$$
が下限の値です。次に、上限は、大槻の合計の勝ち数\(A\)が四五六賽を使った回数を超えているならば\(n\), 超えていなければ\(A\)とすれば良いので
$$\max(n, A)$$
が下限の値です。ゆえに求める\(P(D|H, I)\)は
$$P(D|H, I) = \sum_{a=\max(0, n+A-10)}^{\min(n, A)}\frac{n!}{(n-a)!a!}q^{a}(1-q)^{n-a}\frac{(N-n)!}{(A-a)!(N+a-n-A)!}p^{N-n}$$
と書き下せます。複雑な形をしているように見えますが、一つ一つの式はコンビネーション(C)を書き直しただけのものです。この式は、\(N, A\)を定めると\(n\)にのみ依存する式なので、\(n\)に関するグラフを書くことができます。\(N, A\)はデータに相当する部分であり、はじめに10回勝負(\(N=10\))の末、大槻が4回勝った\(A=4\)場合を考えます。この時、\(P(D|H, I)\)は次の形をしています。
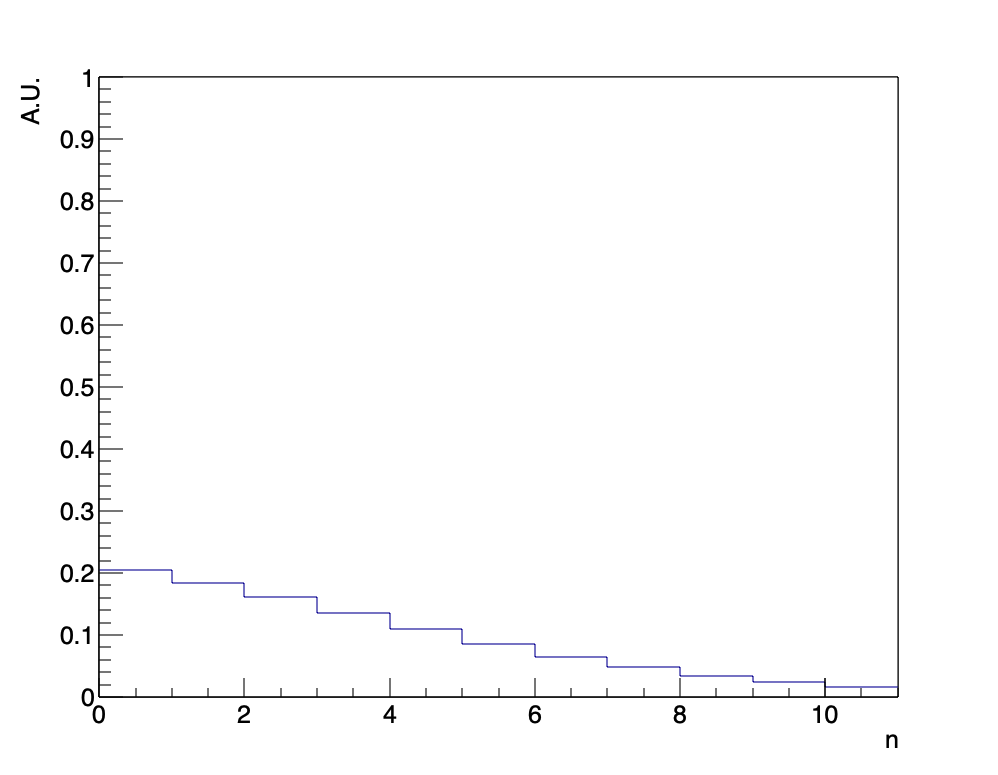
このグラフを使って大槻の勝負を考察すると、大槻が四五六賽を使わなかった確率はおよそ19%程度となります。統計学では一つの基準として5%を下回るとき、その仮説を棄却できるものと考えます。今の場合19%は確かに低いですが、仮説を棄却できるほどには低くないので、大槻が四五六賽を使わなかったという仮説を否定することはできません。
次に、10回勝負(\(N=10\))の末、大槻が8回勝った\(A=8\)場合を考えます。この時、\(P(D|H, I)\)は次の形をしています。
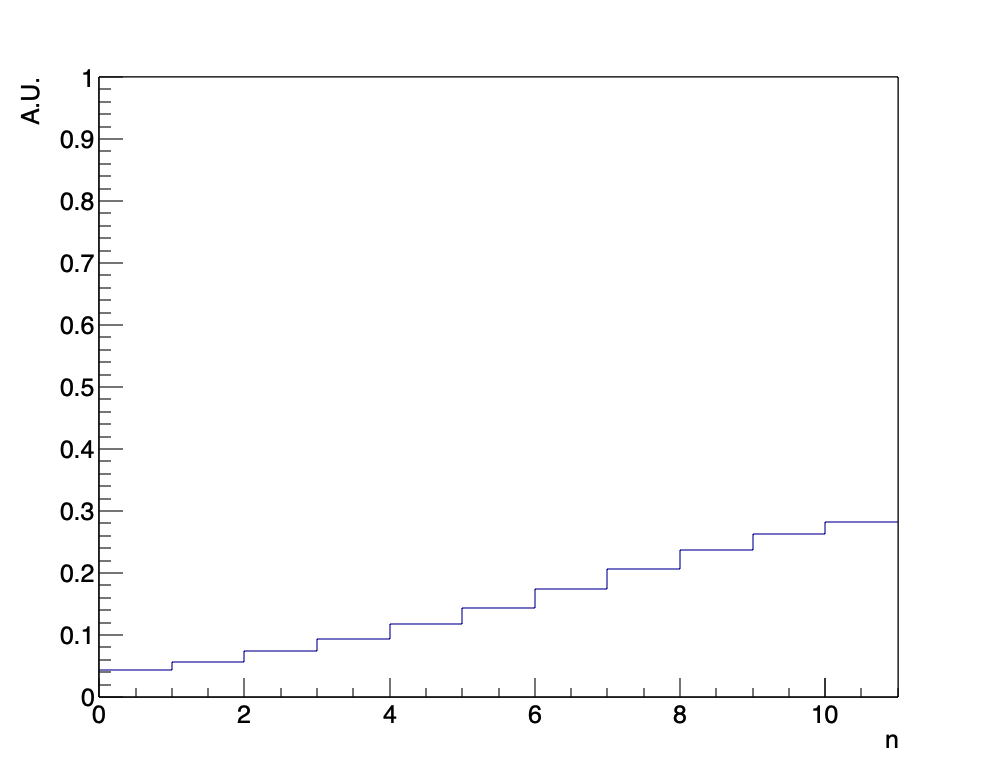
このグラフを使って大槻の勝負を考察すると、大槻が四五六賽を使わなかった確率は3%程度であり、先ほどの基準に照らし合わせると今度は四五六賽を使わなかったという仮説を棄却できることになります。ゆえに、このデータ、前提知識の場合には大槻は四五六賽を1回以上使っていたと見做すことが妥当である、と言えるわけです。
さて、Bayesianの解析では、異なる前提知識を用いて同じデータを解析することが重要でした。勝負の場において、10回中10回とも四五六賽を使うというのは幾ら何でもやりすぎのように思います。せいぜい2~3回程度が普通でしょうか。そこで大槻が四五六賽を振る傾向として次を仮定します。
・10回勝負において四五六賽を5~10回使う確率:それぞれ0.05
・他:0.14
この時の\(P(H|D, I)\)は関数\(f(n)\)を\(n\leq4\)のとき\(f(n)=0.14\), \(n>4\)のとき\(f(n)=0.05\)と定義して
$$P(H|D, I) \propto f(n)\times\sum_{a=\max(0, n+A-10)}^{\min(n, A)}\frac{n!}{(n-a)!a!}q^{a}(1-q)^{n-a}\frac{(N-n)!}{(A-a)!(N+a-n-A)!}p^{N-n}$$
とすれば良いです。先ほど、大槻が四五六賽を使わなかった仮説を棄却できた、10回勝負(\(N=10\))の末、大槻が8回勝った\(A=8\)場合を考えます。
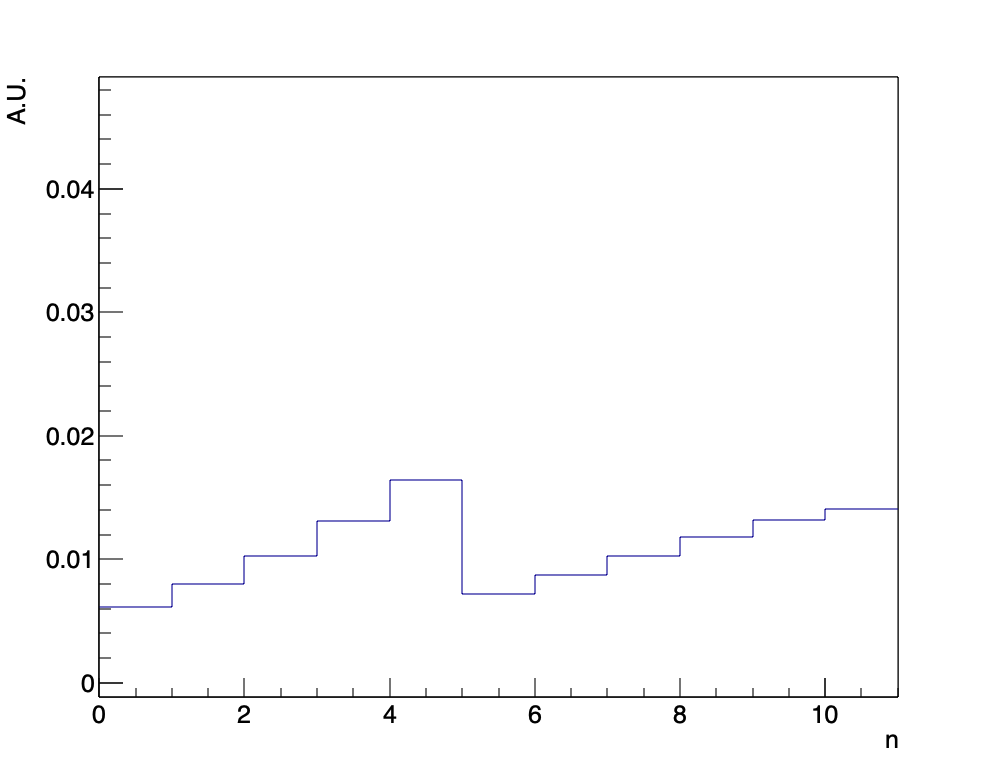
前提知識からわかる通り、大槻が四五六賽を10回使っていた確率よりも4~5回使っていた確率の方が高く出ていますね。このとき、大槻が四五六賽を使わなかった確率を計算してみるとおよそ5.2%であり、ギリギリ先ほどの基準に到達しないことがわかります。ただ、より現実に即した前提知識を仮定しても、かなりの確率で四五六賽を使っていたと推測できることがわかります。他により今の場合にふさわしい前提知識があると思いますので、それらを考察してみるとより面白いかもしれません。
最後に
ここで話したベイジアンの解析は実際に物理研究の場でもよく登場します。特に未発見の物理現象を探索するときには、「今までの物理理論である実験・測定データを説明できる」という仮説を立て、その仮説が真である確率がX%未満であることを示すことで、今までの理論を超えた物理があることを証明します。特にヒッグス粒子のような未知の粒子の存在などでは、ここでのXは5%などではなく、0.0001%を基準にします。その仮説が真である確率が0.0001%未満であれば新たな物理の「発見」とするのが、物理研究の習慣のようです。ここでの簡単な例によって、物理研究の一端をお見せできたのであれば、幸いです。
以上で述べた統計学の基本については、
https://www.phas.ubc.ca/~oser/p509
のサイトを参考にしています。英語のサイト(授業のシラバス)ですが、統計学の基本を学ぶ上で非常に興味深い内容が揃っています。こちらも合わせて紹介させていただきます。

コメント