こんにちは、眠る亀です。
このブログにアクセスして、質問していただける方が現れるまで、こちらから情報発信を続けようと思います。今回は、必要性・十分性に関する自問自答です。
自問
高校数学の途中に現れる、必要条件・十分条件って、結局何? 何に役に立つの?
自答
必要条件と十分条件といえば、「AならばB」という命題があってこれが「真」のとき、
AをBが真であるための十分条件、BをAが真であるための必要条件、という風に教科書では紹介されますね。
で、結局何?
となる人は多いのではないでしょうか。実は、この二つの概念は数学の肝と言っても良いものなのですが、定義がややこしい上に、一度出てくるとそれ以降全く顔を出さないので、その重要性には気づきにくいのです。しかし、大学教授はこの二つの重要性を理解しているので、入試問題ではこれらをベースとした問題を出題してくることになります。すると、定義しか知らない生徒には、「自分の出した答えがなぜ間違っているのか」すらもわからないことがあります。
必要条件と十分条件の違いは、「必要条件はそれが満たされることなしに答えとなることはない」が「十分条件はそれが満たされさえずれば答えとなる」という点でしょうか。必要性と十分性がどのように使われるのかを具体的な場面で考えてみましょう。わかりやすいように、「命題」と「真偽」というのではなく、ある「問題」があってそれに対する「正誤」がある、という関係に置き換えます。
さて、ここに、4人の人間がいます。それぞれの人間は次のような人達です。
A: イケメンで優しい
B: イケメンで冷たい
C: ブサメンで優しい
D: ブサメンで冷たい
問題:この中で結婚しているのは誰でしょう?
これだけ聞いてもとっかかりがありません。そこで、次のような真実がわかったとします。
「結婚している人は優しい」
すると、皆さん、自然にB, Dを候補から外しますよね? なぜといえば、「優しくなければ結婚できないって言ってるじゃん」。皆さんは自然に「優しい」ということが結婚するための「必要条件」だって分かってるってことなんです。
このように「必要条件」が与えられると、答えの候補を絞り込めるんです。これが重要です。
しかし、「優しければ結婚できる」とも言っていないですよね。だから、AとCが共に結婚しているとは限りません。そこで、この二人に聞き込みをしてみます。
私:「結婚していますか?」
A:「はい」
C:「はい」
これで、問題の答えはA, Cとわかりました。実はこの「聞き込み」の部分が「十分性」なんです。「結婚していますか?」に「はい」と答えれば、他の条件など関係なく、もう「結婚している」のは自明ですよね。
すると、皆さんはこういう疑問を持つはず。
じゃあ、最初から聞き込みすりゃいいじゃん。
ごもっともです。しかし、今回は候補が4人だったから良いものの、もし100人、1000人、10000人といたらどうでしょうか。聞き込みなんてやっていられないですよね。まして、数学の問題では、答えの候補が無限ということもよくあります。
そこで、この「必要性」「十分性」の考え方を使います。つまり、「必要性」で答えの候補を絞り込み、「十分性」で答えとなることを確認する、という手法です。「必要条件」「十分条件」は本来、このような数学的な考え方を身につけるための「準備」なのですが、定義を覚えることだけが重要になってしまい、本来の役割が見えにくくなっているのです。
それでは、この概念を具体的な入試問題に適用してみます。
一橋大学 2008年 第1問

さて、「前編」で聞き込みができれば苦労はない、という話をしましたが、今回の問題は解の個数が無限個ですので、聞き込みはできませんね。そこで、「必要性」の出番です。すなわち、問題を解く方針として、5n^2-2kn+1<0を満たす整数nがちょうど1個になるために必要な条件、を探すということです。解の個数を聞かれていますので、この2次不等式を解いてみたくなるのが人情でしょうか。解くと、以下のようになります。
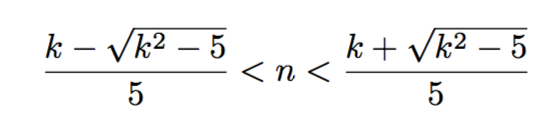
さて、この不等式をぐっと睨みましょう。解の個数を聞かれているので、重要なのはこの解が許される幅です。幅は右辺から左辺を引いたもので、その幅を今、Wと置きましょう。さて、Wの必要条件は何でしょうか。下から攻めましょう。
W=0のとき
これはもう、論外ですね。解があろうはずがありません。
W=1のとき
これは左辺と右辺を上手くとれば、解を1つにすることができます。例えば、左辺が1.5, 右辺が2.5になるようにkを選べれば、整数nの解が一つに定まりますね。しかし、W<=1という範囲は、厳しすぎるのです。
厳しい、というのはどういうことでしょうか。例えば、W=1.5としましょう。この場合でも、例えば左辺が1.2, 右辺が2.7となるようなkが選べれば、問題の条件を満たしています。厳しいというのは、「W<=1の外の範囲でも解となるようなものが存在する」ということです。必要性を考えるときに重要なことがあります。
考えうる中で、ギリギリまで緩い必要条件を求める。
これ、わざわざ大きな文字で言っていますが、人間生活でも当然のように意識していることなんですよ。例えば、警察官が犯罪操作を行っているとき、容疑者を見つけるときには、ゆるい必要条件から考えていって、少しずつ厳しい条件にしていくはずです。数学も同じです。解という名の犯人を捕まえるために、ギリギまで緩いが確実に絞り込める必要条件を探すんです。
W=2のとき
例えば、左辺が1で右辺が3のような場合ですね。この場合も解は1つしかありません。そして、この時が、ギリギリまで緩い条件である、ということに気づきますか? 例えばWが2よりも少し大きくなれば、2個以上の解が発生するようなkが存在しうるんです。仮にW=2.1とすると、左辺が1.95、右辺が3.05のような場合が可能ですが、これでは整数解が2, 3の二つとなってしまいます。
ということは、解の個数が1つということは、右辺から左辺を引いたものが2以下でなければならない、ということなんです。これが、「考えうる中で、ギリギリまで緩い必要条件」です。なぜ、ギリギリでなければならないのでしょうか。「数学的に正しい答えを出す」ということだけを考えるなら、「ギリギリ」である必要はありません。しかし、必要条件をさらに緩くしてしまうと、「十分性」を確認するときに、時間がかかってしまいます。
先ほどの犯人を見つける警察官の例に戻りましょう。「犯人は日本人」であるということを突き詰めたとしても、そこから聞き込みをして犯人を見つけるのは馬鹿げています。「犯人は日本の鳥取県に住んでいて、農業を営む60歳前後の男性であり、175 cm程度の上背である」とまで絞り込めていたら、聞き込みも楽ですよね。
だから、数学的にはここでの必要条件をW<=3などとしても正しい答えは出ます。しかし、最短の手間で答えを出すなら、「W<=2」とするのが賢いということなんです。問題集や洗練されたプロの解説では、ここまでの説明は載っていないで、最短で答えを求める手順しかありませんよね? 素人がブログ等で問題解説をするときは、こういうところを意識して解説してこそ意味があるように思います。
さて、話が逸れましたが、この問題における「ギリギリまで緩い必要条件」はW<=2ですがこれをkの式にすると、以下のようになります。
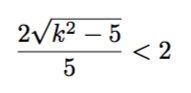
これを解くと、混合の中身が負でないことから、5<k^2<30という式が出てきます。すなわち、kの候補は3, 4, 5の3つです。さて、もう一度確認しますが、ここで使った条件はあくまでも「必要条件」のみですね。すなわち、この3つは解を満たすための「必要条件」でしかないのです。数学の解というのは「必要十分条件」のことですから、まだ足りません。警察官の立場から言うと、容疑者が絞られただけである、と言うことができます。しかし、無限個の可能性から、3つまで絞れたのですから、ここからは胸を張って「聞き込み」をしましょう。数学での「聞き込み」は代入のことです。
最初の2次不等式に戻って、k=3, 4, 5を代入して丁寧に計算してみてください。すると、k=3のときは、問題の条件を満たさないことがわかります(ちなみに、解が0になります)。他の場合は、バッチリ問題の条件を満たすので、解はk=4, 5であると結論できます。
必要性と十分性の考え方がいまいち身についていないと、「必要条件」を出したところで満足してしまうことがあります。しかし、覚えていてください。「必要条件」を出して満足してしまうと、日本の裁判は「冤罪裁判」の嵐になってしまう、と言うことです。皆さんも優秀な警察官となって、数々の解を暴いていってくださることを応援しております。
最後に、このブログを書くベースとなった私のYoutube動画ですが、下記にリンクを張っておきます。ブログの方が詳しく解説していますので、改めて見直すこともないと思いますが、よろしければご覧ください。
本日は最後までご閲覧いただき、ありがとうございます。

コメント
こんにちは。突然すみません。
もし良ければ質問させて欲しいです。
この前同値について調べていたらこちらを見つけて納得できたので自分でもしてみたらよく分からなくなりました。
知恵袋にも投稿したのですが信憑性に欠けるような気がしてこちらで聞いてみようと思い今に至ります。
以下知恵袋と同じ内容です。
y=x^2+aとx^2+y^2=9が接するとき、定数aの値を求めよ。という問題で、先生に質問したときに
“二式から xを消去した方程式の判別式D=0と、円と放物線が接するということは同値ではない”
と言われたのですが、
そうならば、問題集での解答でD=0をなぜ用いているのでしょうか。
自分は、
接するとは共通接線をもつことなので、a=±3がまず考えられ、もうひとつの場合に2点で接するな、と思ったのですが、2点で接することからD=0を使ってしまったら、接する⇨D=0もしくは接する⇔D=0と認めることになるのじゃないかと引っかかるのです。
解答では
“この2次方程式は重解をもつのでD=0でa=-37/4、
このとき2次方程式の解はy=-1/2で-3<y<3を満たす”
とありました。
重解を持つ⇔D=0は言えるのですか?
また、a=-37/4を代入して確認していることから、”この2次方程式は~”は必要条件だったのでしょうか。
もう何がなんだかわかりません。色々なサイトを調べたのですが、自分が解く時にどれが必要条件かをきちんと理解できていないので、教えていただきたいです。
以上です。気分が向かれたらで良いのでよろしければ教えて頂きたいです。
むりなお願い申し訳ないです。
みんみん様、
ご質問ありがとうございます。質問の内容を拝見いたしました。
提示していただいた問題は、同値性をきちんと理解するために非常に重要な問題のように思います。
私なりの見解を週末までに記事にまとめたいと思いますので、よろしければご覧いただけますでしょうか。
よろしくお願いします。
みんみん様、
記事を公開いたしました。
「放物線と円が交わるための条件を同値性をテーマに掘り下げる」という題名です。
もし、ご不明な点があれば、遠慮なくおっしゃっていただければ、対応いたします。
自分の質問に貴重な時間を割いて教えていただきありがとうございます!返信遅くなりすみません。
先生に聞いてもよく分からなかったので諦めていたのですが、質問してよかったです。
最後の微分はまだ分からないので、休みのうちに予習してみます。
何度も申し訳ないのですが質問させてください。以下が質問です。
問題を解いていくときに、今回は放物線と円でしたが、”○○と△△が接する“ という問題が出たら、毎回 ”D=0⇔それらが接する” かどうかを調べるべきですか?
放物線と直線や、円と直線のときは青チャートに接する⇔D=0とあったので、特定の円と直線で記事のように同値であることを示してみようとしたのですが、どうしたらいいのか分からなくてつまづいてしまいました。
また、円と放物線の問題では “接する⇒D=0”
を反例があるから偽とされていましたが、反例に気付いていないときや他の問題ではどうしたらいいのでしょうか。
度重なる質問本当にすみません。
よろしければでいいので教えて頂きたいです。
みんみん様、
いえいえ、疑問があれば遠慮なくどうぞ!
記事をご覧くださり、ありがとうございます。
コメント欄には数式を書く機能が充実していないので、
同じ記事「放物線と円が交わるための条件を同値性をテーマに掘り下げる」
の終わりに、追記として返答いたしました。
円と直線について、接する⇔D=0を示す一例も載せました。
よろしければ、そちらをご参照いただけますでしょうか。
ありがとうございます!
教えていただいたことでやっと同値という考え方の外枠だけでも掴めたと思います!
理解したつもりになっているかも知れないので何度も記事を読ませていただきます。
本当に貴重なお時間を自分の質問返答に割いてくださりありがとうございました!
みんみん様、
少しでも役に立てたのなら幸いです。
必要条件、十分条件に対する意識は学校の授業でどのように教わるかわかりませんが、
教科書を読んだり、問題集を解くだけではなかなか身につかないものです。
ぜひ、ものにしていってください。
また、何かありましたらお気軽にどうぞ。
突然のコメント失礼します。
必要十分に関する質問でよくy=f(x)がx=a で微分可能であるときの定数a,bの値を求めよといったような問題でy=f(x)がx=aで微分可能である⇄f`(a)が存在するが同値であることとy=f(x)がx=a で微分可能である→x=aで連続であることから求めているんですが、2つ目の方はx=aで連続であることが必要条件でしかなくて上の問題のように十分性が確認できず同値でないので条件を絞っただけだと思ったんですけど先生がおっしゃったように数学の解が必要十分であることを満たさないんじゃないのかな?と混乱してます。
まき様、
コメントありがとうございます。
コメントを頂くたびに、自分の中で無意識に行なっていたことを意識的に
考え直すきっかけになり、とてもありがたいことだと感じています。
こちらの質問に対する自分なりの考察を記事にいたします。
投稿したらお知らせいたしますので、ご参照いただけますでしょうか。
よろしくお願いします。
返信ありがとうございます。ぜひよろしくお願いします。
まき様、
記事タイトル”高校数学における、2つの関数の連結点に関する、微分可能性の議論”
にて、今回の質問に対する考察を載せました。
質問内容から、2つの関数の連結点に関する、微分可能性を証明する問題が
ターゲットかなと思いましたが、もし、違う問題をイメージしていたら修正・加筆いたします。
よろしくお願いします。
とても分かり易かったです。連続性が解答のための必要条件ではなく微分可能であるための必要条件でありさらに微分可能であることから必要条件を出して求めていたんですね。ありがとうございました!!!
すみませんさっきの問題の質問で、必要十分条件になるのは、その求めたa,bの値を代入した上で成り立つからそう言えるのか、それとも微分可能と連続であることでa,bを求める事が同値なんですか?
まき様、
a=2, b=1が解答になるための必要十分条件になる理由に関する疑問ということでよろしいでしょうか。
「関数f(x)が連続である条件の下で、f(x)のx=1における微分係数の値が左側極限と右側極限で一致する」
ことが関数f(x)が微分可能になるための必要十分条件となります。
もっと正確にいうならば、問題例の場合では、関数f(x)がx=1で連続であることは、f(x)のx=1における右側極限が
存在するための必要条件でした。ですので、解答のセオリーとしては、
1. 関数f(x)がx=1で連続であることを要求する。
→ f(x)のx=1における右側極限が存在するようになる(左側極限はもともと存在)。
2. f(x)のx=1における微分係数の値が左側極限と右側極限で一致することを要求する。
↔︎ 関数f(x)がx=1で微分可能となる。
となっているので、1と2を同時に満たすa, bの値がそのまま解答になるための必要十分条件であると言えます。
すなわち、まき様の言葉で言うと、
>必要十分条件になるのは、その求めたa,bの値を代入した上で成り立つからそう言える
訳ではなく、
>微分可能と連続であることでa,bを求めること
この微分可能という表現を、「f(x)のx=1における微分係数の値が左側極限と右側極限で一致すること」
に言い換えれば、その通りだと言えると思います。
なるほど!!めちゃくちゃスッキリしました。質問に質問を重ねてすみませんでした笑
実はここのサイトで必要十分について理解が深まって数学のモチベが上がりました。本当にありがとうございました!!また参考にさせてください!!
まき様、
数学の理解に少しでも貢献できたのなら嬉しいです!
必要十分性はいつも意識しておかないといけないことですが、
つい答えを求めることだけに集中してしまって、なおざりにしてしまいやすいですよね。
また何かありましたら、お気軽にどうぞ!