放物線と直線に囲まれた部分の面積の最小値

こんにちは、眠る亀です。
知恵袋にて、質問のあった数学の問題について回答します。間違えていれば訂正します。2変数関数の微分は高校の範囲でも扱えると思うので、その解法を選びました。

質問

回答

直線と放物線で囲まれる部分の面積を求めるときには、有名な公式がありますので、それを利用する手段を考えます。放物線(y=ax^2+bx+c)と直線(y=dx+e)の交点のx座標をα、βとするとこの放物線と直線で囲まれる部分の面積は、以下で表せます。

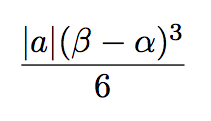
この公式の利用を考えます。よくある手法なのですが、この手の求積問題は次のように求めるのが良いです。といっても、直線の方程式によって多少図が変わります。直線lの方程式をy=ax+bとして、次のように場合分けます。

（I） a>0, b>0
（II）a>0, b<0
（Ⅲ）a<0, b>0

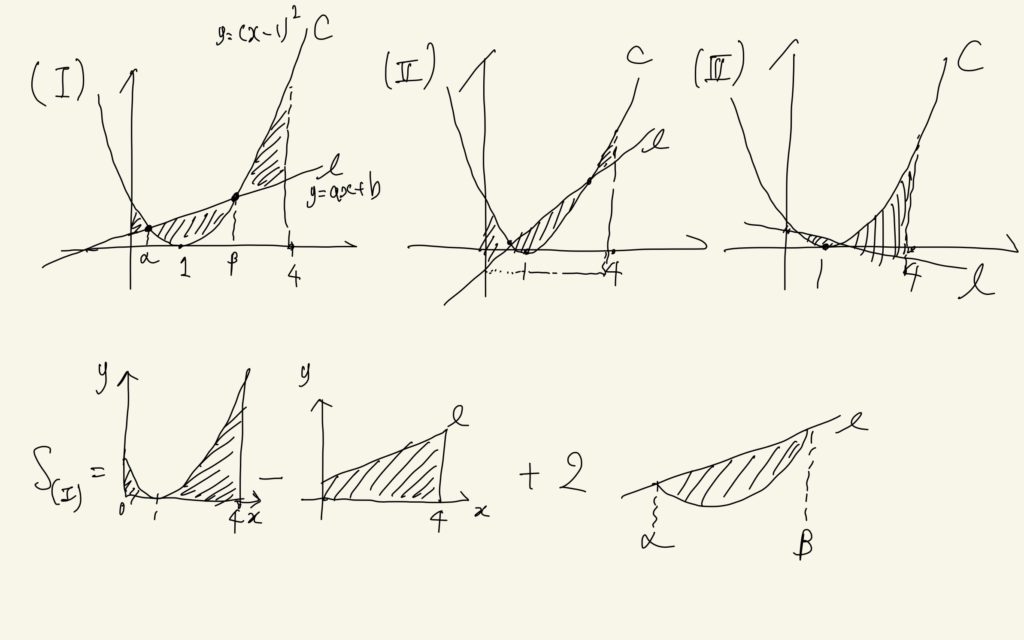
上の図では、（I）の場合の面積を求めています。放物線とx軸で囲まれる部分の面積から、直線とx軸、y軸、x=4で囲まれる部分の面積を引き、放物線と直線で囲まれる部分の面積の2倍を足せば求められます。この通りに計算すると面積の和Sは以下のようになります。ただし、直線と放物線の交点のx座標をα、β(α<β)とします。

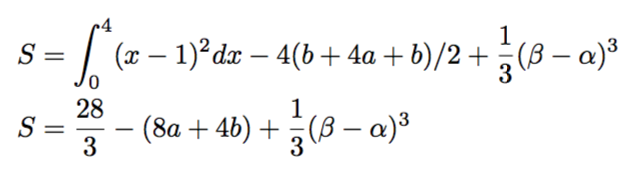
他のパターンでも同じ式になります。

α、βは、放物線と直線の交点のx座標であるから、x^2-(2+a)x+1-b=0と解と係数の関係を用いると、α+β＝2+a, αβ=1-bが成り立つ。これを用いると、β-αは次のように求まる。

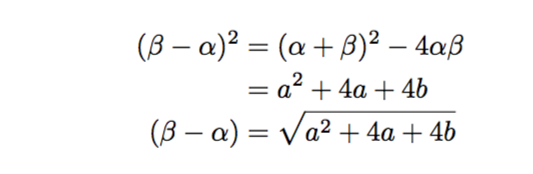
これを用いると求める面積は

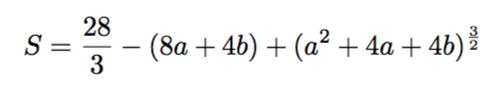
です。a, bについての条件は、放物線と直線が異なる2交点をもつことから、x^2-(2+a)x+(1-b)=0の判別式をDとして、D>0を課すと

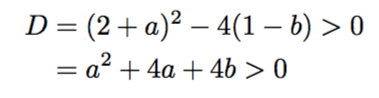
となります。さて、このSですが、まずbの関数だと考えて最小値を求めます。以下のように計算します。

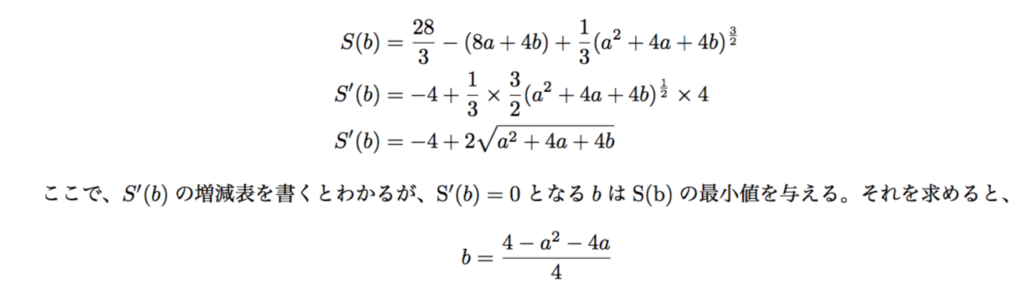
このbの値を、Sに代入すると今度はSはaの関数とみなせる。

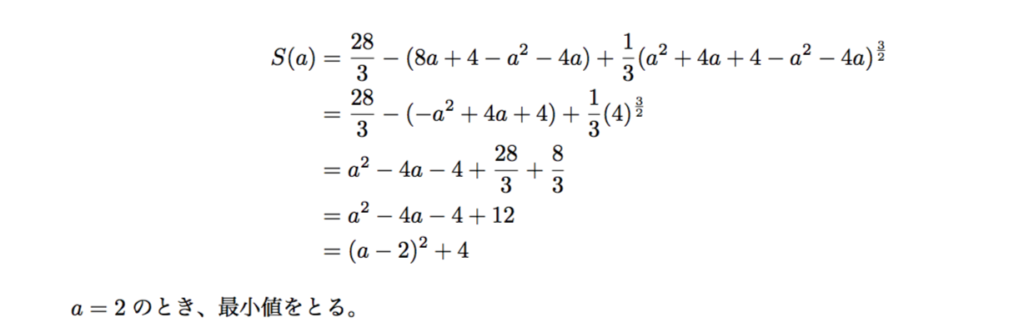
すると、先ほどのbの式から、b=-2とわかる。以上より、求める直線の方程式は

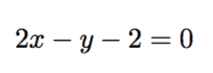
また、ここで求めたa, bの値は、判別式D>0を満たす。

どうでしょうか。