眠る亀です。本日もよろしくお願いいたします。休日は色々な仕事が捗っていいものです(ブラック魂)。その合間に質問にも回答していきたいと思います。
質問
数学についての質問です。(2)についてご解説お願いします…考え方がわかりません…
底面の半径が10の円柱状の容器に水が入っている。水がこぼれはじめるギリギリまで容器を傾けたところ、容器の中心軸は鉛直方向に対し60°傾き、水面は底面の中心を通った。
(1)容器の高さを求めよ。
(2)傾けた状態での水面の面積を求めよ。
(3)水の量を求めよ。
回答
まず、すべての問題を解いてみた感想ですが、立体図形の求積の基礎を学ぶ上で良い問題であると思います。この考え方を身につければ、様々な問題に対応できるようになると思います。質問は(2)に限定されていますが、一応(1)から(3)まで解いてみます。
(1)
とりあえず、よほどの天才でもなければ問題文の言う通りに絵を書いてみると良いです。僕は全く絵心がありませんが、iPadの機能を駆使して書いてみました。数学の問題を解く上ではポイントを押さえていれば、前衛的であっても大丈夫です。
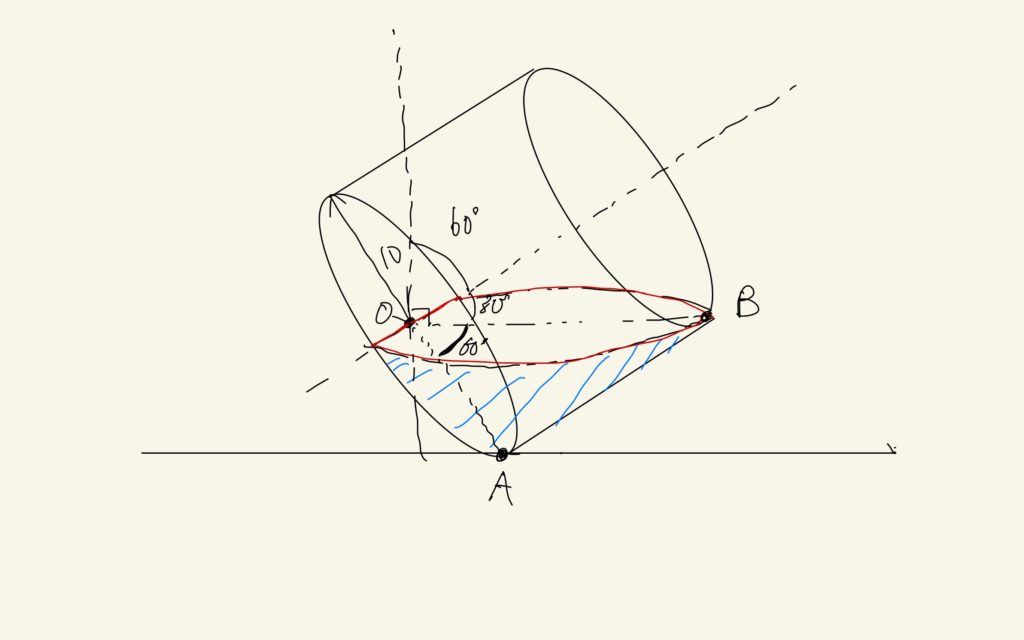
今回のポイントは、「水がこぼれるギリギリで水面が底面の中心を通った」ということを物理的に忠実に再現できるか、ということです。水がこぼれるギリギリということは水面が床に対して平行になるときです。すなわち、その時に円柱の軸が鉛直の線に対して60°傾いたということは、上の図のように、水面と底面のなす角は同様に60°であるということです。なぜなら、上の図のOBと鉛直線が垂直だからです。これがわかれば(1)は解けて
$$10\sqrt{3}$$
です。ちなみに、あとで使うのでOBの長さを求めると、三角定規の比の性質から20です。
(2)
この水面の形がなんなのか、よくわかりません。楕円のようですが、そうでもないような、感じです。ですので、上の図をただ睨んでいても何もわかりません。そこで、「平面図形の面積は微小面積の和である」という考え方を使います。次の図をご覧ください。
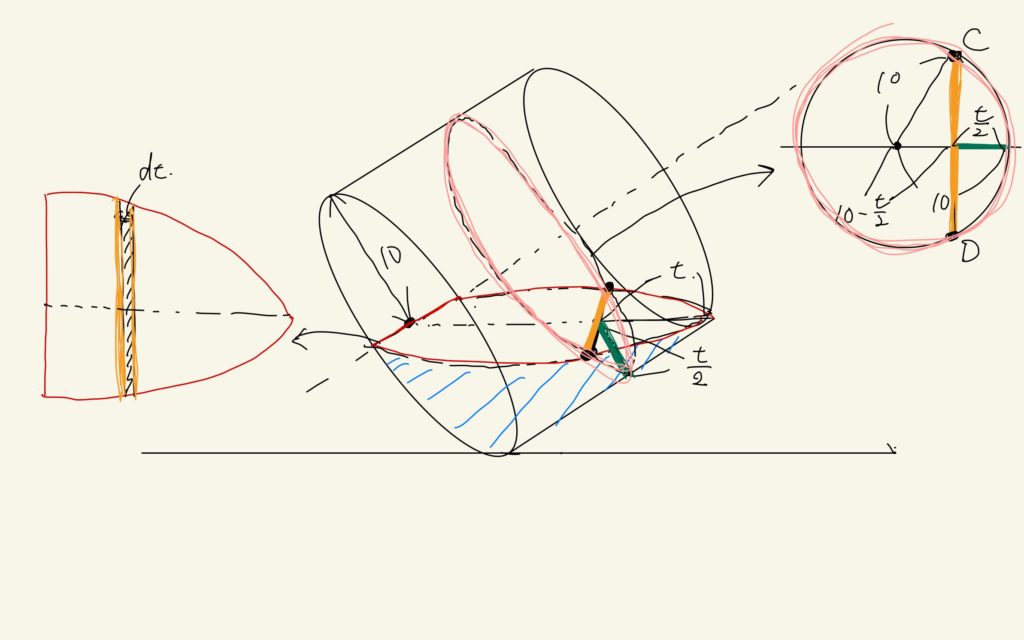
とりあえず、色々、色をつけてみました。水面は赤、水は青、円柱の底面と平行に切断した断面をピンク、そしてピンクの断面と水面の交点を結ぶ線分をオレンジ、オレンジの直線と容器との距離を緑で表しています。まず、左の図について、説明します。
赤で囲った面積を求めることが目標です。これは、図形の中心軸(点線)に対して垂直にdtの幅で切り取った微小図形の面積の和で求められます。例えば、図形の中心軸にそって長さtの位置にあるオレンジの線分の長さをL(t), 中心軸上の図形の長さをTとすれば求める面積Sは
$$S = \int_{0}^{T}L(t)dt$$
と書けます。L(t)dtが微小面積ですね。今、Tは20ですので、Sを求めるにはオレンジの長さL(t)を求めれば良いです。これを求めるために、右の図を用います。真ん中の図で、tのところでこの円柱を底面に平行に切断するとピンクの断面が得られます。これは当然円です。また、緑の線の長さはやはり三角定規の性質からt/2とわかります。ここで右の図に移ります。
緑の長さがt/2, 半径が10の円とわかっているのでオレンジの長さは三平方の定理から
$$L(t) = 2\times \sqrt{10^{2}-\left(10-\frac{t}{2}\right)^{2}} = 2\times\frac{1}{2}\sqrt{t(40-t)} = \sqrt{t(40-t)}$$
です。さて、これでお膳立ては整いました。あとは積分の計算をします。
$$S = \int_{0}^{20}\sqrt{t(40-t)}dt$$
で、これどう解くの? ってことなんですが、経験を積むとsinかcosで置換をするとうまくいきそうなことがわかるようになります。ここではsinの方を使いましょう。経験と言いましたが、とりあえず、置換のコツはいかにして邪魔ものを消すかということです。
“ここでの計算を妨げているのは根号なので、これを消しにいく。混合を消すためには中身を2乗にしないといけない。ここで根号の中身から1-(cosθ)^2 = (sinθ)^2の形が見えてくる。よし、sinで置き換えよう。”
$$t = 40\sin^{2}\theta$$
と置換します。置換に付随する手続きとして以下のことをします。
$$t = 0 \to \theta = 0, t=20\to\theta = \frac{\pi}{4}$$
$$\frac{dt}{d\theta} = 80\sin{\theta}\cos{\theta}$$
これで積分式を置き換えます。
$$S = \int_{0}^{\frac{\pi}{4}}\sqrt{40\sin^{2}{\theta}\cdot40(1-\sin^{2}{\theta})}\cdot80\sin{\theta}\cos{\theta}d\theta$$
$$S = \int_{0}^{\frac{\pi}{4}} 40\cdot80\cdot\sin^{2}{\theta}\cos^{2}{\theta}d\theta$$
$$S = \int_{0}^{\frac{\pi}{4}} 3200\cdot\frac{1}{4}\sin^{2}{2\theta}d\theta = 800\int_{0}^{\frac{\pi}{4}}\sin^{2}{2\theta}d\theta$$
最後の変形は2倍角の公式
$$\sin{2\theta} = 2\sin{\theta}\cos{\theta}$$
を用いています。ここまでくればあと一歩です。
$$\cos{4\theta} = 1-2\sin^{2}{2\theta}$$
を用いると
$$S = 400\int_{0}^{\frac{\pi}{4}} (1-\cos{4\theta})d\theta$$
$$S = 400\left[ \theta – \frac{\sin{4\theta}}{4} \right]_{0}^{\frac{\pi}{4}}$$
$$S = 100\pi$$
どうでしょうか。
(3)
ここまでやったら最後までやってしまいましょう。体積の場合は次の図を使います。
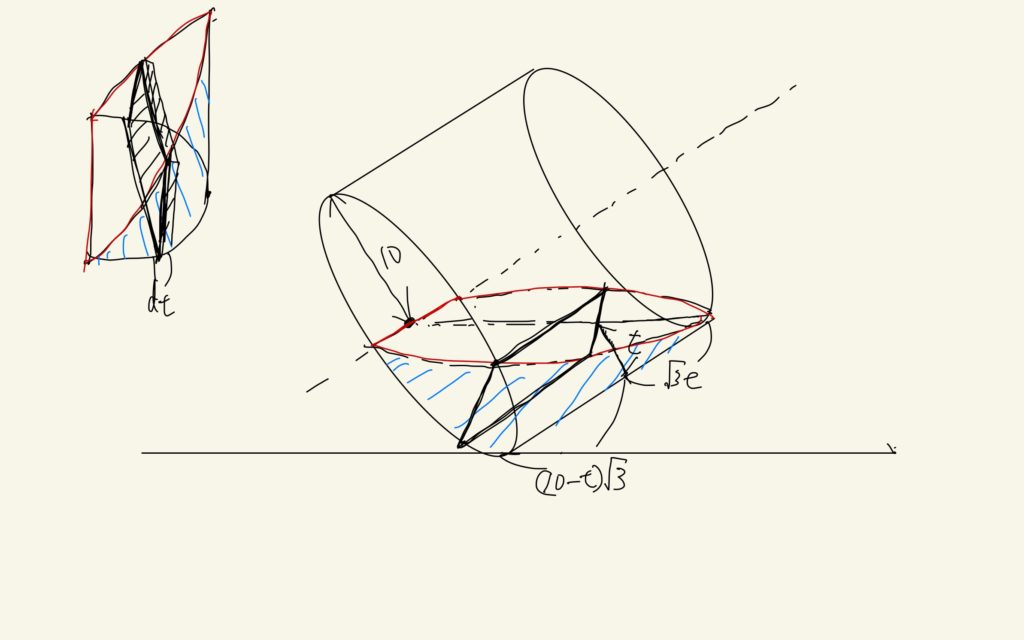
左の図が求める立体図形です。この体積は、この図形の底面に対して垂直に切断してできる長方形を、dtの幅だけずらしてできる直方体の微小体積の和として計算できます。今までの議論から、必要なものはほとんど求められています。例えば、上図のように円柱容器から長方形までの長さをtとします。(2)でオレンジの線分に対応するものを求めると、2√t(20-t)です。三角定規の関係式と(1)から長方形の高さは(10-t)√3です。また、このtは0から10まで動きます。これで準備万端です。求める体積をVとすると
$$V = \int_{0}^{10}\sqrt{3}\cdot(10-t)\cdot2\sqrt{t(20-t)}dt$$
です。置換は定数を少しいじって
$$t = 20\sin^{2}{\theta}$$
とします。dt, dθの関係は
$$\frac{dt}{d\theta} = 40\sin{\theta}\cos{\theta}$$
$$V = 2\sqrt{3}\int_{0}^{10} 10(1-2\sin^{2}{\theta})\sqrt{20\sin^{2}{\theta}\cdot20\cdot(1-\sin^{2}{\theta})}40\sin{\theta}\cos{\theta}d\theta$$
$$V = 16000\sqrt{3}\int_{0}^{10}(1-2\sin^{2}{\theta})\cdot\frac{1}{4}\sin^{2}{2\theta}d\theta$$
ここで2倍角の公式を用いると
$$1-2\sin^{2}{\theta} = \cos{2\theta}$$
であるから
$$V = 4000\sqrt{3}\int_{0}^{10}\cos{2\theta}\sin^{2}{2\theta}d\theta$$
面積と比べて、かなりの親切設計となっています。ゴールはすぐそこです。
$$V=4000\sqrt{3}\int_{0}^{10}\left(\frac{1}{6}\sin^{3}{2\theta}\right)^{\prime}d\theta$$
このように
$$\frac{1}{6}\sin^{3}{2\theta}$$
の微分が
$$\cos{2\theta}\sin^{2}{2\theta}$$
になっていることを見抜きたいです。続けます。
$$V = \frac{2000}{3}\sqrt{3} [\sin^{3}{2\theta}]_{0}^{\frac{\pi}{4}} = \frac{2000}{3}\sqrt{3}$$
いかがでしょうか。

コメント