等面四面体に内接する球の半径

こんにちは、眠る亀と申します。
（エジソンが語った本来の意味合いで）世の中は99%の凡人と1%の天才だなぁ。

本日は、難関大学でさりげなく出てくる等面四面体を勉強してみようと思います。

自問

任意の鋭角三角形△ABC(各辺をa, b, cとする)を用いた、等面四面体に内接する球の半径rはいくらか。

自答

等面四面体でググれば、先頭ページに十分なソースがあります。等面四面体の定義や、その体積など、それで十分学べます。ここでは、その四面体に内接する球の半径に関する公式を作ってみようと思います。一応、等面四面体の定義です。

合同な4つの鋭角三角形を各面とする四面体を等面四面体という。

等面四面体の重要な性質として、いかなる等面四面体でも適切な直方体を作れば、その直方体から切り出せる、というものがあります。以下の図で説明します。

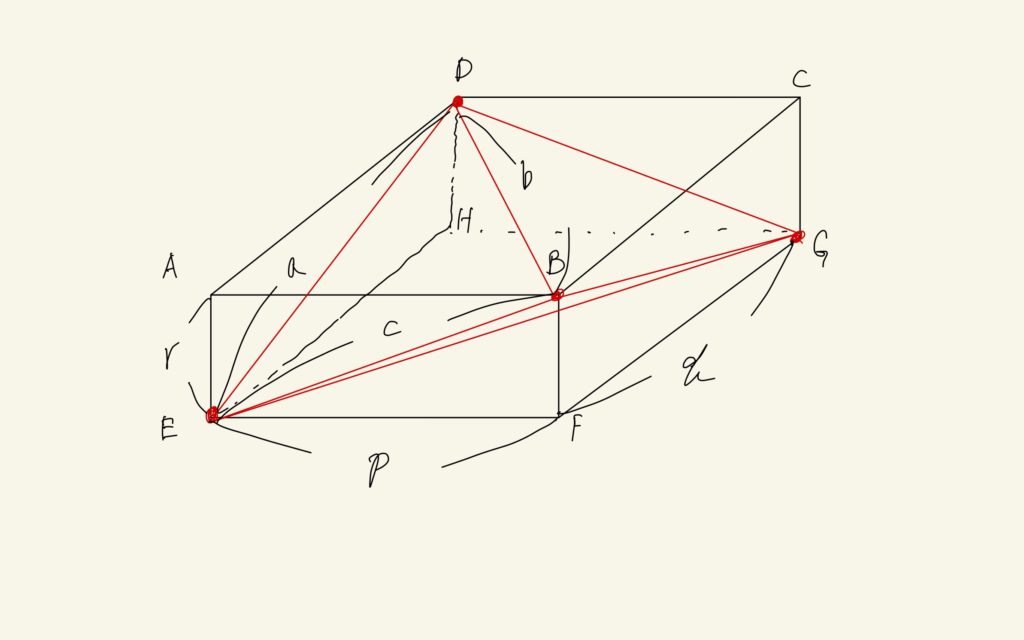
直方体ABCD-EFGHがあり、ここから4点(BDEG)を選んでそれらを結ぶとこの四面体は等面四面体になっています。直方体の各辺をp, q, rとして等面四面体の一つの面の三角形の各辺をa, b, cとすると、以下の式が成り立ちます。

$$a^{2} = r^{2}+q^{2},\ b^{2} = p^{2}+q^{2},\ c^{2} = p^{2}+r^{2}$$

ここで、p, q, rをa, b, cを用いて表します。

$$p^{2}+q^{2}+r^{2} = \frac{a^{2}+b^{2}+c^{2}}{2}$$

$$p^{2} = \frac{-a^{2}+b^{2}+c^{2}}{2}, q^{2} = \frac{a^{2}+b^{2}-c^{2}}{2}, r^{2} = \frac{a^{2}-b^{2}+c^{2}}{2}$$

です。ところで体積Vの等面四面体に内接する球の半径をr、等面四面体の一つの面の三角形の面積をSとすると

$$V = \frac{4}{3}rS$$

という有名な公式があります。ゆえに、ここではV, Sを求めれば良いです。等面四面体の体積は上の図から、直方体から4つの三角錐の体積を引けば良いので

$$V = pqr – \frac{4}{6}pqr = \frac{1}{3}pqr$$

です。p, q, rはすでにa, b, cを用いて表すことができています。

最後に三角形ABCの面積ですが、3辺がわかっているのでヘロンの公式で良いでしょう。

$$S = \sqrt{s(s-a)(s-b)(s-c)},\ \left(s = \frac{a+b+c}{2}\right)$$

以上のことから内接球の半径rは

$$r = \frac{3}{4}\times\frac{1}{3}\frac{pqr}{\sqrt{s(s-a)(s-b)(s-c)}}$$

s, p, q, rをそれぞれa, b, cを用いて表します。

$$r = \frac{1}{2\sqrt{2}}\sqrt{\frac{(a^{2}+b^{2}-c^{2})(a^{2}-b^{2}+c^{2})(-a^{2}+b^{2}+c^{2})}{(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}$$

意外と綺麗な形をしていますね。

最後までご覧いただきありがとうございます。