こんにちは、眠る亀です。最近、物理の研究をしていますが、シミュレーションをするばかりで頭が硬くなっているのを実感します。中学・高校数学の問題は非常に良い、頭の体操になります。
質問
aを定数とする。3次関数f(x) = x^3+ax+a+5はx=1で極小となる。
(1)aの値を求めよ。また、f(x)の極小値を求めよ。
(2)0<t<1とし、曲線C:y=f(x)上の点(t, f(t))におけるCの接線をl:y=g(x)とする。連立不等式
$$y\leq f(x),\ y\geq g(x),\ x\leq2$$
で表される領域をDとし、Dの面積をS(t)とする。S(t)をtを用いて表せ。
(3)(2)のS(t)が最小となるtの値を求めよ。また。このとき、Dのうちx≧0を満たす部分の面積をS1, x≦0を満たす部分の面積をS2とする。S1:S2をもっとも簡単な整数比で表せ。
回答
なんていうか、ドロドロした気配を感じます。とにかく、一生懸命計算していきます。
(1)
関数y=f(x)が極小となるxの値は、f'(x)=0の解です。そこで、f'(x)を求めそこにx=1を代入すると0になるという条件からaを求めることができます。
$$f'(x) = 3x^{2}+a,\ f'(1) = 3+a = 0 \leftrightarrow a=-3$$
よって、f(x) = x^3-3x+2と決まりました。x=1のとき極小となると述べていますので、極小値はここにx=1を代入すれば良いです。ゆえに、極小値はf(1) = 0です。
(2)
領域Dを図示してみます。
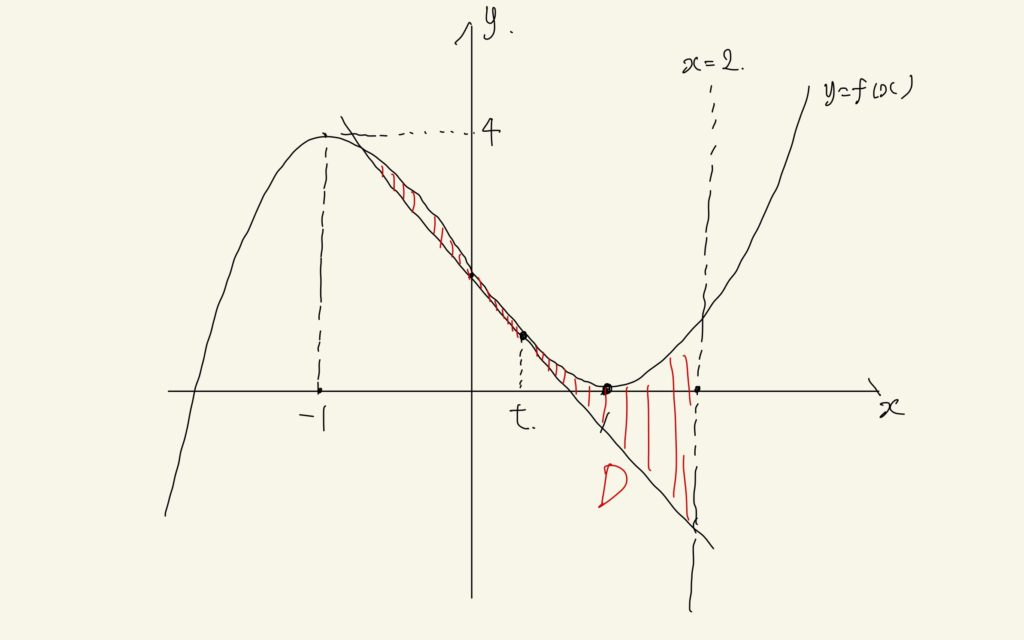
y=f(x)はx=1を極小値とします。また、f'(x)=3x^2-3であることから、x=-1が極大値をとり、その値が4であることもわかります。そこで、上のグラフのような関係です。y=f(x)とy=g(x)にはtの他に、もう1点交点がありますので、これを求めにいきます。そのために、y=g(x)の式を求めます。
$$f'(x)= 3x^{2}-3$$
であることから、x=tを入れたものが接線の傾きです。接点は(t, t^3-3t+2)ですので、y=g(x)の式を求めることができます。
$$g(x)=(3t^{2}-3)(x-t)+t^{3}-3t+2 = (3t^{2}-3)x-2t^{3}+2$$
これと、y=f(x)の交点を求めたいので、f(x)=g(x)とすると
$$x^{3}-3x+2 = (3t^{2}-3)x-2t^{3}+2 \leftrightarrow x^{3}-3t^{2}x+2t^{3} = 0$$
です。意外とスッキリしています。ここで、y=f(x), y=g(x)のもう一つの交点を求めます。色々方法がありますが、解と係数の関係を用いるのが簡明でしょう。x=tは接線なので、f(x)=g(x)における重解となっています。ゆえに、3次方程式の3つの解のうち、2つはtなのでもう一つの解をαとおきます。すると3次方程式の解と係数の関係から
$$\alpha + t + t = 0 \leftrightarrow \alpha = -2t$$
と求めることができます。これで、S(t)を求める準備ができました。あとは難しいことは考えず、とにかくf(x)-g(x)を-2tから2までの範囲で積分しましょう。ここで、f(x)-g(x)は既に求められています。f(x) = g(x)の式を計算するとき、f(x)-g(x)=0となるように移項して計算していたので
$$f(x)-g(x) = x^{3}-3t^{2}x+2t^{3}$$
です。ゆえに求める面積S(t)は次を計算すれば良いです。
$$S(t) = \int_{-2t}^{2}(x^{3}-3t^{2}x+2t^{2})dx$$
$$S(t) = \left[ \frac{x^{4}}{4}-\frac{3t^{2}x^{2}}{2}+2t^{3}x \right]_{-2t}^{2}$$
$$S(t) = (4-6t^{2}+4t^{3})-(4t^{4}-6t^{4}-4t^{4}) = 6t^{4}+4t^{3}-6t^{2}+4$$
です。
(3)
S(t)の最小値を求めたいので、微分して増減表を書きます。
$$S'(t)=24t^{3}+12t^{2}-12t = 12t(2t^{2}+t-1) = 12t(2t-1)(t+1)$$
よって、t=1/2, -1のとき極値を取ることがわかります。0<t<1の範囲で増減表をかくと以下です。

よって
$$t=\frac{1}{2}のとき最小値\frac{27}{8}$$
をとる。最後に、S1:S2を求めます。まず、-2t = -1です。難しいことは考えず、f(x)-g(x)を-1から0まで積分したものを求めましょう。これがS2で、27/8からS2を引いたものがS1です。ただし、t=1/2を代入しておきます。
$$S_{2}= \int_{-1}^{0}(x^{3}-\frac{3}{4}x-\frac{1}{4})dx$$
$$ S_{2}=\left[ \frac{x^{4}}{4} – \frac{3x^{2}}{8} +\frac{x}{4} \right]_{-1}^{0}$$
$$S_{2} = -\frac{1}{4}+\frac{3}{8}+\frac{1}{4} = \frac{3}{8} $$
よって、S1 = 24/8
$$S_{1}:S_{2} = \frac{24}{8}:\frac{3}{8} = 8:1$$
いかがでしょうか。

コメント