高校生3年生にとって最後の夏休みをどのように過ごすかはとても重要です。特に、国公立大学を受験しようと思う場合、センター試験で7科目、二次試験で数科目を対策していく必要があります。この記事では、「特に理系の学生で、数学が得意ではない現役生」または「部活動をしていてこれから本格的に受験勉強を始める学生」が夏休みに何をしたら良いかを考えていきます。学校のカリキュラムは、数学Iから数学Ⅲまで終わっているものとします。
失敗しない夏を過ごすために
夏休みにやるぞ! と思って目の前に並べたものは人それぞれ違うでしょう。学校の教科書、サクシードや4ステップなどの教科書傍用問題集、チャート式、大学への数学、過去問など。「夏休みは時間があるのだから、全ての単元をやり直して数学を得意にしよう!」という計画を立てた人もいると思います。
しかし、本当に夏休みで全ての単元をやりつくすことは可能でしょうか。ちょっと時間の計算をしてみましょう。夏休みは30日程度あるとして、数学に充てられる時間を平均して3時間とします。すると合計90時間、ちょっと多く見積もって100時間を数学に充てる時間と考えます。ところで、3年間の数学の授業は何時間分に相当するかご存知ですか? 学習指導要領の規定では、各学年ごとに5コマ(175時間)×4=700時間と定めています。8月までに1年の半分程度をこなしたとすると、合計1750時間分の時間を数学の習得に費やしたということになります。
ということは、「夏休みで全ての単元をやりつくす」と言っている人は、夏休みの時間に対して17.5倍もの時間をかけて学んできた数学を、たった100時間で復習しようと言っているわけです。これが可能なのは、明らかに「数学が得意で、必要な箇所だけを重点的に補える人」です。数学が得意でない状態から得意にしたいという人にとっては、無謀なことだと言わざるを得ません。
では、どうするか。もし本当に全ての単元をやり直したいという方は、「定期テスト」を3年分やり直すのが手っ取り早いでしょう。定期テストを無くしてしまったという方は数学の先生に連絡すれば、すぐに用意してもらえるはずです。定期テストというのは、学校の先生が、その学校の生徒のボリュームゾーン(平均学力)に合わせて、一生懸命作ったものですから、それを全て解けるようになる実力を身につければ、夏休み以降から始まる「入試演習」の良い準備運動になるはずです。ただ、この方法は確かに「全単元を復習する」良い方法ですが、「入試問題で合格点をとる」という思想からは少し遠のいているかもしれません。皆さんは各大学が全ての単元を「満遍なく出題している」とお考えでしょうか。よくよく入試問題を見てみると、どうやらそうではないことが見えてきます。
入試問題にはバイアス(偏り)がある
大学入試問題は大学教授が作成しています。だから、大学教授が「重要と考える」単元は重点的に狙われやすい。なぜなら、大学が欲しているのは、「高校数学が得意な学生」ではなく「大学に入って学力を伸ばせる学生」だからです。すると、教授の選り好みが出てきます。それが結果的にバイアスとなって入試問題に現れます。最近2年間ほどの国公立大学の理系入試問題の出題傾向をグラフにしました。
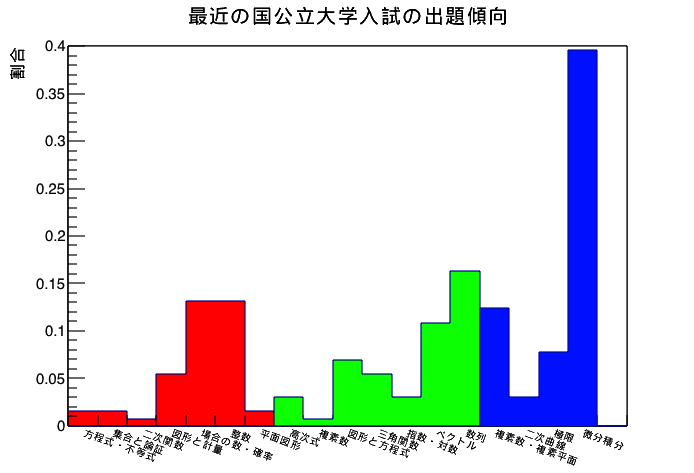
データは裏切らないものです。このプロットは縦軸が1問に対する割合、横軸が単元を示しています。明らかに、「微分積分」の傾向が他に比べて高いことがわかります。その割合が0.4であることは、例えば京都大学や東京大学のように6問を1セットにしている大学では、大問2問分は微分・積分をテーマとしていることを意味しています。また、整数・確率・数列・複素数平面も高い割合で出題されています。数列と確率(場合の数)はよくセットにして出題されるので、その意味で相関があります。
考察
上のプロットからわかることを考えてみます。微分積分がよく出題されることは、大学教授が「微分積分」の習得が高校数学の最大の成果である、と考えていることの裏付けではないでしょうか。実際、どこの大学にしてもほとんど必ず最低1問分は微分・積分そのものをテーマとした問題を出題しています。京都大学や東京大学は最近ではさらにその傾向を強め、「定積分」の問題を出題するほどです。
それならば、受験生はその意図をくみ取り、「微分・積分」の習得を第一に考えるべきでしょう。しかし、「微分・積分」は高校数学3年間の最後に学ぶものであり、現役生にとって十分な訓練が難しい単元でもあります。逆に言えば、最後に学ぶからこそもっとも記憶に新しく、定着させやすいとも言えます。さらに重要なことは「微分・積分」の知識は、他のほとんどの単元とも相関があるということです。言い換えると、他の単元と組み合わせて出題しやすく、「三角関数」をテーマとしているにも関わらず、答えを出す最後のシーンで微分・積分の知識を使うことなんてよくあります。
また、難関大学と呼ばれる大学では、ほとんど必ず「整数問題」「確率・場合の数」を出題してきます。「整数問題」は教科書に、体系的に載っているものではないので、数学的なセンスを問うような出題になることがしばしばです。「確率・場合の数」に関しては、「数列」が絡んだ問題が多いものの、漸化式」を組み上げさせて解くパターンなど、問題の種類に応じて、「ある程度体系化して学ぶことができるので、現役生にとっても得点しやすい単元です。
提案
以上のことから、私の提案はなんとなく予想できると思います。現役生で数学が得意でない生徒が効率よく合格点を勝ち取るために、夏休みにするべきことは以下のことです。
- どの問題集でも構わないのですが、微分・積分の単元を徹底的に解く。この時、計算問題は計算を簡単にする技術を意識しながら解く(これが計算力の向上につながる)。
- 志望校の過去問の中で「微分・積分」に関わる問題を解く。
時間が足りない方は1だけでも十分だと思いますが、秋への演習につなげていく為にも2に手をつけられると良いです。先に述べたように、微分・積分は1年に1~3問程度は出題されるので、これを確実に正解することが現役生の合格の近道だと思います。その上で、数学が得意な人は、数列の絡んだ確率・場合の数、整数へと単元をシフトしていけば良いのではないでしょうか。
とにかく現役生には時間がありません。その中で、最大の効率を得るためには、「出題者の思考」を少しでも汲み取り、それに合わせて勉強をしていくことが肝要です。また、上記の提案は私だけの意見、というわけでもありません。
私が某予備校の授業を受けていた頃、全国的に有名なO先生が、「微分・積分」についてこんなエピソードを持っていました。その先生は高校生の頃とある大学の二次試験で5~6問程度あった数学の問題で、「微分・積分」以外全く解けなかったといいます。しかし、「微分・積分」だけは満点で正解したようです。それで、合格にはならなかったようですが「補欠」で通りました。その後、「繰り上がり合格」の知らせが届いたようですが、すでに別の大学への入学を決めていたため、その大学へは入学しなかったようですが、「微分・積分」の計算力がO先生を合格に導いたという事実に変わりはありません。
数学が得意ではない、または部活動をやっていてこれから本格的に受験勉強を始めようという方へ。
「微分・積分」の習得が王道です。
最後までご覧いただきまして、誠にありがとうございます。

コメント