2007年頃からただただ定積分を解く問題が京都大学で出題されるようになりました。2019年でもその傾向は変わらず、第1問で出題されています。しかもこの問題は2007年の大問1(1)の劣化版のような問題でした。このように、定積分の問題を出題するようになったことから、京大は「発想力」よりも「計算力」を持つ人材、確実に計算を実行できる人材を欲するようになったということでしょうか。特に2011年はその傾向が顕著で、最後の問題以外は受験生なら誰でもすぐに解法が思いつくような問題ばかりで、「確実に計算を合わせる」力が問われていたと思います。
今までの定積分の問題を見ても、そろそろネタが尽きてくる頃で、予想しがいのある頃合いかと思います。そこで、次のような問題を考えてみました。
自問
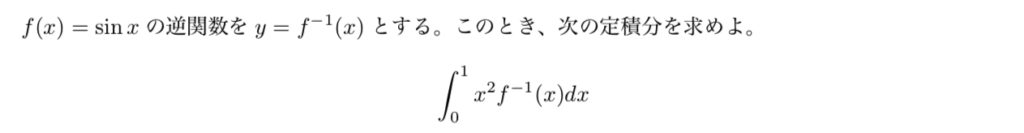
指摘
おそらく長い入試問題の歴史を遡れば、どこかの大学のどこかの年で出題されたことがある問題だとは思います。そもそも2019年の問題が、そのままの形で問題集にも載っているような問題であることを考えれば、定積分の問題では類似性はあまり問われないでしょう。
この問題では逆関数を含んでいますが、逆関数と積分が混合した形はあまり見られないと思いますし、この形の計算自体がそれなりに複雑で、「置換積分」「部分積分」「三角関数の変形」など色々なテーマを含んでいるので京大好みかと思います。難易度は高くないので、是非トライしてみてください。
回答
高校数学の範囲では逆関数は置換をするとうまくいくことが多いです。
$$t=f^{-1}(x)$$
と置換します。置換の作法にしたがって以下の手続きをとります。
$$x=0 \rightarrow t=0,\ x=1 \rightarrow t=\frac{\pi}{2},\ dx = \cos{t}dt$$
$$\int_{0}^{1}x^{2}f^{-1}(x)dx=\int_{0}^{\frac{\pi}{2}}t\cdot\sin^{2}{t}\cos{t}dt$$
$$\int_{0}^{\frac{\pi}{2}}t\cdot\sin^{2}{t}\cos{t}dt=\int_{0}^{\frac{\pi}{2}}t\cdot\left(\frac{1}{3}\sin^{3}{t}\right)^{\prime}dt$$
$$\int_{0}^{\frac{\pi}{2}}t\cdot\left(\frac{1}{3}\sin^{3}{t}\right)^{\prime}dt = \left[t\cdot\frac{1}{3}\sin^{3}{t} \right]^{\frac{\pi}{2}}_{0}-\frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin^{3}{t}dt$$
前半はただ代入をすれば良いだけですが、後半はさらに少し変形して次のように計算します。
$$\frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin^{3}{t}dt = \frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin{t}(1-\cos^{2}{t})$$
$$\frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin{t}(1-\cos^{2}{t}) = \frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin{t}dt-\frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin{t}\cos^{2}{t}$$
$$\frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin{t}(1-\cos^{2}{t}) = \frac{1}{3}\left[-\cos{t}\right]^{\frac{\pi}{2}}_{0}+\frac{1}{9}\left[\cos^{3}{t}\right]_{0}^{\frac{\pi}{2}} = \frac{1}{3}-\frac{1}{9} = \frac{2}{9}$$
よって、先の式に戻って
$$\left[t\cdot\frac{1}{3}\sin^{3}{t} \right]^{\frac{\pi}{2}}_{0}-\frac{1}{3}\int_{0}^{\frac{\pi}{2}}\sin^{3}{t}dt = \frac{\pi}{2}\cdot\frac{1}{3}-\frac{2}{9} = \frac{\pi}{6}-\frac{2}{9}$$
となります。
いかがでしょうか。そもそも私の計算の誤り・論理の不備等ございましたらご指摘いただけると助かります。

コメント