自問

短時間で済ますことのできる数学の自由研究の課題は何だろう。

自答

部活動が多く、数学の自由研究に時間を割くことができない、とか、夏休みも終わり、いよいよ学校が始まるという所になって、残しておいた自由研究の課題を突如思い出して慌ててしまう、ということもあると思います。この記事はそんな中学生・高校生のために、短時間で仕上げることのできる、それなりに有意義な題材を考えてみました。高校3年生は流石に自由研究が課題になることはないと思いますので、他の学年に対応して考えました。気に入ったものがあれば、ぜひ採用して役に立てていただければ幸いです。題材は主に、中学生・高校生が必ず持っているはずの数学の教科書からとってきています。

この記事の目次

中学生のための数学の自由研究課題

中学1年生用

正負の数の概念を日常生活に置き換えて表現する

中学1年生の前半の目玉と言えば、「負の数の導入」に尽きると思います。小学生では、（学習指導要領の範囲内では）マイナスの数というのは扱いません。そこで、大抵の方々は中学生になって初めてマイナスという概念を学校で学びます。その時に次のような計算規則を学ぶはずです。

（正の数）×（正の数）＝（正の数）
（正の数）×（負の数）＝（負の数）
（負の数）×（正の数）＝（負の数）
（負の数）×（負の数）＝（正の数）

1は問題なく理解できると思いますが、2, 3, 4は最初は戸惑うこともあると思います。そこで、これらの概念をなじみやすくするために、日常生活で見られる現象から2, 3, 4に当てはまる事例を探すというのはどうでしょうか。例えば以下のような例があります。

2または3の例

1年ごとに知識が増えていく。昔はものを知らなかったなぁ。

例えば1年ごとに知識量が10だけ増えていくとすると、5年前は今に比べて知識量は$$10\times(-5) = -50$$
だけ少ないという意味。

4の例

1年ごとに記憶力が落ちていく。昔はなんでも覚えられたのになぁ。

例えば1年ごとに記憶力が10だけ落ちていくとする。5年前は今に比べて記憶力は

$$(-10)\times(-5) = 50$$

だけ高いという意味。

こんな感じで、正負の数の概念をなじみやすくするような語録を作っていくと、面白いかもしれません。

中学2年生用

小学生の「なんとか算」の原理を方程式を使って暴き出す

小学生の時に中学受験を経験した人は通称「なんとか算」をひたすら叩き込まれたのではないでしょうか。具体的には

つるかめ算
旅人算
和差算
過不足算
通過算
植木算
仕事算
平均算
相当算
時計算
流水算

などがあります。”小学生　なんとか算”でググれば結構色々見つかります。それで、これらの手法は「方程式という概念を学んでいない」小学生でも解けるものです。しかし、方程式や連立方程式を学んだ中学生2年生なら、この新しい知識を使ってこれらの問題を解くことができるのです。上にあげた1~5まではだいたい、連立方程式を立てることができれば、解くことができるものです。中学二年生のこの時期は連立方程式を学んだ頃合いでしょうし、小学生流の解き方と中学生の「大人の方法」を比較していくというのは面白い試みではないでしょうか。もし「なんとか算」を知らない方は、小学生がどのような苦労（工夫）をして、方程式を使わずにこれらの問題を解くかを知ることができますし、方程式の破壊力を知ることにもなります。

例えばつるかめ算なら次のように比較できますね。

つるかめ算の問題

ツルとカメがいます。頭の数を合わせると20, 足の合計の数は56本です。ツルは何羽でカメは何頭でしょうか。

つるかめ算による解答

ツルの足は2本、カメの足は4本です。どちらも頭は1つなので、もしすべてツルだとすると足の数は40本です。実際には56本の足があるので16本足りません。カメとツルを入れ替えると足の数は2本増えるので、16本増やすにはカメとツルを8だけ入れ替えれば良いです。ゆえに、ツルは12羽でカメは8頭いることがわかりました。

連立方程式による解答

ツルの数を$x$, カメの数を$y$とします。頭の数の合計が20なので
$$x+y = 20$$
足の数の合計が56なので
$$2x+4y = 56$$
これらを解くと$x = 12,\ y=8$となります。

このように、連立方程式は式さえ立てられればまどろっこしい考え方はいらないわけです。他の算法も同じように比較できますので、連立方程式の練習・方程式の練習と思ってやってみると良いと思います。

中学3年生用

中学三年生に自由研究の課題を出すところは多くないと思いますが、もし出されたとしたら受験勉強に時間を使うために、なるべく短時間で済ませたいと思いますよね。中学三年生といえば「二次方程式」「平方根」「放物線」「三平方の定理」など式と計算・方程式・関数・図形のいずれの分野においても「2次数への拡張」が大きなテーマです。そこで、例えば以下のような題材はいかがでしょうか。

根号？　二次式？　なにそれ、美味しいの？

“根号　日常生活”と調べると「なんで根号が必要なのかわからない」「根号なんて日常生活で使わない」という質問やそれに回答する記事がたくさん見つかります。おそらく、理系に興味のない中学生の大半の生徒が同じようなことを考えているのではないでしょうか。

そこで、根号の味を少しでも知っておくために、根号の概念が欠かせない事象について調べてみるというのは良いと思います。

根号の応用例マンホールの形

マンホールは、なぜ丸いのでしょうか。正方形や正三角形じゃダメなのでしょうか。

これを正確に理解しようと思ったら根号が必要です。簡単のため1辺が1の正方形、正三角形と半径が1の円を比べてみます。

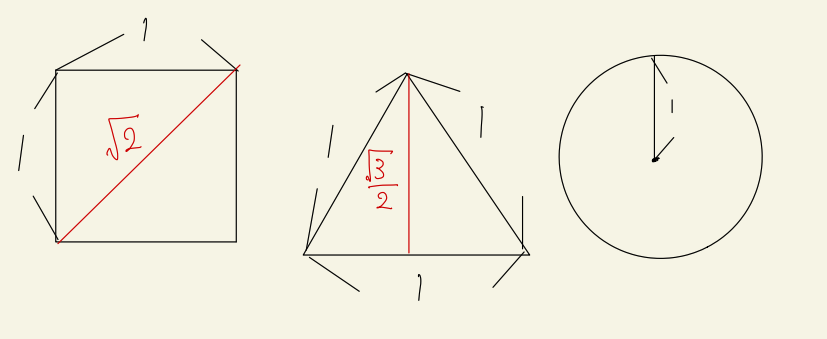
三平方の定理を学んでいれば、正方形の対角線が$\sqrt{2}$, 正三角形の高さが$\frac{3}{2}$となることがわかります。さて、もしマンホールを正方形に設計するとなにが起こるでしょうか。そうです。マンホールとは、下水管の掃除などをする時には一時的に外しておくものですが、もし正方形に作ってしまうと事故で地下にマンホールが落ちてしまうことがあります。平方根を知っていれば、$\sqrt{2} \simeq 1.414$だと知っているので、対角線が辺の長さよりも長いことがわかります。すると、マンホールを対角線に向けて立ててしまうと落ちてしまいます。正三角形の場合も同様です。高さが$\frac{3}{2}$で、これは辺の長さよりも小さいので、やっぱり正三角形を立てると落ちてしまいます。しかし、円の場合は大丈夫です。どのように立てても地下に落ちてしまうことはありません。

このように、根号を知らない人がマンホールを設計すると大変な事故に繋がる危険があります。また、研究課題としては「円よりも良い」形を設計するのも面白いと思います。なにを持って良い、とするかは難しいですが、例えば材料コストを抑えるために「円よりも必要な面積が小さく穴に落ちない設計」を考えてみると面白いと思います。

2次式の応用例　

突然ですが、典型的な高校生の「起床」から「登校」の様子を綴ります。

　目覚し時計が煩い。A君はベッドから起き上がって、1, 2m離れた場所にある目覚し時計を止め、ゆっくりと着替えを始める。途中、机の携帯電話をフローリングの床に落としてしまい、鈍い音がした。着替えを終えたA君は、眠いまなこをこすりながらそれを拾い上げ、一階に降りていく。目玉焼きと味噌汁、それと一杯のご飯を腹に入れ、身支度を整えてから家を出た。
　太陽の日差しが眩しい。電車の時間に間に合うように少し小走りで駅に向かった。途中の交差点で車が飛び出してきたので、慌てて立ち止まる。運転手も急ブレーキをかけ、窓越しに「気をつけろ！」と言いながら走り去った。気分が悪いなぁ、と思いながらともかく駅につき、電車に乗る。加速したり、減速する電車のなかで揺られながら、単語帳を広げて今日のテストに備える。窓から公園のブランコで小さく揺れている少年を見ながら、少し羨ましく思った。
　いつもの駅で降り、通学路を歩いていると後ろから友達に声をかけられた。そいつはA4のプリント用紙を持ちながら、「今日のテストどうだい？」と聞いてくる。「まぁ、大丈夫じゃない」と適当に返事をしながら二人で学校に向かう。駅から学校までは一本道で、最初は数cmほどの大きさだった学校がどんどん大きくなっていく。今日もいいことがあるといいな。

さて、問題です。この文章中に、”根号または2次式”と関わりの深い現象はいくつあるでしょう？

実は少なくとも僕の理解の中では、”X個”あります。それぞれあげてみましょう。

その１　目覚し時計の音

目覚し時計のような等方的に音を鳴らすものの場合、音の強度と距離は2乗に反比例しています。すなわち音の強度をD, 距離をRとするとある定数kを用いて
$$D = \frac{k}{R^{2}} \leftrightarrow R = \sqrt{\frac{k}{D}}$$
となっています。

その２　携帯電話をフローリングの床に落とす

このとき、携帯電話（質量$m$）がフローリングの床までに達した時の速さを$v$, その時の運動エネルギーを$E$とすると次の関係があります。
$$E =\frac{1}{2}mv^{2}$$
運動エネルギーとは、運動するときに発生するエネルギーと考えれば良いです。

その3 太陽の日差しが眩しい

これは音の話と似ていますが、太陽からでる光の強度と太陽からの距離は2乗に反比例するという法則があり、その１と同じような式が出てきます。

その４　車の急ブレーキ

車が急ブレーキをかけたとき、ブレーキをかける前の速度$v$と止まるまでの距離$D$とにはある定数$k$を用いて次の関係があります。
$$D = kv^{2}$$

その5　電車の加速・減速

電車が加速したり、減速したりするとき、電車の速度と進む距離は2次式の関係があります。高校物理の話になるので、詳しくは割愛します。

その6　公園のブランコで小さく揺れる少年

公園のブランコは小さく揺れていれば、およそ振り子と考えることができます。振り子の周期$T$は、定数$k$, 始点からの長さ$l$を用いると
$$T = k\sqrt{l}$$
と表せます。

その7　A4のプリント用紙

A4のプリント用紙は白銀比と呼ばれる比で横と縦の長さが決まっています。白銀比とは横の長さと縦の長さの比が$1:\sqrt{2}$となっているもののことです。このようにすると面白いメリットがあります。

その８　学校の大きさと距離

学校の見かけの大きさは、音や光の強度の話と似ていて、距離の2乗に反比例しています。

このように、普通の高校生の日常生活の本の一部を切り取っただけでも、根号や2次数にまつわる話にありふれています。その他、弦楽器の調律、黄金比、地球脱出速度とエネルギーの関係など根号や2次式の概念を使わないと理解できないことがたくさんあります。それらを見つけてみるのは、夏休みの課題に適していると思います。また上の関係性をもっと詳しく調べてみるだけでも十分な自由研究ではないでしょうか。

高校生のための自由研究課題

高校1年生用

ラングレーの問題を解いてみる

ラングレーの問題は本ブログでも紹介していますが、”ラングレーの問題”と検索すれば、たくさんの記事が見つかります。いくらでも解法パターンがあるので、一度挑戦してみると面白いかもしれません。

数学マジックを説き明かせ

高校生では整数の問題を取り扱うことが増えてきます。その時に整数の倍数の性質を知っていると便利なことが多いです。整数の扱いになれるという意味で、数学マジックを考えたり、その原理を考えていくのは面白いと思います。例えば次のようなマジックがあります。

数学マジック

ここに9216という数字があります。好きな4けたを思い描いてください。その4けたの数と9216をかけて整数を作ってください。それは、8けたになると思いますそのうちの7けたを、順番はデタラメで良いので僕に教えてください。

（9216×5548 = 51130368だから……）5, 0, 1, 3, 1, 6, 3

残りの数は”8″ですね！

上のマジックはとてもシンプルな原理に基づいていますので、数学の倍数性に長けていれば自然と種が見えてくると思います。実際に原理を解析して、実践してみるのも面白いですね。

高校2年生用

面白い定理や公式を示す

高校2年生の夏の時期ですと、指数・対数関数や三角関数を学ぶでしょう。ここまでくると日常生活に応用する、というよりは学校で習わないが面白い公式や定理を証明してみるという方法があります。

三角関数の定理1

三角形ABCの外接円の半径をR, 内接円の半径をrとする。このとき
$$\cos{A}+\cos{B}+\cos{C}=\frac{R+r}{R}$$
が成り立つ。

三角関数の定理2

$$\tan{a}+\tan{b} = \frac{\sin(a+b)}{\cos{a}\cos{b}}$$

三角関数の定理3

$$\sin{20^{\circ}}\cdot\sin{40^{\circ}}\cdot\sin{80^{\circ}} = \sqrt{\frac{3}{8}}$$

や

$$\cos{20^{\circ}}\cdot\cos{40^{\circ}}\cdot\cos{80^{\circ}} = \frac{1}{8}$$

など、特別の角に対する特別の値

カイジに登場する金利の計算を理解せよ

指数といえば、金利の処理がよくテーマに上げられます。特に”複利”という考え方は重要で、これを理解せずにお金を借りようものなら、地獄の底の底、一月91000ペリカで暮らす地下での強制労働が待っています。

逆境無頼「カイジ」というアニメでは、借金の話がひっきりなしに出てくるので、鬼のような金利がいくつもあります。アニメの中では一瞬でその計算が行われていますが、その計算についていけてる人はほとんどいないでしょう。もし、指数と数列の話を学んでいるのなら次の計算を手でやってみて、シリーズの話と整合性を確かめてみるのは面白いかもしれません。

限定ジャンケンでの10分1.5%の複利

限定ジャンケンのゲーム時間は4時間。1000万を元手に10分1.5%の複利で増え続けるとするとき、最終的な金利の合計はいくらか。

パチンコ”沼”における遠藤さんの10分3割複利

1000万円を元手に10分3割複利で金利を回す。92分後にゲームが決着したら借金はいくらか。

これらの金利を、通常の貸し金業者の金利と比較してみると、登場人物たちの嘆きがよくわかると思います。

終わりに

数学の自由研究で短時間でできそうなものを上げてきましたが、中には少し厄介なものもあったかもしれません（中には自由研究としてふさわしいのかどうか怪しいものもあると思います。その場合は学校の先生と要相談……）。今後新しく思いついたものがあれば、どんどん更新していこうと思います。質問等ありましたら、ぜひコメントしていただけると嬉しいです。