問題リクエスト
1. 巻線比 15,一次巻線の抵抗 20.0[Ω],漏れリアクタンス 15.0[Ω],二次巻線の抵抗 0.10[Ω],漏れリアクタンス 0.06[Ω]の変圧器がある。この変圧 器に 6600[V]の電源を接続し,二次巻線の端子に 8.0[Ω]の抵抗と 6.0[Ω]のリア クタンスを直列に接続した。実際の一次電流,二次電流,二次電圧を求めよ。 ただし,励磁電流は小さく無視できる。
2. 定格容量 300[kVA],定格二次電圧 6.6[kV],定格力率 0.8,定格時の鉄損 1600[W],負荷損 3600[W]の単相変圧器がある。次の値を求めよ。
①定格二次電流と定格時の効率
②出力 200[kW],負荷の力率 0.8 ときの二次電流と効率
ただし,二次電圧は定格二次電圧のままとする。
リアクタンスとインピーダンス
中学までの物理では、電圧を電流で割ると常に一定の値となり、この値を抵抗と呼んで電流の流れにくさを表すものだと教えられています。高校に入ると、電圧と電流は常に一定になるわけではなく、温度による揺らぎによって、電圧と電流の比は常に一定になるとは限らないことを学びます。一定にならなくとも、ある時点における抵抗の値は電圧を電流で割ったものとして定義されます。いずれも電流の流れが時間に依存せず、常に一定の向きを持っていました。
高校物理の最終盤では、「交流回路」が登場します。そこでは、電流の向きが時間とともに変化します。特に、コンデンサーやコイルが加わった回路では、直流回路での抵抗という概念だけではもはや、「電流」と「電圧」の関係を考えることができなくなります。この記事では変圧器を取り扱うので、特に関わりが深いコイルが加わった回路を考えます。
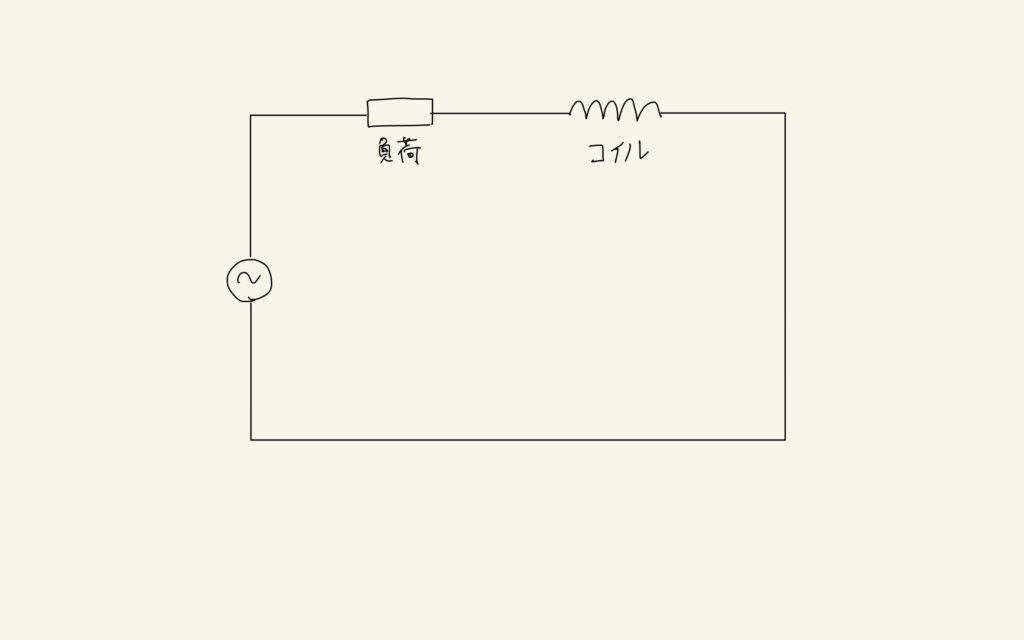
このような単純な回路でも、電流と電圧の関係はそれほど単純ではありません。電圧は電源から供給されますが、交流回路では、時事刻々と電流が変化するので、それに応じてコイルの振る舞いが変わります。コイルは「誘導起電力」により回路に流れる電流を抑制したり、増加させたりするので、そのようなコイルの振る舞いによって電流が決まります。すなわち、直流回路のように与えられた電圧を負荷の抵抗で割れば電流が求められる、というものではなくなります。
回路に与える電圧、コイルの誘導起電力を定式化して電流と電圧の式を求めると、コイルに関係するある物理量が負荷で定義されたような「抵抗」と同じ関係にあるということがわかります。このようにコイルで「抵抗」のような働きをする物理量を「リアクタンス」と言います(リアクタンスはコンデンサーについても定義されます)。回路内における、負荷の抵抗と全てのリアクタンスを合わせたものを「インピーダンス」と呼んでおり、このインピーダンスを導入すると、コイルを含んだ回路でも直流回路と似たような方法で電圧と電流の関係を考えることができます。すなわち、ある電圧\(V\)に対して、回路のインピーダンス\(Z\)が求められれば、電流は\(V/Z\)で計算できるわけです。
すなわち、コイルなどを含んだ回路で電流と電圧の関係を考えたいのであれば、回路全体のインピーダンスを求めることが重要な手続きです。インピーダンスは、抵抗と全てのリアクタンスを合わせたもの、と表現しましたが、この表現は正確ではないかもしれません。「合わせる」というのは足し算を匂わせる言葉ですが、回路内の全ての抵抗とリアクタンスを「足し算」しても、インピーダンスにはなりません。これは、コイルのリアクタンスが「ベクトル量」であることから来ています。直流回路において、抵抗を何個か直列に接続した時に全体の抵抗が\(R_{1}+R_{2}+R_{3}\)のように足し算の形でかけたのは、それぞれの抵抗値が「スカラー量」と呼ばれるただの「数」だったためです。「ベクトル量」というのは、普通高校二年生で学びますが、「向き」と「大きさ」の両方の性質を併せ持つ量のことを言います。一般にベクトル量は「矢印」で表して、矢印の向きがベクトル量の向きであり、矢印の長さが大きさを表します。
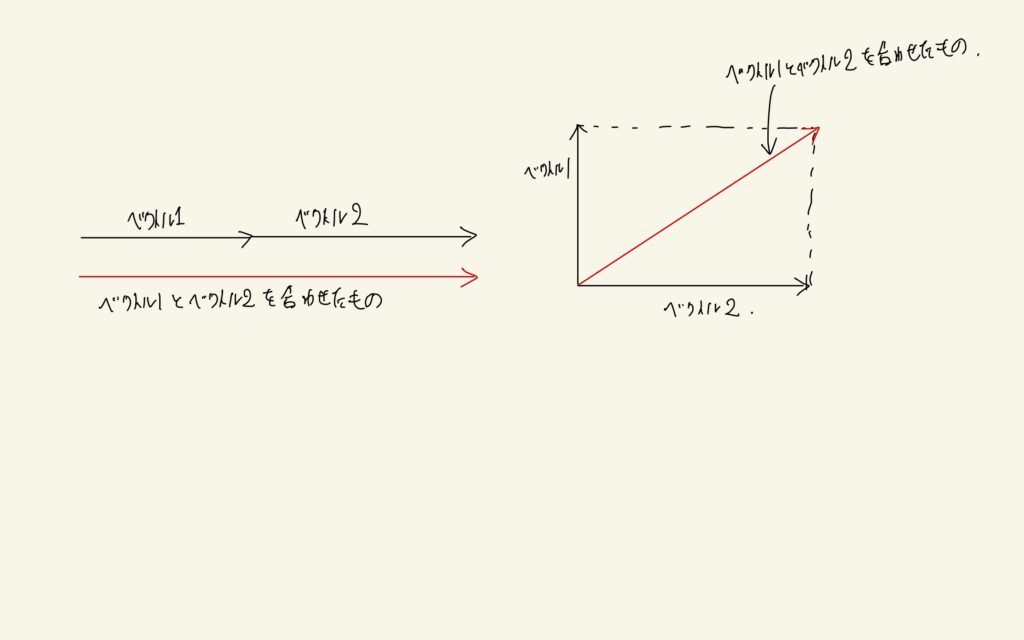
もし、矢印の向きが同じであれば、その大きさを求めることは単純で、単に大きさを足し算すればいいです。直流電源の直列回路の全体抵抗を求めるというのは、その例の一つと考えることができます。しかし、矢印の向きが異なると、単純な足し算では大きさが求められません。コイルを含んだ交流回路では、抵抗のもつリアクタンスとコイルの持つリアクタンスが「異なる向き」であることを理解しておく必要があります。さらに、その向きは通常「直角」であることが重要です。すなわち、上の図の右側がその状況を表しています。ベクトル1が抵抗のリアクタンス(大きさを\(A\))、ベクトル2がコイルのリアクタンス(大きさを\(B\))と考えます。この二つを合わせたものが回路全体のインピーダンスであり、その大きさは三平方の定理により\(\sqrt{A^{2}+B^{2}}\)と与えられます。このようにして求められたインピーダンスを用いると、ある定格電圧\(V\)に対する定格電流\(I\)は
$$I = \frac{V}{\sqrt{A^{2}+B^{2}}}$$
と求めることができます。変圧器の漏れリアクタンスを考慮する問題では、このような計算が特に重要となります。漏れリアクタンスは、1次側と2次側のコイルを貫通する磁束とは別にそれぞれのコイルに発生してしまう「漏れ磁束」が原因で、本来の電流の流れを阻害する働きをします。
単相変圧器の等価回路
1次換算
単相変圧器は通常次のような回路図で表現できます。
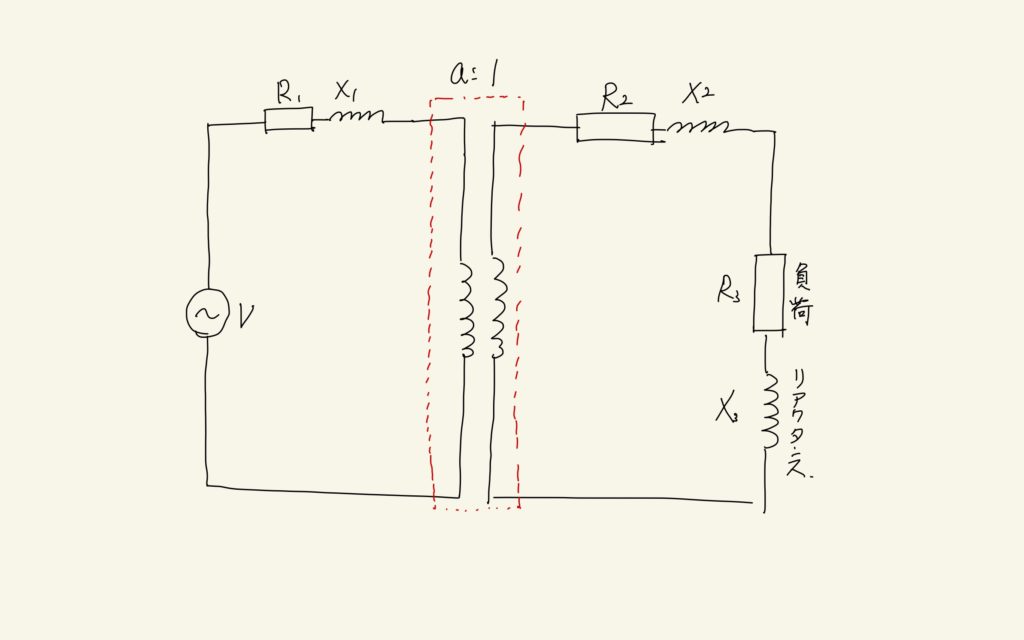
ここで、1次側と2次側の巻数比が\(a\)であるとします。さて、1次側に定格電圧Vがかけられた時の1次側の電流値を求めるためには、2次側にある全ての負荷とリアクタンスが1次側にあると仮定した時の全体のインピーダンスを求めることが必要です。とはいえ、この回路が二つに分離されているので、2次側の負荷やリアクタンスをそのまま1次側に移すわけにもいきません。そこで、1次側と2次側を「仮想的につないだ」回路を考えることにします。このような回路を等価回路と呼びます。それでは、等価回路の作り方を説明してみます。

簡単のため、上のような単純な単相変圧器を仮定します。上の回路図では、1次側に負荷もリアクタンスもありませんが、2次側に抵抗\(R\)の負荷があります。この時に、1次側に発生する電流を求めるためには、二つの方法があります。一つ目は、はじめに2次側で発生する電圧および電流を求め、巻数比を用いて1次電流を求める方法です。二つ目は、2次側の負荷があたかも1次側にあるかのように回路図を組み直して、1次側の電圧をそのまま用いて計算するというものです。最初に、一つ目の方法を試します。
1次側の電圧は\(V\)であることから巻数比を用いると2次側の起電力は\(\frac{V}{a}\)と求められます。ゆえに2次側に流れる電流は
$$\frac{V}{aR}$$
となり、巻数比の関係から1次側に流れる電流はこの\(\frac{1}{a}\)倍になるので
$$\frac{V}{a^{2}R}$$
と求められます。これをヒントにすると、上の単相変圧器の回路は次のように置き換えることができます。
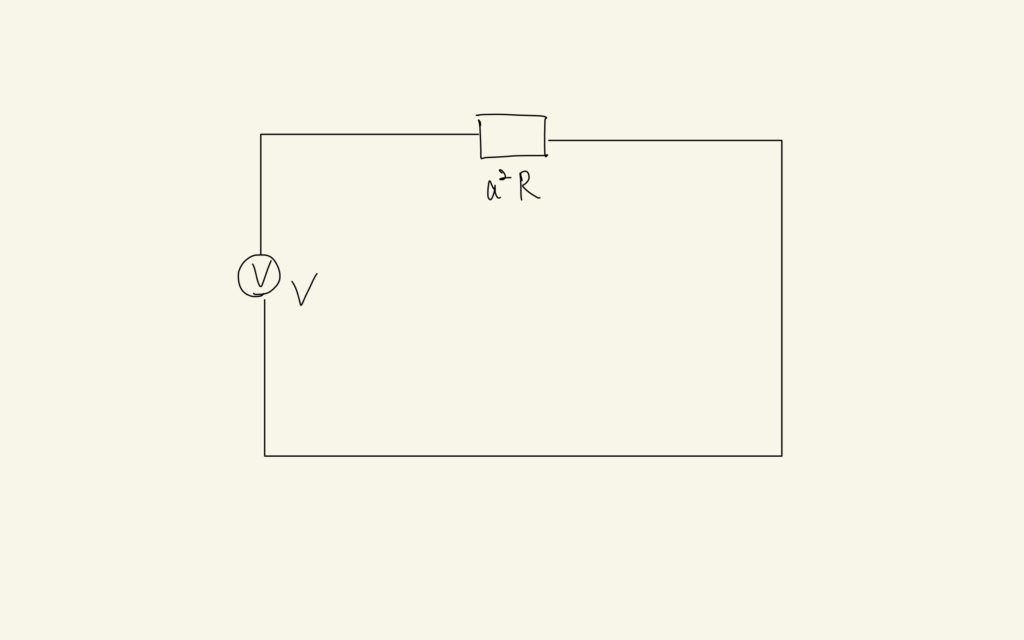
すなわち、1次側に\(a^{2}R\)の大きさをもつ抵抗があり、そこに\(V\)の電圧がかかっているという状況です。この場合の電流は同様に
$$\frac{V}{a^{2}R}$$
と求められます。これが二つ目の方法に対応しています。このように2次側にある負荷やリアクタンスを1次側にあるものと思って回路図を組み直す(換算する)時は、巻数比の2乗をかけることで等価回路を作ることができます。
2次換算
逆に1次側の負荷やリアクタンスを2次側に換算する場合も考えておきます。
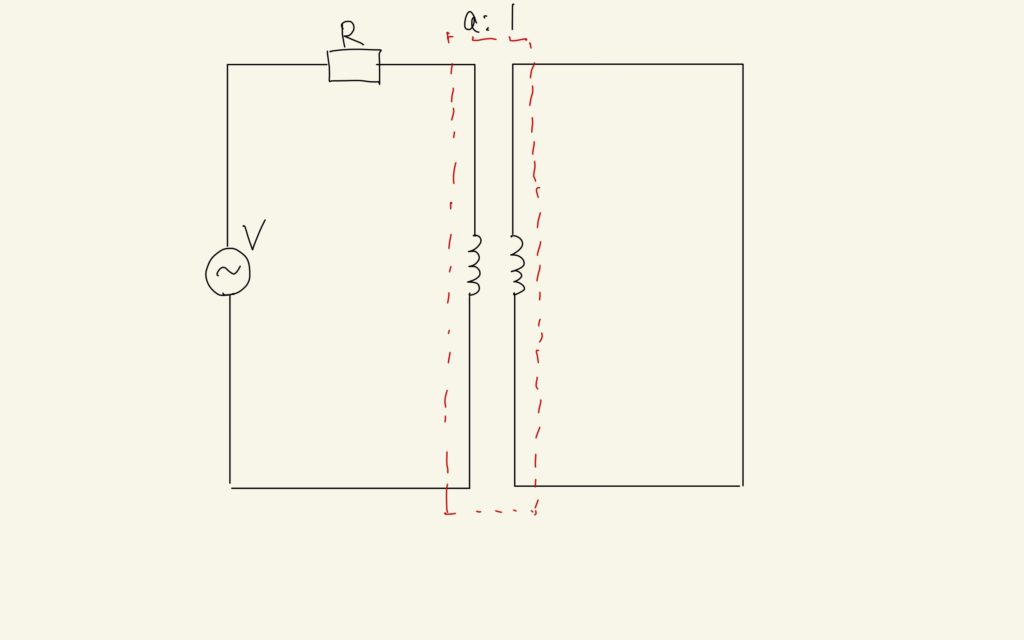
1次側の電流は\(\frac{V}{R}\)と求められるので、2次側の電流はその巻数比から
$$\frac{aV}{R}$$
と求められます。これをヒントに、2次側の電圧が\(\frac{V}{a}\)となることに注意して等価回路を作ると以下のようになります。
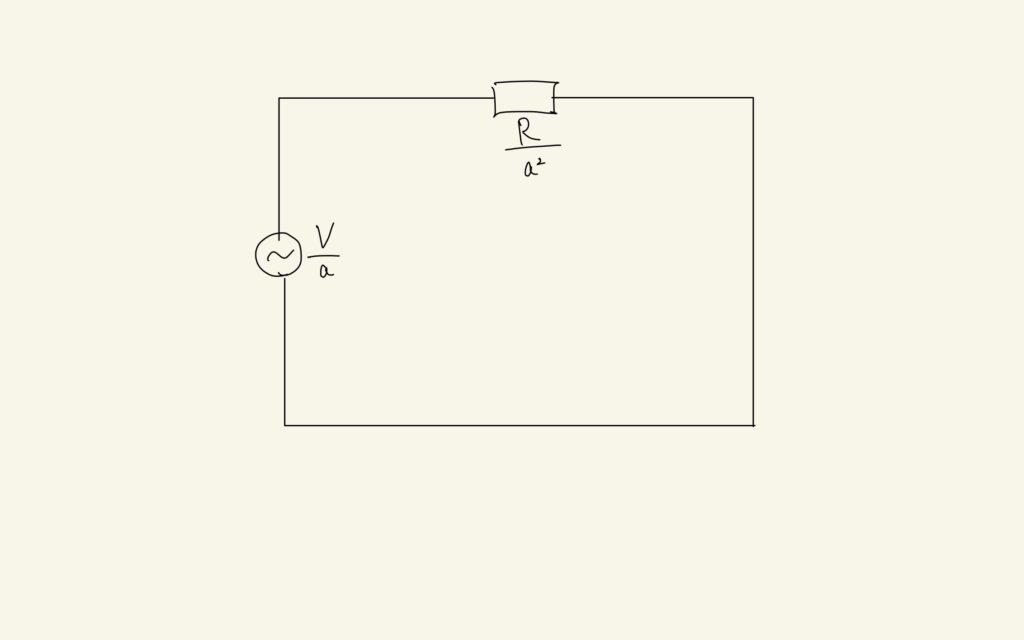
このように、1次側にある抵抗を2次側に持ってくるためには\(a^{2}\)で割った値を用いることになります。ここでは負荷しか扱いませんでしたが、リアクタンスについても同様の関係が成り立ちます。
変圧器の効率と力率
発電機や電動機と同様に、変圧器でも効率を考えることは設計上でとても重要です。計算の概念は基本的に発電機や電動機のそれと同じで、全体の入力に対する出力の割合を計算します。効率には、「実測効率」、「規約効率」または「全日効率」など様々な定義がありますが、主にリクエスト問題に関わる効率の計算では「規約効率」で定義されるものを計算します。規約効率では、入力は出力と損失の和で与えられ、損失には鉄損と銅損を考慮します。鉄損や銅損は回路内の熱や振動に伴うエネルギーとして消費されます。規約効率を求める公式は以下で与えられます。
$$\eta = \frac{P}{P+P_{a}+P_{b}}$$
ここで、\(P\)は出力、\(P_{a}\)は鉄損、\(P_{b}\)は銅損です。もし負荷に電圧\(V\)、電流\(I\)が流れているならば、理想的な状況では\(P=VI\)と計算できます。しかし、実際の電気機器では、供給される電力全てを消費できるとは限りません。電気機器内においては熱などの不要なエネルギーに変換されてしまうものもあるからです。これを考慮したものが力率という概念です。力率は与えられた電力に対して、その機器が有効に使える電力の割合を表すようなもので、
$$\cos{\theta} = \frac{VI_{\mathrm{eff}}}{VI}$$
と与えられます。ゆえに実際の出力\(VI_{\mathrm{eff}}\)は理論的な電力に力率をかけたもの\(VI\cos{\theta}\)で表されます。これを用いると規約効率は
$$\eta = \frac{VI\cos{\theta}}{VI\cos{\theta}+P_{a}+P_{b}}$$
と書き直すことができます。
リクエスト問題の回答
問題1
巻線比 15,一次巻線の抵抗 20.0[Ω],漏れリアクタンス 15.0[Ω],二次巻線の抵抗 0.10[Ω],漏れリアクタンス 0.06[Ω]の変圧器がある。この変圧 器に 6600[V]の電源を接続し,二次巻線の端子に 8.0[Ω]の抵抗と 6.0[Ω]のリア クタンスを直列に接続した。実際の一次電流,二次電流,二次電圧を求めよ。 ただし,励磁電流は小さく無視できる。
この問題では、単相変圧器を「理想的な変圧器」としてではなく「漏れリアクタンス」を考慮した実際の変圧器の応答として計算をする必要があるので、慎重に考えていく必要があります。まず、上の問題文で出てきた変圧器の構造を回路図に書き直してみます。励磁電流は小さく無視できるとあるので、励磁部分については無視します。
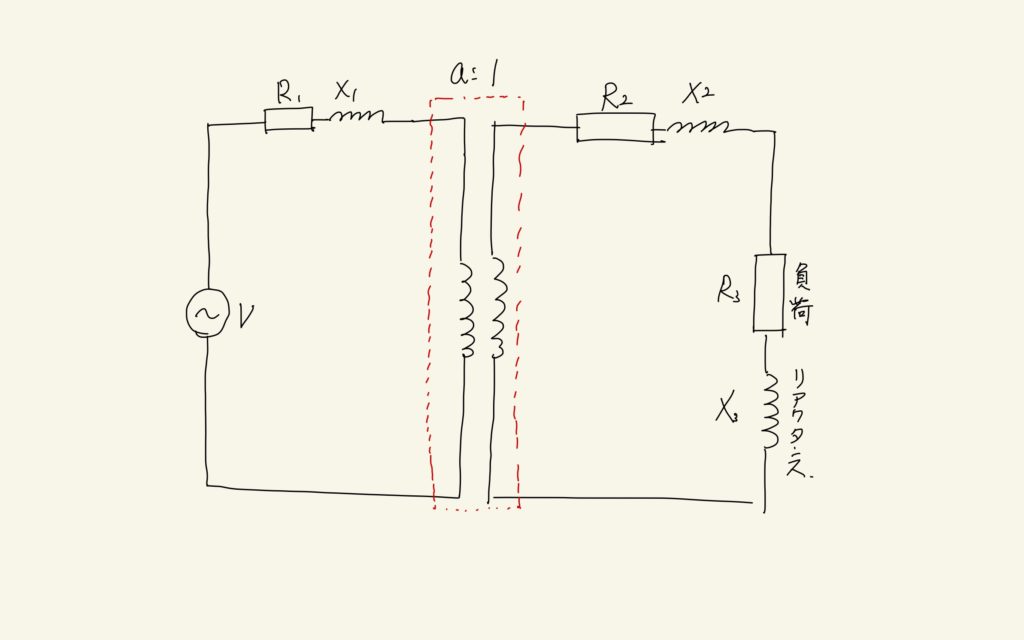
\(R_{1}, R_{2}\)はそれぞれ巻線の抵抗、\(X_{1}, X_{2}\)は漏れリアクタンスの抵抗、\(a\)は巻数比です。\(R_{3}\)は負荷の抵抗、\(X_{3}\)はリアクタンスです。またこの回路にはVだけの電圧が加わるとします。これは1次電圧に相当します。この問題の肝は、どのようにして1次電流を求めるか、ということにあります。1次電流を求めることができれば、2次電流は巻数比から容易に求められ、また二次電圧も求めることができます。1次電流を求めるためには、通常、1次側に換算した等価回路を用いてインピーダンスを求め、それと1次電圧を用いて計算することが常套手となります。そこで、以下のように等価回路を書いておきます。
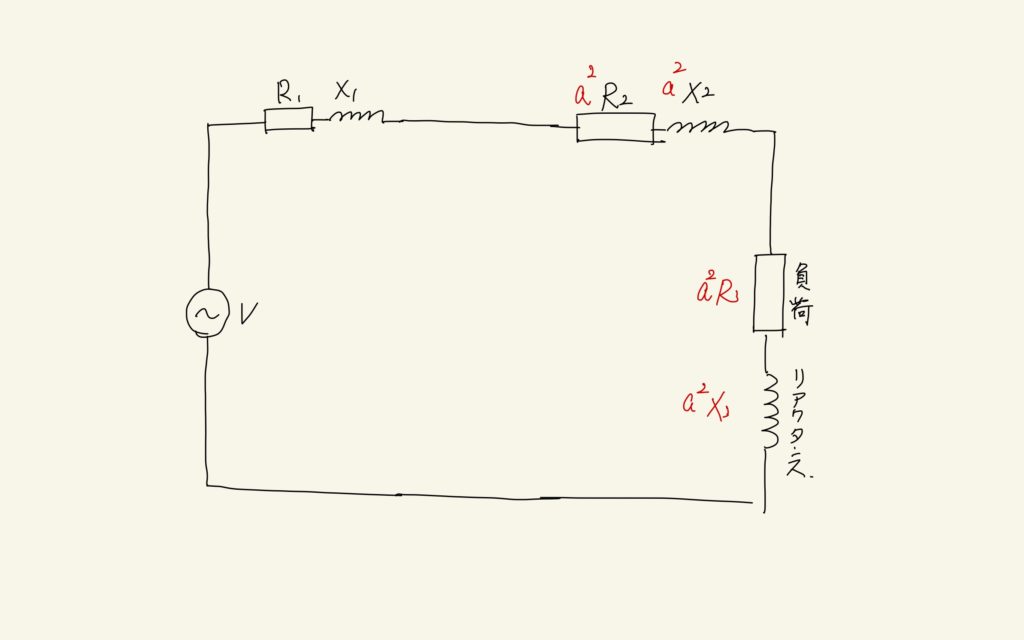
等価回路のところで触れたように、1次側に換算した等価回路では、2次側にあるそれぞれの抵抗やリアクタンスを\(a^{2}\)倍することが必要です。ここで1次側に換算する理由は、現在1次電圧が与えられており、問題として1次電流を求めることを目的としているためです。等価回路がかけたので、それぞれの抵抗の和、およびリアクタンスの和を求めます。
$$R = R_{1}+a^{2}R_{2}+a^{2}R_{3} = 1842.5 (\Omega), X = X_{1}+a^{2}X_{2}+a^{2}X_{3} = 1378.5 (\Omega)$$
抵抗とリアクタンスがそれぞれ直交する向きをもつベクトル量であることを思い出すと、この回路のインピーダンス\(Z\)を求めるためには、三平方の定理を使うことができます。
$$Z = \sqrt{R^{2}+X^{2}} \simeq 2301$$
インピーダンスが、この回路での実質上の全体抵抗を表すので、1次電流は1次電圧6600 Vを用いると
$$I_{1} = \frac{V_{1}}{Z} = \frac{6600}{2301} = 2.868 \simeq 2.87 (\mathrm{A})$$
より、有効数字3けたで表すと2.87 Aとなります。2次電流は巻数比から求められるので
$$I_{2} = I_{1}\times 15 \simeq 43.0 $$
より43.0 Aです。次に2次電圧を、順を追って求めていきます。2次電圧とは、この場合二次巻線の端子にかかる電圧のことでしょう。1次側での巻線抵抗およびリアクタンスによる電圧降下を考慮すると、変圧器の部分にかかる電圧は
$$V^{\prime} = V-\sqrt{R_{1}^{2}+X_{1}^{2}}\times I_{1} = 6600 – \sqrt{20^{2}+15^{2}}\times 2.868 \simeq 6528 (\mathrm{V})$$
です。ここで1次側での抵抗とリアクタンスを考慮したインピーダンスを三平方の定理で求め、それに1次電流をかけて電圧降下を求めています。これをさらに2次側に伝搬すると巻数比から
$$V^{\prime\prime} = 6528/15 \simeq 435.2 (\mathrm{V})$$
となり、2次巻線とリアクタンスの電圧降下の分だけ引けば2次電圧となります。2次巻線とリアクタンスを考慮したインピーダンスに\(I_{2}\)をかけると電圧降下が求められるので、この値を\(V^{\prime\prime}\)から引くと
$$435.2 – \sqrt{0.1^{2}+0.06^{2}}\times 43.0 \simeq 430 (\mathrm{V})$$
より、求める2次電圧は430 Vと計算できます。
問題2
定格容量 300[kVA],定格二次電圧 6.6[kV],定格力率 0.8,定格時の鉄損 1600[W],負荷損 3600[W]の単相変圧器がある。次の値を求めよ。
1. 定格二次電流と定格時の効率
2. 出力 200[kW],負荷の力率 0.8 ときの二次電流と効率
ただし,二次電圧は定格二次電圧のままとする。
この問題では、定格容量(定格電力)と定格二次電圧が与えられているので、ここから定格二次電流を求めることができます。定格容量は定格二次電圧と定格二次電流の積で表されるので、\(I = 300/6.6 \simeq 45.5 (\mathrm{A})\)です。定格時の効率を求める公式は
$$\eta = \frac{VI\cos{\theta}}{VI\cos{\theta}+P_{a}+P_{b}}$$
を用います。今、\(VI = 300\times 10^{3}\) (W), \(\cos{\theta} = 0.8\), \(P_{a} = 1600\) (W), \(P_{b} = 3600\) (W)と与えられているのでこれらを代入すると
$$\eta = \frac{300\times10^{3}\times0.8}{300\times10^{3}\times0.8+1600+3600} \simeq 0.9787 \simeq 0.979$$
より効率は97.9%と求められます。2の問題は出力の値を変更すればよいので二次電流は
$$I = \frac{200}{6.6} \simeq 30.3 (\mathrm{A})$$
であり、効率は
$$\eta = \frac{200\times10^{3}\times0.8}{200\times10^{3}\times0.8+1600+3600} \simeq 0.9685 \simeq 0.969$$
96.9%となります。
終わりに
このトピックに関しては、私も初めて学びました。いろいろな資料を調べながら回答しましたが、議論の誤りや計算のミスなど発見された場合はコメント欄で修正していただけると幸いです。よろしくお願いします。

コメント