今日は、確率漸化式の問題を解こうよ。
ん〜、その前に、確率漸化式の解き方を説明してほしいな。
じゃあ、漸化式の性質をまず考えてみよう!
1. \(P_{n+1} = aP_{n} + C\)のような関係となるものを2項間漸化式
2. \(P_{n+2} = aP_{n+1} + bP_{n}\)のような関係となるものを3項間漸化式
という。
漸化式っていうのは、前の試行と後の試行に何らかの関係性がある時に立てられるものなんだよ。別の言い方をすると、前後の試行に何らかの「縛り」「ルール」があるって場合だね。逆にいうと、こういう「縛り」があるときは、漸化式を使える可能性が高いってことだね。
縛り、ねぇ。あんまり、イメージできないなぁ。
じゃあ、京大のとっても有名な問題でイメージしてもらお。
2007年乙 第1問(2) 階段を駆け上がれ!でもゆっくりね。
問題
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15個の階段を昇り昇り方は何通りあるか。
さぁ、縛りを見つけてみよう!
1歩で2段昇ることは連続しないってこと?
正解! これって立派な縛りじゃない? だって、1個前が2段飛びだったら、次は絶対1段飛びってことでしょ。関係性があるじゃん。この関係性を使うんだよ。
なるほど。それで、どうやって式を立てるの?
漸化式の立て方は大きく分けて2パターンあるよ。
2. 最後の一歩で場合分け
意識しとけばいいのはこんくらいかな。一応、どっちに分類されるかって特徴があるけど、両方試してうまくいく方でやればいいんだよ。ちなみに、図でイメージしてもらうと、こんな感じかな。
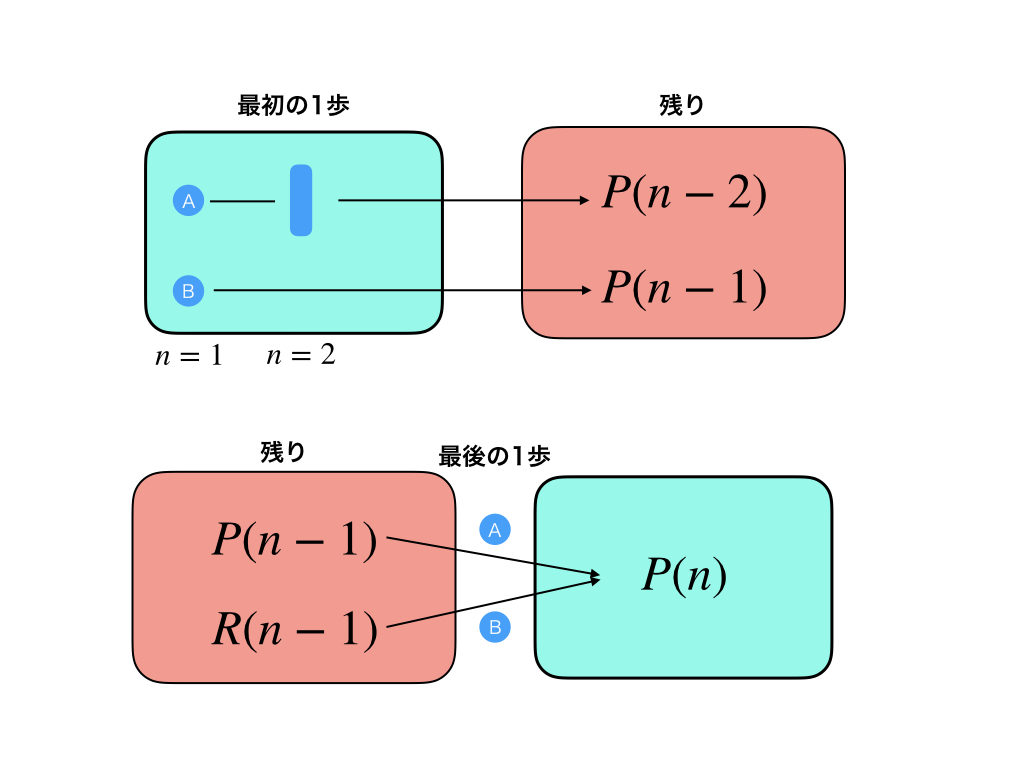
傾向としては、場合の数の漸化式が立てられるときは、「最初の一歩で場合分け」、確率漸化式が立てられるときは、「最後の一歩で場合分け」になりやすい気がする。確率漸化式のときは、\(R(n-1) = 1-P(n-1)\)になっていることも多いね。それと最後の一歩で場合分けをするときは、\(n-1\)回目までの試行をひっくるめて\(P(n-1)\)とできるときだね。今回はどうかな?
う〜ん。\(n-1\)段目までののぼり方を\(P(n-1)\)としちゃうと、\(n-1\)段目までに1段飛びできたのか、2段飛びできたのかわからないから、ちょっと面倒かも。
そうそう、その感覚ね。じゃあ、最初の一歩を考えようってことになるよね。
じゃあ、図を書いてみるね。
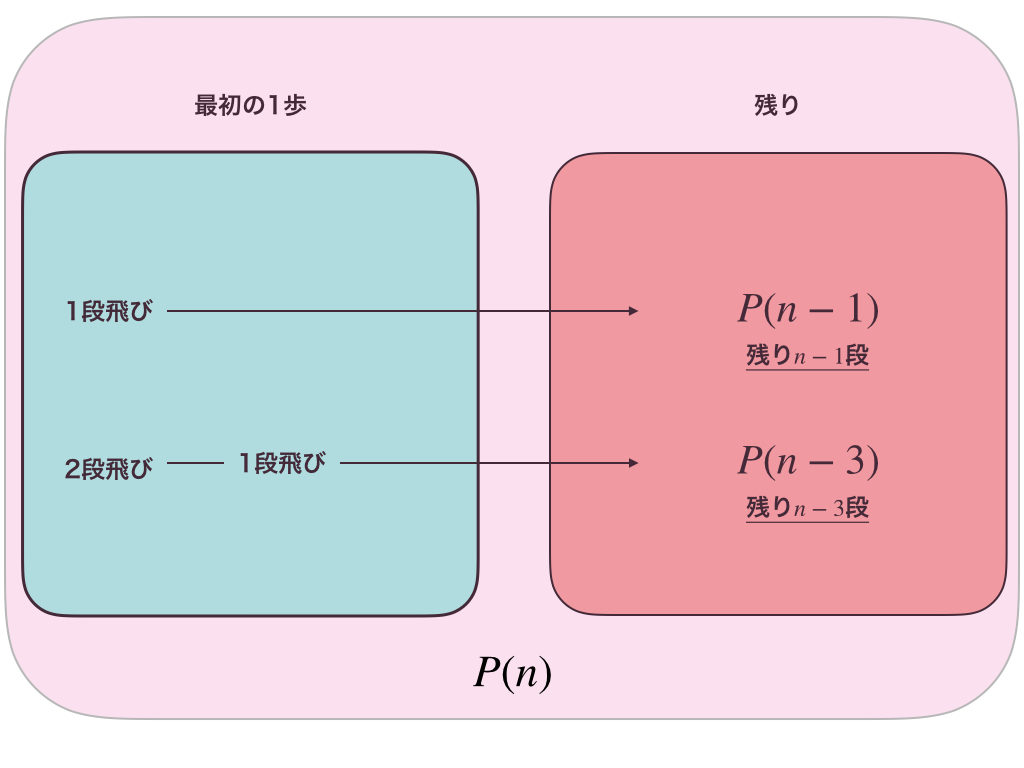
うん、こうやって書けば
$$P(n)=P(n-1)+P(n-3)$$
だってことがわかるね。
そういうこと! きっちり、縛りを使ったでしょ。この問題の場合は\(n\)が15とわかっているから、この漸化式を解く必要はないよね。必要なのは、
$$P(1), P(2), P(3)$$
だね。これらはすぐにわかって
$$P(1) = 1, P(2) = 2, P(3) = 3$$
だから、あとはP(4)から順番に求めていけばいいね。
そうだね。順番にやっていくと\(P(15)=277\)だよね。
これで、わかったよね? 縛りの使い方と、「漸化式」の立て方を抑えれば、この手の問題は解ききれるんだ。
おっけい。ちょっとわかってきた。じゃあ、次の問題いこっ。
2005年 第6問 赤色大好き! 色ぬり職人
問題
先頭車両から順に1から\(n\)までの番号のついた\(n\)両編成の列車がある。ただし、\(n\geq2\)とする。各車両を赤色、青色、黄色のいずれか一色で塗るとき、隣あった車両の少なくとも一方が赤色となるような塗り方は何通りか。
さぁ、縛りを探そう!
隣あった車両の少なくとも一方が赤色ってところだね。
その通り。じゃあ、今回ははじめの一歩かな? それとも最後の一歩かな?
う〜ん。今回も\(P(n)\)って置いちゃうと、\(n\)両目が赤色かどうかわからないから、やっぱりはじめの1歩かな。最初が青色か黄色なら次は赤色だし、最初が赤色なら次はなんでもいいしね。
よし、じゃあ、図を書いてみよう!
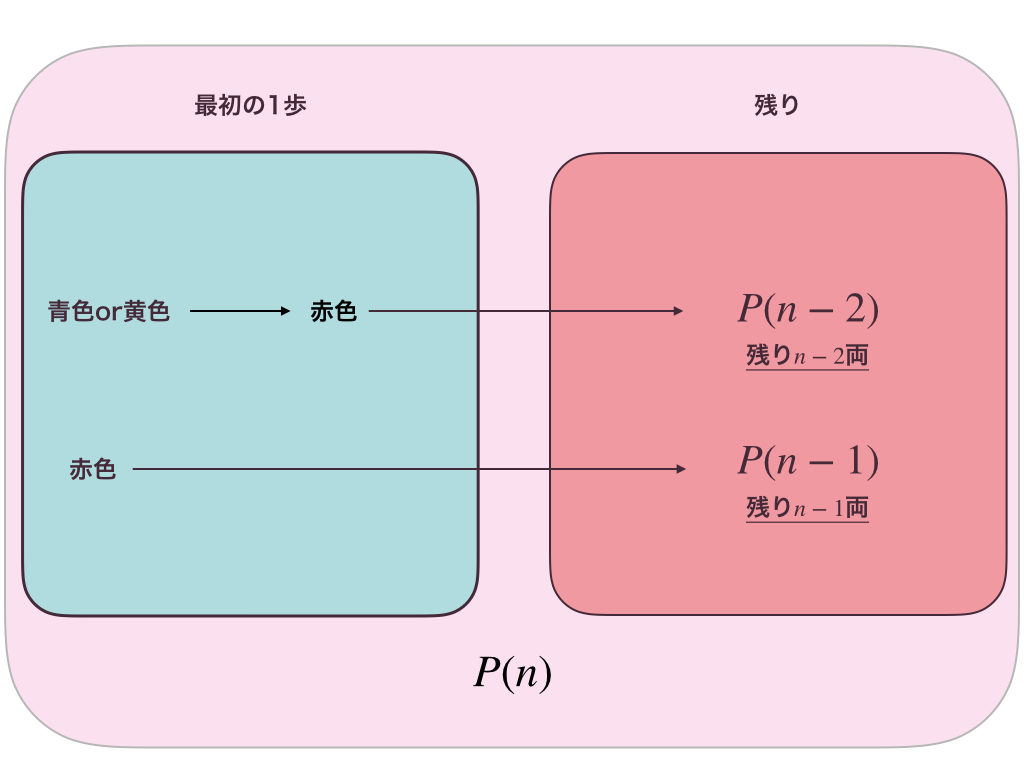
うん、完璧だね。これで、漸化式が立てられるよね。
そうだね。
$$P_{n} = P_{n-1} + 2P_{n-2}$$
かな?
正解! \(P_{n-2}\)の方は、黄色か青色の2パターンあるからね。それで、この形は三項間漸化式の典型例だから、解けるんだよ。ちなみに、この漸化式は、\(n\geq3\)で成り立つ漸化式だから、解いたあとで、\(n=2\)の時の確認が必要だよ。そのことを頭に入れておいて、解きやすくするために、ちょっと変形して
$$P_{n+2} = P_{n+1} + 2P_{n}$$
としておこっか。ようこちゃん、解ける?
特性方程式を作って、解を求めて変形する方法だね。特性方程式は
$$x^2 = x + 2$$
で、\(x=2, -1\)だから、2通りの式ができるね。
$$P_{n+2}-2P_{n+1} = -1(P_{n+1}-2P_{n})$$
$$P_{n+2}+P_{n+1} = 2(P_{n+1}+P_{n})$$
ここで、\(P(1) = 3, P(2) = 5, P(3) = 11\)ということを使って、上側 を解いて
$$P_{n+1}-2P_{n} = (-1)^{n-1}(P_{2}-2P_{1}) = (-1)^{n}$$
下側を解いて、
$$P_{n+1}+P_{n} = 2^{n-1}(P_{2}+P_{1}) = 2^{n+2}$$
あとは、\(P_{n+1}\)を消去すればいいんだね。
ウンウン、じゃあ答えは?
$$P_{n} = \frac{2^{n+2}-(-1)^{n}}{3}$$
かな。え〜と、それで、\(n=2\)の時の確認が必要なんだよね?
式に代入すると、5通りで、実際に調べても5通りだから、この式は\(n\geq2\)で成り立つ式だね!
すばらしい! ようこちゃん。もう、心配ない?
まだまだ! 次はないの?
いいねぇ。じゃあ、次はこれ。
1994年 第5問 赤い札を持っているのは誰?
問題
A, B, Cの3人が色のついた札を1枚ずつ持っている。はじめに、A, B, Cの持っている札の色はそれぞれ、赤、白、青である。Aがさいころを投げて、3の倍数の目が出たら、AはBと持っている札を交換し、その他の目が出たらAはCと札を交換する。この試行を\(n\)回繰り返した後に、赤い札をA, B, Cが持っている確率を\(a_{n}, b_{n}, c_{n}\)とする。
(1) \(n\geq2\)のとき、\(a_{n}, b_{n}, c_{n}\)を\(a_{n-1}, b_{n-1}, c_{n-1}\)で表せ。
(2) \(a_{n}\)を求めよ。
この問題が典型的な「縛り」だね。あまりに露骨だから、漸化式を立てることそのものが問題になっちゃってるよ。
ようやく、最後の一歩で場合分け、ていう問題だね。今まで通り、図を書いて調べてみよっか。
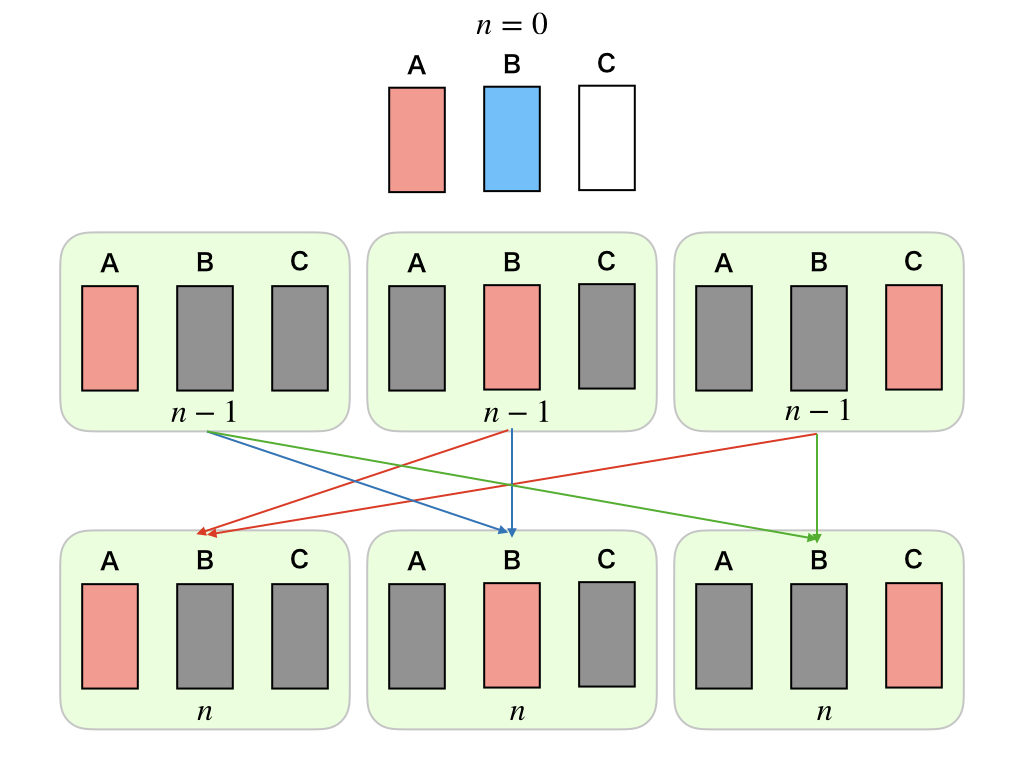
ようやく出たね。\(n-1\)回目までの試行を\(a_{n}\)なんてまとめちゃうパターン。今回は、\(n-1\)回目までが3通りあるから、ようこちゃんが書いた図みたいになるんだね。
この図から、\(a_{n}, b_{n}, c_{n}\)と\(a_{n-1}, b_{n-1}, c_{n-1}\)の関係を読み取ってみるね。問題の条件から、
1. AとBの札のスイッチは\(\frac{1}{3}\)
2. AとCの札のスイッチは\(\frac{2}{3}\)
だね。そうすると
$$a_{n} = \frac{1}{3}b_{n-1}+\frac{2}{3}c_{n-1}$$
$$b_{n} = \frac{1}{3}a_{n-1}+\frac{2}{3}b_{n-1}$$
$$c_{n} = \frac{2}{3}a_{n-1}+\frac{1}{3}c_{n-1}$$
かな。
ん〜、バッチリ! ちなみに、この式って、\(n=1\)でも成り立つことだよね。これって結構重要な確認なんだよ。もし、\(n\geq 2\)以上でしか成り立たない漸化式だったら、最後に\(n=1\)でもいいかどうか確認しなきゃならないからね。じゃあ、これ解こうか。
でも、ちょっと複雑だなぁ。これどうやって解くの?
一見複雑そうに見えるけど、要は、\(a_{n}\)の式の中から、\(b_{n}\)とか\(c_{n}\)とかを\(a_{n}\)の式で表せればいいんだよね。でも、このままだとちょっと大変かな。もう一つ式を作りたいなぁ。
もう一つ? ある?
こういう複数の文字が漸化式に現れた時に有効なんだけど、\(a_{n}, b_{n}, c_{n}\)全部足すとどうなる?
あっ、そうか、全部足すと、そりゃ、1だよね。
うん、だからさ、
$$a_{n}+b_{n}+c_{n}=1$$
になるんだよ。これで、文字を減らしていくんだ。
じゃあ、これで、\(a_{n}\)の式から\(b_{n}\)を消してみようかな。そうすると
$$3a_{n} = 1-a_{n-1}+c_{n-1}$$
$$c_{n-1} = 3a_{n}+a_{n-1}-1$$
$$c_{n} = 3a_{n+1}+a_{n}-1$$
だから、、、これを\(c_{n}\)の式に代入すれば、\(a_{n}\)だけになるね。結果は
\(a_{n+1} = \frac{1}{3}a_{n-1}+\frac{2}{9}\)だ!
正解だよ。ちょっとわかりやすくして、
$$a_{n+2} = \frac{1}{3}a_{n}+\frac{2}{9}$$
としておこっか。1個飛ばしの漸化式、ようこちゃん、解ける?
1個飛ばしは「偶奇に分けよ」
え? なにそれ?
いや、別になんでもないんだけど。とにかく、\(n\)を偶数、奇数に分ける必要があるね。まずは偶数の場合。\(n = 2k\)(\(k\)は自然数)とおくよ。
$$a_{2(k+1)} = \frac{1}{3}a_{2k}+\frac{2}{9}$$
この形は特性方程式で\(\alpha\)を求めればいいね。
$$\alpha = \frac{1}{3}\alpha + \frac{2}{9}$$
から\(\alpha = \frac{1}{3}\)だとわかるから、
$$a_{2(k+1)}-\frac{1}{3} = \frac{1}{3}\left( a_{2k} – \frac{1}{3}\right)$$
と変形できるね。\(a_{1} = 0, a_{2} = \frac{5}{9}\)を使うと、
$$a_{2k} – \frac{1}{3} = \left(\frac{1}{3}\right)^{k-1}\cdot\frac{2}{9} $$
$$a_{2k} = \frac{1}{3} + \frac{2}{3^{k+1}}$$
うん、それでいいと思うけど、\(k = \frac{n}{2}\)として
$$a_{n} = \frac{1}{3} + \frac{2}{3^{\frac{n}{2}+1}}$$
とした方がいいかな。それで、\(n\)は偶数と但し書きね。
おっけい。じゃあ、次は奇数ね。奇数はn=2k-1とおくけど、特性方程式の解は同じだから、結局
$$a_{2(k+1)-1}-\frac{1}{3} = \frac{1}{3}\left( a_{2k-1} – \frac{1}{3}\right)$$
まではほとんど同じだね。違うのは、初項だけだから、
$$a_{2k-1} – \frac{1}{3} = \left(\frac{1}{3}\right)^{k-1}\cdot\left(-\frac{1}{3} \right)$$
となって、
$$a_{2k-1} = \frac{1}{3}-\left(\frac{1}{3}\right)^{k}$$
今回は、\(k = \frac{n+1}{2}\)を使って
$$a_{n} = \frac{1}{3}-\left(\frac{1}{3}\right)^{\frac{n+1}{2}}$$
ただし、\(n\)は奇数
どうだ!
惚れ惚れするね、ようこちゃん。じゃあ、最後の問題。これはちょっと厄介かもよ。でも、解けたら、すごくスッキリするんだ。
2012年 第6問 複雑そうに見える根号式が絶妙のバランス! 挑戦する価値ある難問
問題
さいころを\(n\)回投げて出た目を順に\(X_{1}, X_{2}, \cdots, X_{n}\)とする。さらに
$$Y_{1} = X_{1},\ Y_{k} = X_{k} + \frac{1}{Y_{k-1}}\ (k=2, \cdots, n)$$
によって、\(Y_{1}, Y_{2}, \cdots, Y_{n}\)を定める。
$$\frac{1+\sqrt{3}}{2}\leq Y_{n}\leq 1+\sqrt{3}$$
となる確率\(p_{n}\)を求めよ。
??????
え〜と、どうなってるのかな? これ。
落ち着いて、ようこちゃん。落ち着いて、まずどんなことをやっているのか、イメージしながら、考えてみるんだよ。
まず、さいころを振るでしょ。それで目が出て、それを\(X\)と置く。そのあと、\(Y\)を計算して、\(Y\)の値の範囲を調べる。それで、またさいころを振る。この繰り返しだね。
そうでしょ。そんな複雑なことしていないんだよ。それと、あたしがずっと言ってきたこと、あったでしょ。
え〜と、うん。縛りを探せ、ってことでしょ。今回こそ、露骨な縛りがあるよ。
$$Y_{k} = X_{k} + \frac{1}{Y_{k-1}}$$
っていう漸化式だね。
そうなんだよ。だから、この問題を最終問題に選んだんだけどね。こんな縛りがあったら、確率漸化式として解くっきゃないでしょ。
じゃあ、次は最初の一歩か最後の一歩か、どっちかを考えなきゃね。私流の方法は、最後の一歩で試してダメだったら、最初の一歩に持っていくって方法だけど、今回は、\(n-1\)回目までを\(p_{n-1}\)とおいてしまって大丈夫そうだね。だから、最後の一歩で場合分けだ!
……。
え? 違うの?
これ以上は、あたしはノーヒント。ようこちゃん、一人で頑張ってよ。
あ、いつもの仕返しだね〜。おっけい。じゃあ、やってみるよ。とりあえず、\(n-1\)回目までに、\(Y_{n}\)が条件を満たしている場合と、満たしていない場合の2通りがあって、満たしていない場合は、さらに、不等式の下側にある場合と上側にある場合で、合計3通りあるから、一つずつ図を書いてみるよ。
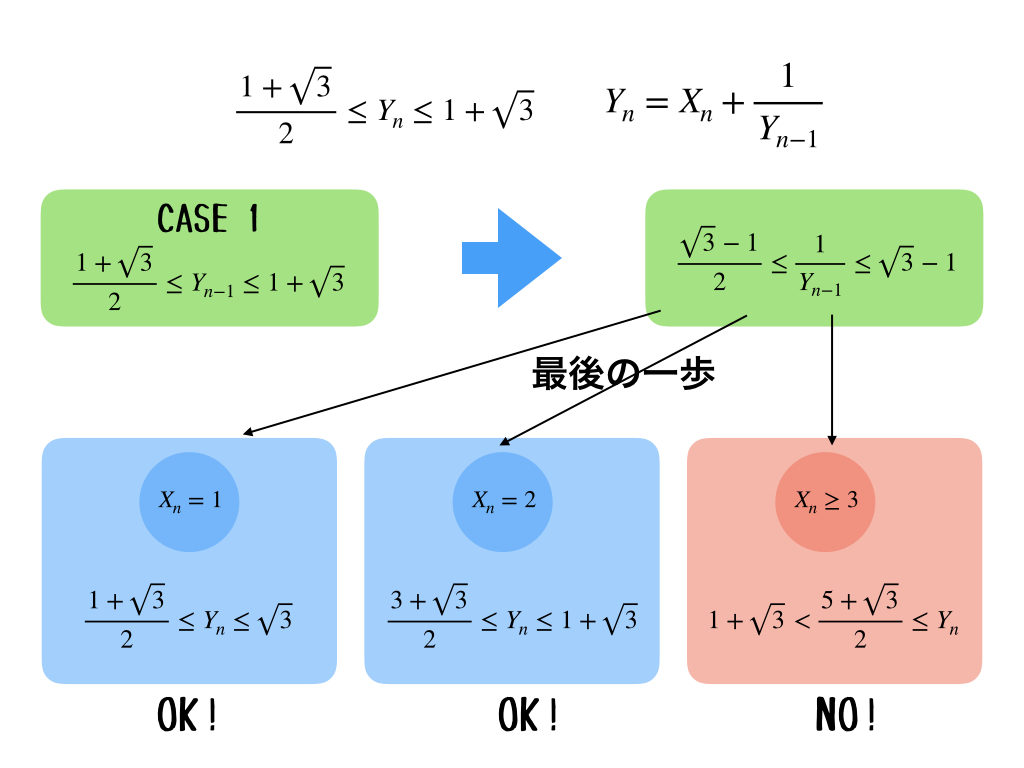
ゆっくり進めていくね。まず、\(Y_{n-1}\)が条件を満たしているとき。この時に、\(Y_{n}\)がさらに条件を満たすような\(X_{n}\)が何通りあるかを考えればいいわけだから、\(Y_{n} = X_{n}+\frac{1}{Y_{n-1}}\)を使って計算すればいいよね。一つずつ代入していけば良さそうだけど、\(X_{n}=3\)を代入したとき、\(Y_{n}\)の不等式の左の値が\(1+\sqrt{3}\)を超えちゃうから、それ以上の\(X_{n}\)を入れてもダメだね。だから、この場合は\(X_{n}=1, 2\)の2通りあるってことか。
ふむふむ。
じゃあ、次は、\(Y_{n-1}\)が条件を満たしていないとき。特に、不等式の左側にある場合を考えるよ。
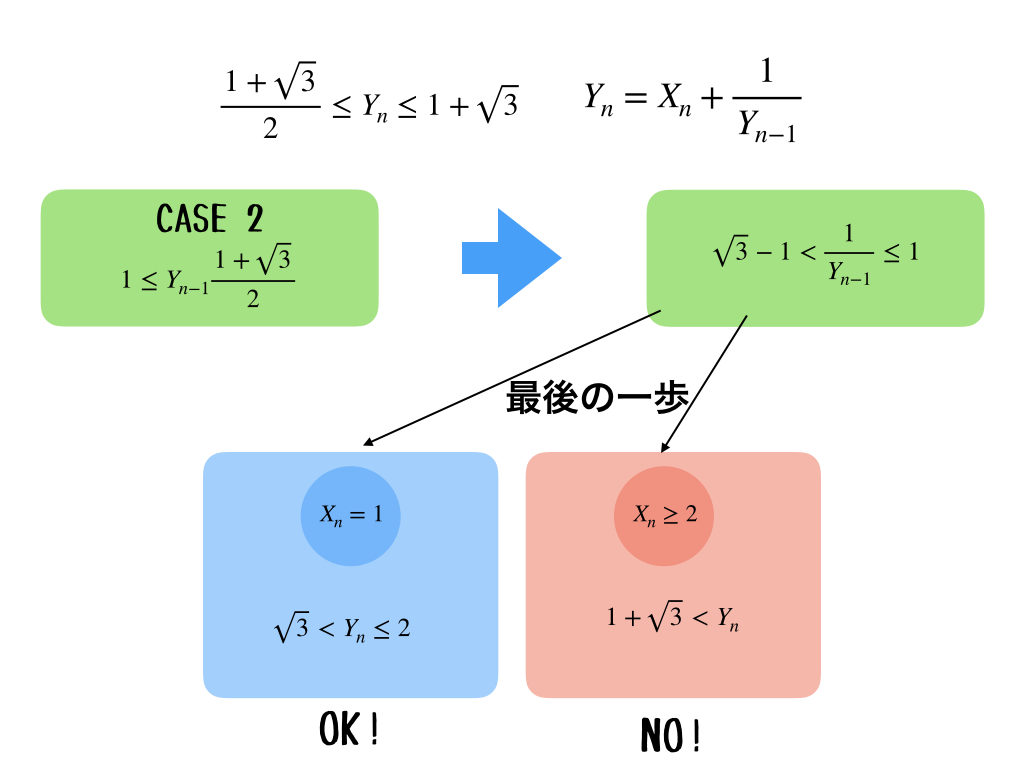
\(1\leq Y_{n-1}\)はどこから来たの?
あ、それは、\(Y_{n} = X_{n}+\frac{1}{Y_{n-1}}\)の式からだよ。それと、\(X_{1}=Y_{1}\)だね。\(X_{n}\)、つまり\(n\)回目のさいころの出目の最小値が1だからね。この場合は、\(X_{n}\geq 2\)の時にはもう、\(Y_{n}\)の条件を満たさないことがわかる。だから、\(X_{n}=1\)の1通りしかないね。
いいねぇ、ようこちゃん。
じゃあ、最後のパターンね。
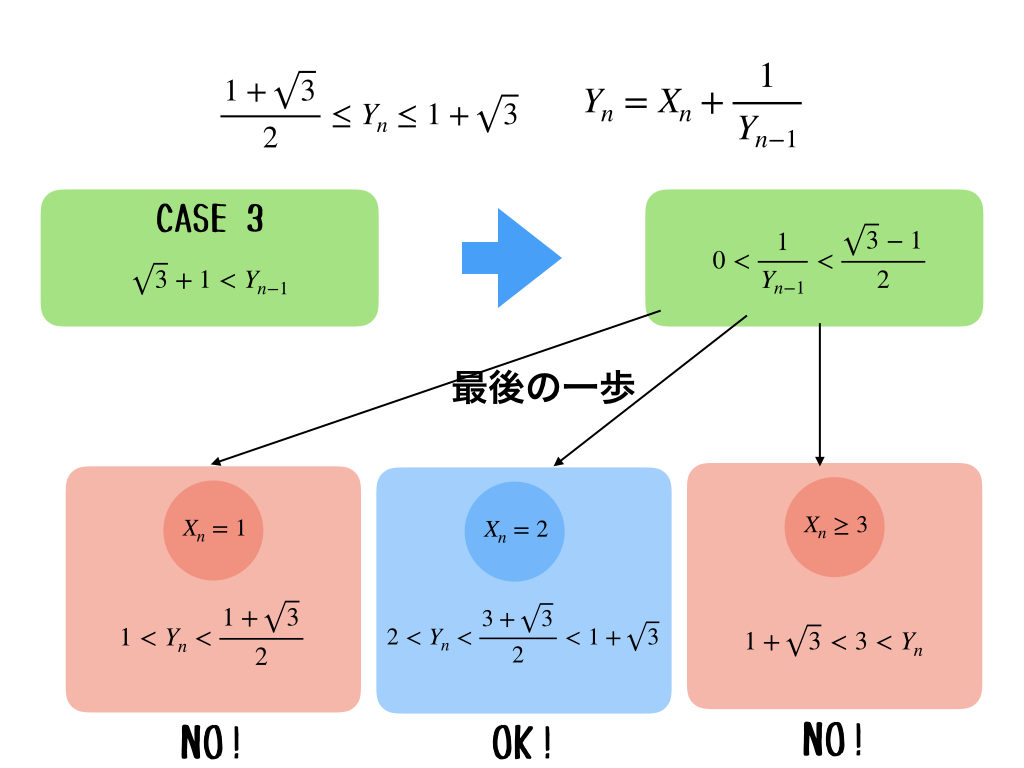
\(0<\frac{1}{Y_{n-1}}\)の部分は、、、まぁ、いいか。
うん。まぁ、式の形から、負になることはないよね。この場合は、上の図に書いた通り、\(X_{2} = 2\)のときだけOKだね。これは嬉しい結果よね。だって、\(Y_{n}\)が条件を満たしていないときは、両方とも\(X_{n}\)が1通りしかないんだもん。
じゃあ、今までの結果をまとめてみようよ!
2. \(Y_{n-1}\)が条件を満たしていないとき、\(Y_{n}\)が条件を満たすには、\(Y_{n}\)が不等式の下側にいるとき\(X_{n} = 1\)、または不等式の上側にいるとき、\(X_{n} = 2\)のそれぞれ1通りが適する。
\(Y_{n-1}\)が条件を満たす確率は\(p_{n-1}\)と置けるし、\(Y_{n-1}\)が条件を満たさない確率は\(1-p_{n-1}\)と置けるね。あ! これなら、すぐに漸化式を作れるんだ。
そうなんだよ! もし、2の方、\(Y_{n-1}\)が不等式の下側と上側にいるときで、\(X_{n}\)の許される数が違ったら、簡単にはいかないんだ。複雑に見えるけど、\(Y_{n}\)の満たす条件式が絶妙なんだよね。
そうだね。今だったら
$$p_{n} = \frac{1}{3}p_{n-1} + \frac{1}{6}(1-p_{n-1}) = \frac{1}{6}p_{n-1}+\frac{1}{6}$$
ってわかるもんね! ちなみに、\(p_{1} = \frac{1}{6}\)だね。
$$p_{n+1} = \frac{1}{6}p_{n}+\frac{1}{6}$$
としてもいいんだよね。
あと一歩だね、ようこちゃん。
うん。あとは特性方程式を解いて、計算だ。特性方程式を解いて変形すると、
$$p_{n+1}-\frac{1}{5} = \frac{1}{6}\left(p_{n} – \frac{1}{5}\right)$$
だから、これを解いて、
$$p_{n} = \frac{1}{5} – \frac{1}{5}\left(\frac{1}{6}\right)^{n} = \frac{1}{5}\left( 1-\frac{1}{6^{n}} \right)$$
かな?
すご〜い。ようこちゃん、この問題もできたじゃん!
、、、と言いたいところだけど、1点だけ、注意が必要!
最後の漸化式、
$$p_{n} = \frac{1}{3}p_{n-1} + \frac{1}{6}(1-p_{n-1}) = \frac{1}{6}p_{n-1}+\frac{1}{6}$$
は、\(n\geq2\)の時にしか成り立たない式だよね? その場合、\(n=1\)の時も成り立っていることを確かめておかないといけないんだよ。今は、\(p_{1} = \frac{1}{6}\)で、出てきた式に\(n=1\)を代入しても\(\frac{1}{6}\)になるから大丈夫、みたいなことを書いておかないとね。
あ、そうか。勉強になります!
でも、重要なところはちゃんとできてるし、さすが、ようこちゃん!
そんなことないよ〜。まみが教えてくれたことをそのまま当てはめてみただけだからね。わかりやすかったよ!
え、そうかな。へへ。
最後は、まみがまとめてよ。
OK! じゃあ、場合の数や確率を漸化式を立てて解く問題の、攻め方をまとめておくね。
(例)「隣り合う〜」「連続しない」「試行ごとに何かを交換する」「漸化式」
2. 漸化式が使えると思ったら、「最初の一歩」か「最後の一歩」で場合分け。手順としては、\(n-1\)回目までの試行を\(p_{n}\)とおいて、場合分けが容易にできそうなら、「最後の一歩」で場合分けして、それが難しいのなら「最初の一歩」で場合分けしてから、残りを\(p_{n-1}\)などを使って表す。
3. 2の漸化式を解く。この時、\(n=1\)などの初期条件に注意。漸化式は\(n\geq2\)など、初期条件より大きい値からしか成立しないこともあるので、最後に確認が必要なことがある。
特に、2が漸化式の魅力だね。漸化式を使わないなら、\(n\)回分の試行全部を考えて計算しなくちゃいけないのに、漸化式を使えるなら、たった1歩か2歩だけ考えればいいんだから。
あとは、漸化式を解くパターンは一通り身につけていないとダメだね。せっかく漸化式ができたのに、解けませんでした、じゃ悲しいもんね。
そうそう! 確率や場合の数は「数列」とものすごく相性がいいから、大学入試なんかで確率の勉強をするときは、「数列」をしっかりやっとかないと痛い目をみるかも。
でも、まみのおかげで解き方のコツを掴んだ気がする。ありがと!
数学は任せてよ。その代わり、物理はお願いね。



コメント