質問リクエストにおいて、以下の問題をいただきました。主に電動機に関する問題なので、はじめに電動機に関する簡単な紹介を行ってから問題に取り組みたいと思います。
2. 直巻電動機の端子電流が 10.0[A]のとき,回転速度が 1000[min-1],トル クが 40.0[N・m]で運転している。電流が 20.0[A]になったときの回転速度とトル クを求めよ。ただし,磁束は電流に比例,回転速度は電流に反比例,トルクは電流の 2 乗 に比例するものとする。
3. ある他励電動機に負荷をつなげて定格電圧,定格電流,定格回転速度 (1500[min-1])で運転した。負荷を切り離したところ回転速度が 1575[min-1] になった。この他励電動機の速度変動率を求めよ。
4. 面積 1.0[km2]に降る 1 時間あたり 60[mm]の降雨を貯水池に集め,これ を 5 台の同一仕様のポンプで均等に分担し,全揚程 12[m]を揚水して河川に排 水する場合,各ポンプの理論動力と,駆動用電動機の所要出力を求めよ。ただ し,1 時間の排水量は降雨量に等しく,ポンプの効率は 0.8,設計製作上の余 裕係数は 1.2 とする。
5. ビルの空気調和機用に送風機を利用して,風量 600[m3/min],風圧 1500[Pa] の空気を送出する場合,この送風機用電動機の所要出力はいくらか。ただし, 送風機の効率は 0.6,余裕係数は 1.2 とする。
電動機の仕組み
電動機の一般的な説明は「電気エネルギー」を「運動エネルギー」に変換する装置ということができます。この意味では、電動機は発電機と対となる電気器具だといえます。電動機の原理はローレンツ力であり、導線に流れる電流が作る磁界と外界のコイルが持つ磁界の相互作用により生じる力を、動力の源にしています。その力の向きは、フレミングの左手の法則で理解することができます。
直流電動機の簡単な構造を示したものが以下の図です。
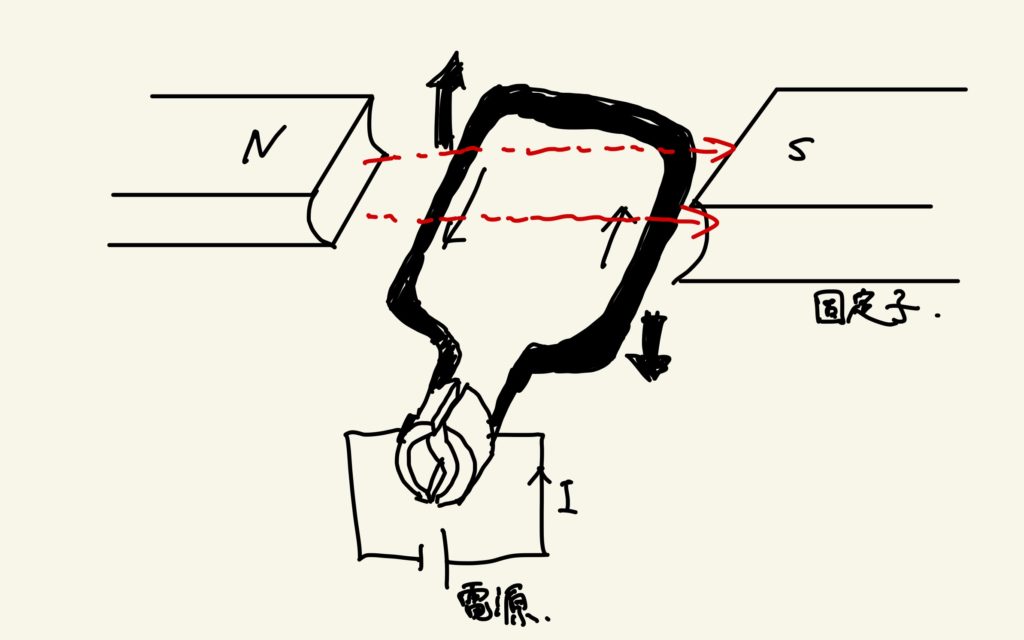
ここで、固定子と書いてある部分で磁力を発生させています。黒い棒が導体部分で、ここに直流電源から電流を流すことで磁界を発生させます。このように発生した2種類の磁力の相互作用により、導体部分を動かす力(ローレンツ力)が生まれています。電動機では以下の言葉がよく用いられます。
- 界磁:固定子(と回転子)に発生する磁力
- 界磁電流:固定子に流れる電流(固定子が電磁石である場合など)
- 電機子:界磁と相互作用して力を生み出す部分(上の図の導体部分)
- 電機子電流:電機子に流れる電流
- トルク:電機子に働く回転モーメント(回転させるために必要な力)
トルクは大学の物理(剛体の力学)で詳しく学びますが、高校物理でも「力のモーメト」という名前で登場します。トルクに関するわかりやすい説明は、こちらのサイトhttp://www.energychord.com/children/energy/motor/dc/contents/dc_aamain.htmlを参照されると良いかと思います。簡単な言葉で言ってしまうと、剛体(大きさのある物体)を回転させるための力となります。また、電動機に発生するトルクについて重要なことはその大きさが、「電機子に流れる電流の大きさ」と「1極あたりの電機子に発生する磁束」の両方に比例する物理量である、ということです。
直流電動機の種類
発電機の時にも紹介したように、直流電動機には、自励式(直巻・分巻)と他励式があります。直巻は電動機と界磁を直列につないだもので、分巻は電動機と界磁を並列につないだものを言います。それぞれの等価回路を以下に示します。
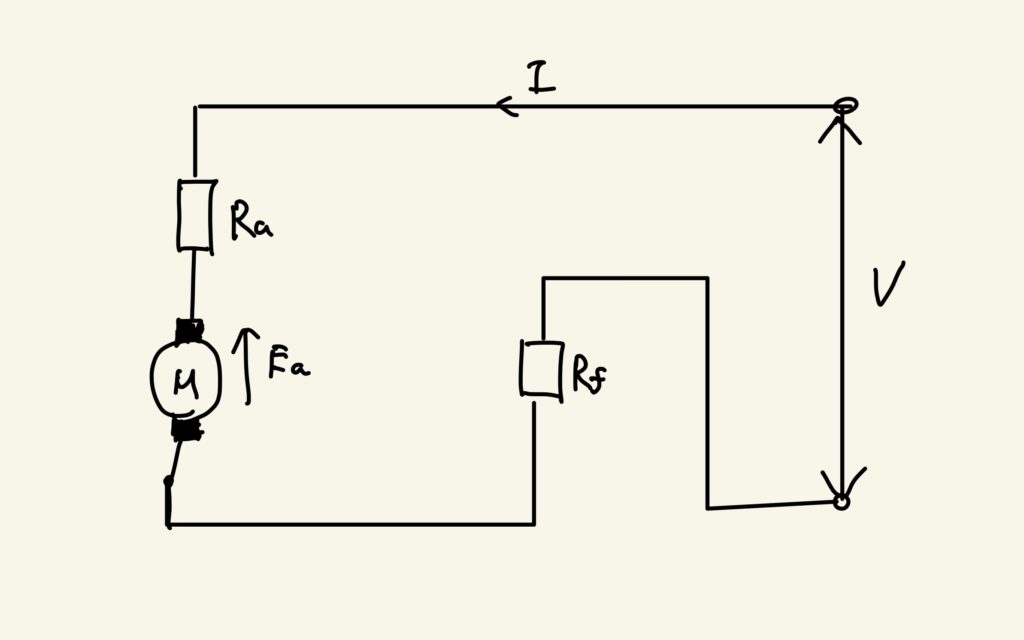
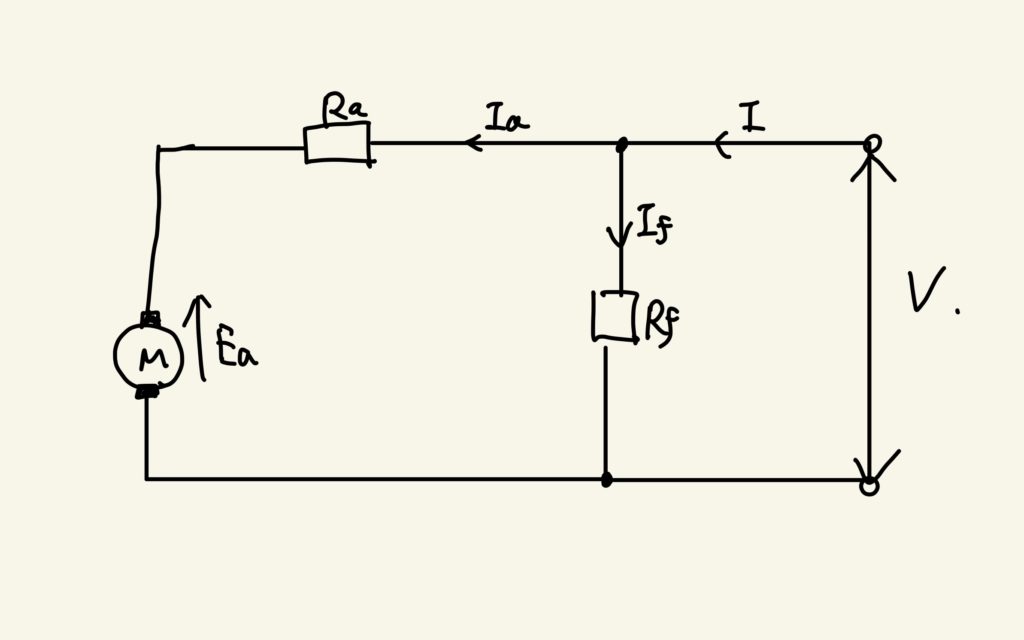
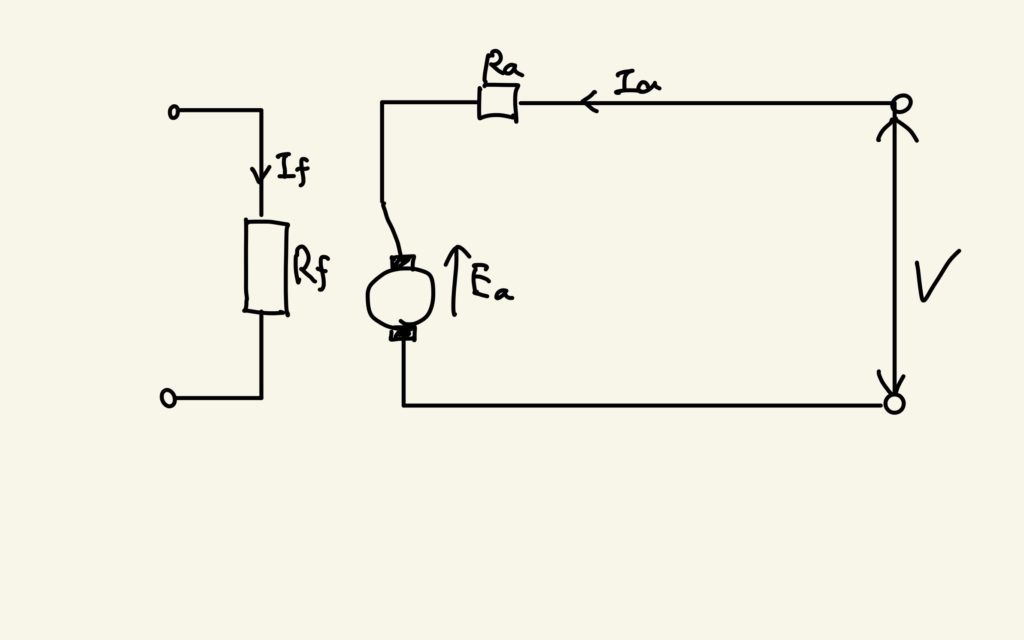
このように、回路の問題を解くときは、各電動機の等価回路を使って解くのが最も解きやすい方法かと思います。
直流電動機の具体的な問題
ここからはいただいた質問の回答を行っていこうと思います。
問題1 直流分巻電動機
電機子抵抗 0.25[Ω],界磁抵抗 50.0[Ω]の分 巻電動機の端子に直流電圧 100[V]を印加したところ端子電流が 15.0[A],回転 速度が 1200[min-1]になった。このときの界磁電流と電機子電流,逆起電力,入力と出力,トルクと効率を求めよ。
直流分巻電動機に、問題文の各値を代入していくと以下の図のように書けます。
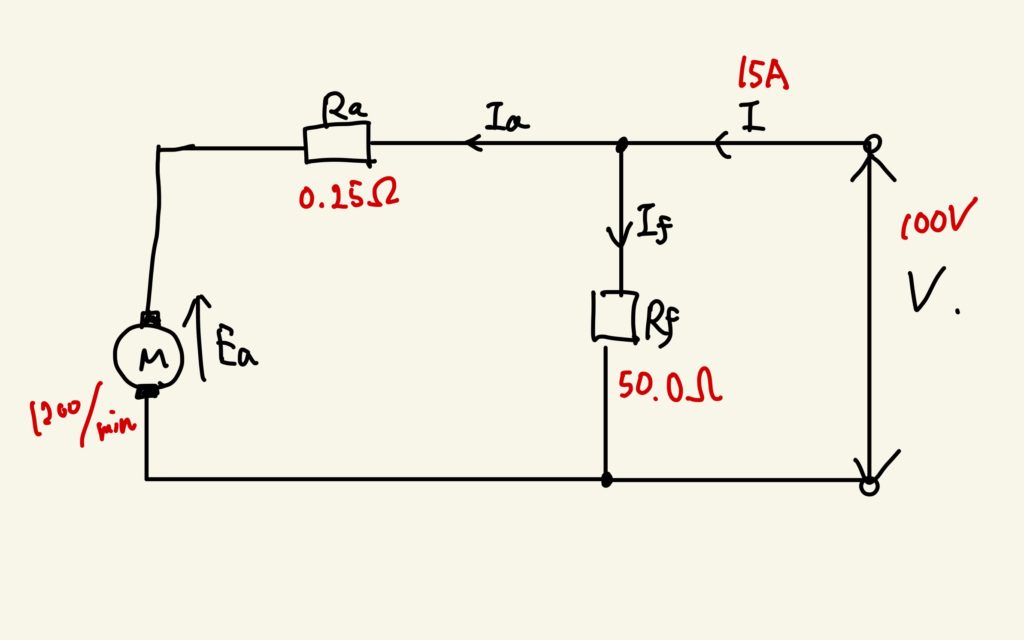
界磁電流と電機子電流については、次のように計算できます。
まず、電動機と界磁部分が並列に繋がっているので、それぞれに100Vの電圧がかかります。界磁部分に100Vがかかるとオームの法則より、\(100/50 = 2.0 A\)と求められます。このことから端子電流から界磁電流を引くと、電機子電流が求められるので、電機子電流は13.0Aと求められます。電動機について、逆起電力と端子電力との関係は
$$E_{a} = V – R_{a}I_{a}$$
となっているので、いま求めたものを用いると\(E_{a} = 100 – 0.25*13.0 = 96.5 V\)です。
次に、入力と出力および効率を求めます。効率は発電機の時と同様に計算することができます。電動機の出力は\(P=E_{a}\times I_{a}\)と求めることができるので\(1254.5 (W)\)であり、これに損失を加えたものが入力となります。ここでの損失は界磁および電機子での抵抗熱の和であるから\(50\times2\times2 + 0.25\times13\times13 = 242.25 (W)\)です。ゆえに効率は
$$\eta = \frac{1254.5}{1254.5+242.25} \simeq 83.81$$
よって、83.8%と計算できます。
最後にトルクを求めます。トルクを求める方法はたくさんありますが、電動機の場合、回転速度が与えられているので、回転速度とトルクの関係を知ることが必要です。今、回転速度の単位が[/min]であるので、回転速度とトルクの関係は次式で与えられます。
$$P = \frac{2\pi nT}{60}$$
です。\(P\)は電動機の出力、\(n\)は回転速度で\(T\)はトルクです。この式から
$$T = \frac{60\times P}{2\pi n}$$
とかけるので各値を代入すると\(T \simeq 9.982\)であり、有効数字3けたで求めると9.98(\(N\cdot m\))となります。
問題2 直流直巻電動機
直巻電動機の端子電流が 10.0[A]のとき,回転速度が 1000[/min],トルクが 40.0[N・m]で運転している。電流が 20.0[A]になったときの回転速度とトルクを求めよ。ただし,磁束は電流に比例,回転速度は電流に反比例,トルクは電流の 2 乗 に比例するものとする。
問題文を見ると、回転速度は電流に反比例するとあります。これは回転速度(n(/min))の式が
$$n = k\frac{E}{\Phi}$$
とかけることから来ています。ここで、\(k_{1}\)は電機子によって決まる定数、\(\Phi\)は電機子を貫く磁束、\(E\)は誘導起電力です。電機子を貫く磁束は、界磁電流が2倍になると2倍になるという比例関係があります。よってその回転速度は1/2倍になるというわけです。今、直巻電動機を考えているため、端子電流と界磁電流、電機子電流は全て同じ値ですので、端子電流が2倍になれば界磁電流も電機子電流も2倍になります。以上より、回転速度は500[/min]となります。
次にトルクです。問題文によるとトルクは電流の2乗に比例するとあります。これはトルクの式が
$$T = k\Phi I_{a}$$
とかけるところから来ています。\(k_{2}\)は電機子によって決まる定数、\(\Phi\)は磁束、\(I_{a}\)は電機子に流れる電流を示します。磁束も電機子電流も、端子電流が2倍になると2倍になるので、今の場合トルクは端子電流の2乗に比例することになります(これは直巻に成り立つ性質で、分巻の場合はこのような関係でないことに注意)。今電流が2倍になったので、トルクは4倍になり、答えは160 [N・m]と計算できます。
問題3 他励電動機
速度変動率とは、発電機のところで紹介した電圧変動率と同じような定義がなされています。通常、以下の式で書くことができます。
$$\eta = \frac{N_{m}-N_{n}}{N_{n}}{N_{n}}$$
ここで\(N_{m}\)は無負荷での電動機の回転速度、\(N_{n}\)は定格運転時の電動機の回転速度です。この式に問題の条件を当てはめると
$$\eta = \frac{1575-1500}{1500} = 0.05$$
よって、速度変動率は5%と求められます。
ポンプの理論動力と所要出力
面積 1.0[km2]に降る 1 時間あたり 60[mm]の降雨を貯水池に集め,これ を 5 台の同一仕様のポンプで均等に分担し,全揚程 12[m]を揚水して河川に排 水する場合,各ポンプの理論動力と,駆動用電動機の所要出力を求めよ。ただ し,1 時間の排水量は降雨量に等しく,ポンプの効率は 0.8,設計製作上の余 裕係数は 1.2 とする。
ポンプの理論動力を決定するために必要な物理量は以下の通りです。
- \(g\) :重力加速度 [\(m/s^{2}\)]
- \(\rho\):吸い上げる物質(水など)の密度 [\(g/m^{3}\)]
- \(H\):吸い上げる揚程 [m]
- \(Q\):単位時間当たりに吐き出す流量 [\(m^{3}/s\)]
これらを用いるとポンプの理論動力(\(P_{w} (W)\))は
$$P_{w} = \rho g HQ$$
と求められます。また電動機の所要出力はこれに余裕係数(\(k\))・ポンプ効率(\(\eta\))を考慮して
$$P_{a} = \frac{kP_{w}}{\eta} (W)$$
と計算します。
問題文の条件より、\(\rho = 1\), \(H = 12\)とわかります。重力加速度は指定がなければ9.8を用いてよいでしょう。あとは単位時間当たりに吐き出す流量を求めます。これは問題文の指定では、排水量に相当します。排水量は降雨量に等しいことから、
$$\frac{1000\times1000\times0.06}{60\times60} = \frac{50}{3} [m^{3}/s]$$
となります。以上より必要な理論動力の合計は
$$9.8\times1\times12\times\frac{50}{3} = 1960 (W)$$
です。本問の場合、5台のポンプに均等に分担させるので各ポンプの理論動力はこれを5で割ったものだから、\(392 (W)\)です。
次に、所要出力を求めます。上で述べた公式を用いると
$$P_{a} = 1.2*392/0.8 = 588 (W)$$
と計算できます。
問題5 送風機の理論動力と所要出力
ビルの空気調和機用に送風機を利用して,風量 600[m3/min],風圧 1500[Pa] の空気を送出する場合,この送風機用電動機の所要出力はいくらか。ただし, 送風機の効率は 0.6,余裕係数は 1.2 とする。
先ほどと同じように送風機の理論動力を求めるために必要な物理量を列挙します。
- \(Q\):風量 (\(m^{3}/s\))
- \(H\):風圧 (Pa)
これらの物理量を用いると送風機の理論動力は
$$P_{w} = QH (W)$$
と求められます。先と同様に送風機の所要出力はこれに余裕係数(\(k\))・ポンプ効率(\(\eta\))を考慮して
$$P_{a} = \frac{kP_{w}}{\eta} (W)$$
と計算します。今の問題の条件を適用すると、求める送風機用電動機の所要出力は
$$P_{a} = \frac{1.2\times \frac{600}{60} \times 1500}{0.6} = 300000 (W) = 300 (kW)$$
と計算できます。
終わりに
間違いやご不明な点などございましたら、指摘していただけると私の勉強にもなります。よろしくお願いいたします。

コメント