さぁ、高校数学研究第2弾を始めるよ。
今日は、「ほとんど中学数学の知識だけで解く」ということをテーマに問題を集めてみました! 前回はいなかったけど、今回はえりかちゃんも参戦します。
あ、よろしくお願いします。
中学数学で解く、ってことは、「中学数学で解ける」問題を集めてくれたってことだよね。でも+αって、何のこと?
あ、それね、すぐ説明するよ。みうちゃんも頑張って。
今日は何問くらいやる?
8問くらいかな。時間があったらもっとやりたいけど。あ、みよちゃんも来てくれたんだね!
まぁ、言われたからね。
ありがと! じゃあ、まず、+αの部分を説明するね。計算や証明する過程で使う数学は中学数学で解けるものばかりだけど、高校に入ってすぐに習う、”実数”と”不等式”の証明だけ追加しておきたいんだ。この二つって中学数学でも何となく習うんだけど、高校に入ってようやく教科書にまとめられるようになる話だからね。ここでは、中学生でも理解できる話で、重要なところだけをまとめておくよ。本当は実数はもっと奥深い話なんだけどね。
例えば、
$$\frac{5}{6},\ \ 5,\ \ 0.5,\ \ 0.333333\cdots\cdots$$
などは有理数。
$$\pi, \sqrt{2}$$
などは無理数。
\(0.333333\cdots\cdots\)は例えば\(\frac{1}{3}\)のことを言っているんだよね。循環小数というもの。
そうだよ。割り切れる小数が分数で表せるというのは小学生でやるけど、割り切れない小数が実は分数で表せるというのは高校生で習うんだよね。でも、これも有理数だよ。実数で非常に重要な性質は次のものだね。
$$a^{2}\geq 0$$
これらって当たり前のように使っているけど、どっちも実数であることからくる性質だよね。高校生に入ると「虚数」というのを習うけど、「虚数」では上の常識が覆るから注意しないといけないよ。
さて、実数の話はこんなとこ。次は不等式の証明だけど、これはすごく簡単に済ませるよ。中学数学でも不等式は習っているよね。高校生に入ると、等式を証明するだけではなくて、不等式を証明せよ、っていう問題も登場してくる。
$$A-B\geq 0$$
を示すことである。
他にも色々あるんだけど、これだけ知っておけば、今日は大丈夫。みんなも、この方法で解くことを考えてみてね。じゃあ、1問目は、問題としては全然難しくないと思うけど、確率論で非常に重要な考え方に関する問題をやるよ。
1980年第4問 6回振ったら必ず1が出る?
「サイコロを6回ふることにする。\(m=1, 2, 3, 4, 5, 6\)のおのおのについて、\(m\)回目に1の目が出る確率は\(\frac{1}{6}\)である。したがって、6回のうちに少なくとも1回1の目が出る確率は
$$\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6} =1$$
すなわち、サイコロを6回ふれば少なくとも1回は1の目が出る。」
A君の考えは正しいかどうかをいえ。もし正しくないならば、誤りの原因を、なるべく簡潔に指摘せよ。
面白い問題でしょ。誰もが一度は考えるようなことだよね。
これは私でもわかる! やってもいい?
どうぞ、どうぞ。
まず、A君の考え方は誤り、だよね。原因っていうか、サイコロを6回ふって少なくとも1回は1の目が出る確率というのは、サイコロを6回ふったときに、常に1から5が出る確率を1から引けばいいんだから
$$1-\left(\frac{5}{6}\right)^{6}$$
となって、1にはならない。そこの計算が違うから、サイコロを6回振っても1の目が必ず出るとは限らない。
うん、そうだね! A君の最大の誤りは足し算をしてしまったということなんだ。サイコロを振る試行というのは、数学的には1回1回が独立な試行だよね。独立な試行を繰り返す時は、「足し算」ではなくて「かけ算」で計算しなければならなかったというのが誤りの原因だね。
あれ? でも、確率を足し算で求めることができることもあったよね?
うん。でも、それは全然違う場合だよ。確率の加法定理っていうんだけど、1回の試行において、互いに共通部分のない2つの事象(イベント)の和は、足し算で求められるっていうものだったね。具体的には。
「1個のサイコロを投げて、3の倍数が出る確率と5の倍数が出る確率を求めよ」
っていう問題があったとしたら
$$\frac{2}{6} + \frac{1}{6} = \frac{1}{2}$$
って求められるよね。ここで、3の倍数が出るイベントと5の倍数が出るイベントは共通部分がないから、そのまま足し算できるというのが加法定理が教えてくれるところだよ。
今の問題だと、6回サイコロを投げるっていうことを「1回の試行」だという風に考えるとしても、たとえば「1回目に1の目が出るイベント」「2回目に1の目が出るイベント」というのは、もうすでに共通部分が発生しちゃってるもんね。共通部分があるときは単に足し算じゃなくて、「共通部分を引く」ってことが必要だよね。
あ、ようこちゃん、出番!
え? な、なに? 図をかけってこと?
ベン図、ベン図。
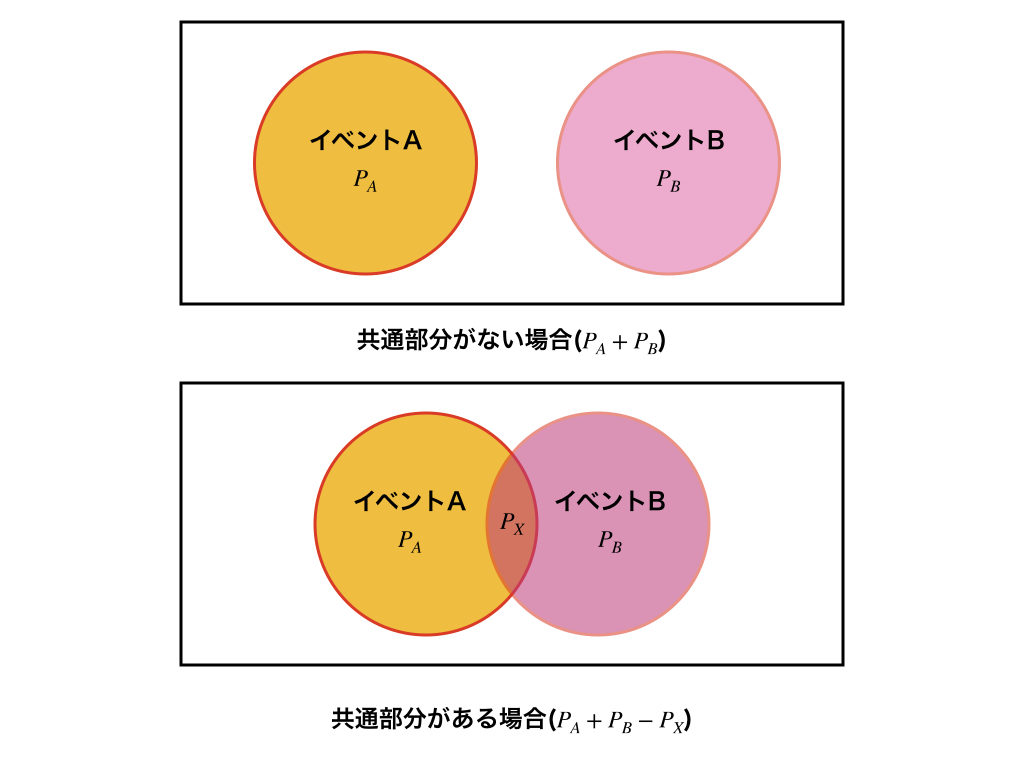
そうそう、これこれ。えりちゃんのいうとおり、共通部分がある時は引かないといけない。単なる足し算じゃダメなんだね。だから、A君の方法は間違っていて、みうちゃんのように計算しないとダメだったんだ。ちなみに、みうちゃん。それ、計算するとだいたい何%になる?
え? これ、計算するの?
そうだよ! 頑張って!
え〜と、みよちゃん、ヘルプ!
それくらい自分で計算しなよ。
き、きびしい。え〜と、じゃあまず分数で考えると。。。。。。
$$1-\frac{15625}{46656} = \frac{31031}{46656}$$
え〜と、次に割り算をして、だから、だいたい66%くらいかな。
意外と低いんだね。
そう、意外と低いんだよ。A君のように直感的に考えちゃうと、まるで100%見たく思えるけど、実際は全然違うんだね。
確かに、問題としては簡単だけど、確率の考え方を再認識する上ではとても重要かも。
そうでしょ! じゃあ、次はちょっと頭の体操が絡む問題。
1975年第1問 リーグ戦の結末
さぁ、これは計算が全くいらない証明問題だけど、どうする?
わたしが、やってみてもいいかな?
お、えりちゃん、どうぞどうぞ。
う〜ん、論理的な問題だよね。同順位のチームがなかったってことは、1位のチームが必ずいて、下位のチームに必ず勝っているということは、そのチームは全勝しているはずなんだね。だったら、まずこれを示したい。
1位のチームがいることは明らかだから、そのチームが仮に1回どこかのチームに負けているとする。そうすると、1位のチームの勝ち数は\(n-2\)だから2位以下のチームが同順位にならないためには、それぞれ0勝から\(n-3\)勝のチームが1組ずつあることになる。0勝から\(n-3\)勝までの割り当て方は\(n-2\)通りで、2位以下のチームの合計数は\(n-1\)チーム。ということはどう頑張っても、少なくとも2チームは勝ち星が被ってしまう。これは問題文の条件に合わない。だから、1位のチームは全勝していないとだめ。
同様に、2位のチームが1位のチーム以外に負けているとすると、3位以下のチームの勝ち数はそれぞれ、0勝から\(n-4\)勝で被っちゃいけないけど、これの割り当て方は\(n-3\)通り。3位以下のチームの合計数は\(n-2\)チームで、やっぱり勝ち星が被ってしまう。だから、2位のチームは1位のチーム以外に全勝していることになる。3位以下のチームにも同様のことが成り立つから、それぞれのチームは、下位のチームには全勝している。
これでどうかな?
うん、正解だと思うよ。えりちゃんは言葉にはしていないけど、数学的には「背理法」と「鳩の巣原理」というのを用いているね。
背理法は、「ある命題が真だと仮定した時に矛盾が生じたならその命題は偽」ということを利用した証明方法だよね。
うん。数学における「命題」というのは単なる文章じゃなくて、真か偽かが必ず決まる文のことだからね。真でないなら、必ず偽となる。
じゃあ、鳩の巣原理って?
鳩の巣原理というのは、例えば、鳩の巣が6つだけあるとするでしょ。そこに7羽の鳩を入れようと思ったら、少なくとも1つの巣には鳩を2羽入れないといけない、という原理のことだよ。
え〜、そんなの当たり前じゃん! なんで「鳩の巣原理!」なんて、偉そうな名前がついているの?
みう、実は、この原理は突拍子もないことを証明することだってできるんだよ。例えば、今現在日本に住んでいる人たちの中には、年を除いて、秒単位で同じ日に生まれた人が少なくとも1組は存在するってことを証明できるよ。秒単位っていうのは、例えば、3/18/14:43:23っていうことね。
え? そうなの?
うん。これは、一瞬だけだと、当たり前には思えないよね。誕生日が同じっていいうのはよくあることだけど、秒単位まで同じ人たちがいるというのは信じ難いかも。でも鳩の巣原理を使えば、いちいち聞き込みしなくなって、証明できる。みう、1年間って何秒ある?
1年間? え〜と、\(60\times60\times24\times365\)だから、って、またこんな計算!? \(31536000\)かな、多分。
うん、まぁだいたいそんなところ。閏年とかあったらずれるけど。それで日本の人口は?
だいたい1億人くらいじゃない?
ほら! 鳩の巣原理が使える。1億人に、この3000万くらいの時間を割り当てようとしたら、少なくとも1組は被っちゃうよね。余裕で。鳩の巣原理ってこういうことなんだよ。
お〜、確かに。なんかすごい。
ようこちゃん、面白い例だね。確かに、直感的にはすごく当たり前に思える原理だけど、数学的にはかなり重要な原理だよ。大学入試でもこの原理を用いて証明する場面がたまに現れるから。
1989年第3問 高校数学を使えば簡単だが・・・
さぁ、いよいよ平面図形の問題。平面図形は解法がたくさんあるけど、中学数学で解いてみよう! ただ、中学生は「垂心」を知らないかもしれない。三角形で3つの頂点からでる垂線は1点で交わる、ということは既知として考えよう。じゃあ、ようこちゃん行く?
わたしか、、、。私は必要ならベクトルとか三角関数を使いたいよ。
そこをグッとこらえて、中学数学でやってみようよ。
そうだね、じゃあ、まずは絵を描くよ。
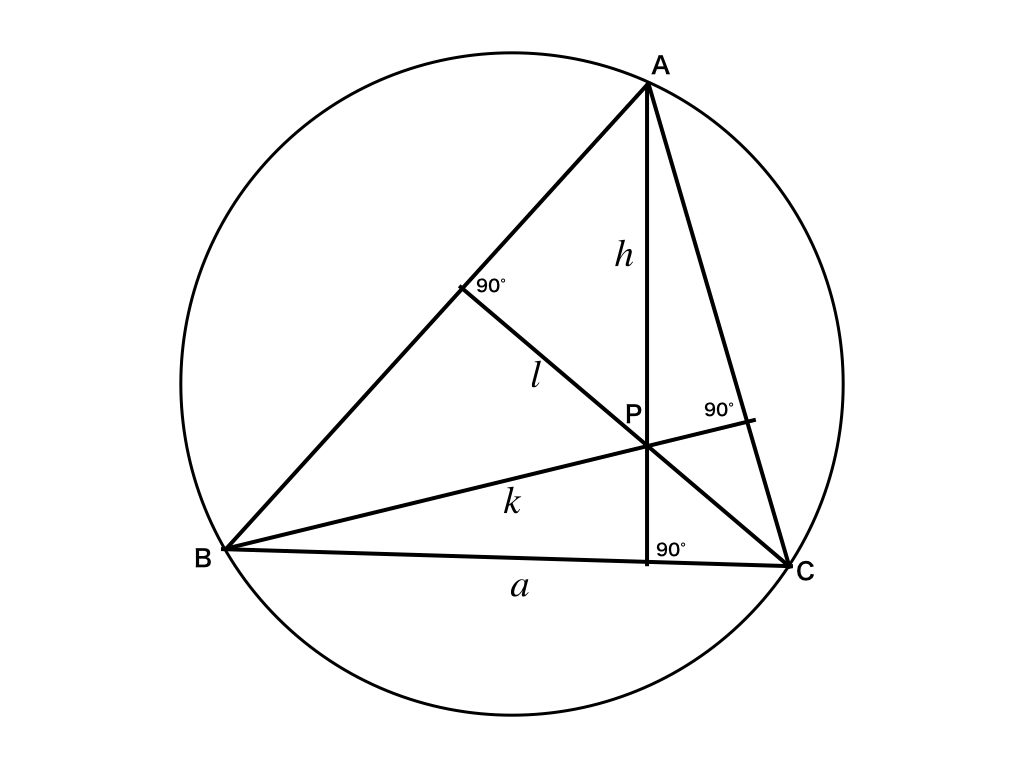
ん〜、角度を\(\theta\)とおいて、計算していきたいけどなぁ。それが使えないとなると、、。
ようこちゃん! あたしとの平面図形の特訓を思い出してよ。
わかってるよ、初等幾何で頑張れっていうんでしょ。初等幾何だと、使えるのは相似とかだよね。あとは三平方の定理とか、、、。試しに色々計算してみると。
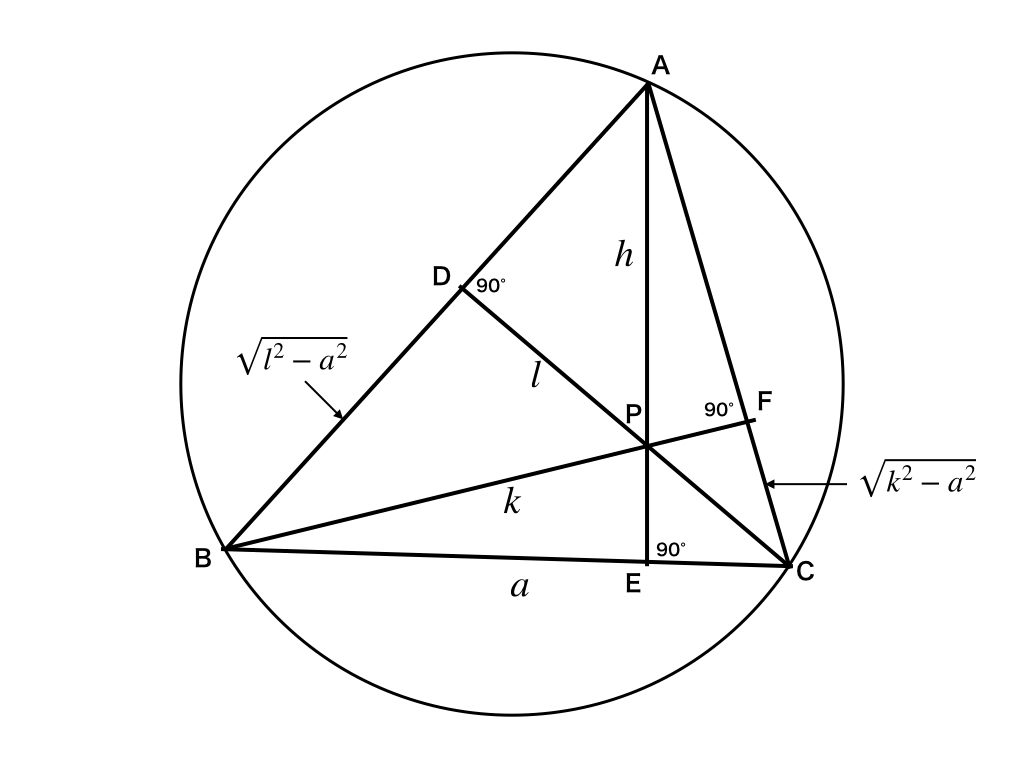
なんか、あんまり役に立たなそう。
ようこちゃんにヒント! こういう風に、ある値が一定であることを示せ、という問題では、今現在何が一定になっているかを考えてそれと結びつけるのがポイントだよ。
一定なのは、もちろん\(a\)の値だよね。他には、、、。あ、そうか。円周角の定理があるから、\(\angle BAC\)も一定だ。これらと\(h, l, k\)を結びつけたいんだけど。ん〜、なんとなく\(\triangle ADC\)が怪しいんだけど、例えば\(AC\)とか求まらないかなぁ。あれ、そうか、相似を使うと求められそう。
$$\triangle EAC \sim \triangle FBC$$
だから
$$EA : FB = BC : AC \leftrightarrow h : k = AC : a$$
となって
$$AC = \frac{ha}{k}$$
あ、これなら、
$$\sin{\angle BAC} = \frac{kl}{ha} \leftrightarrow a\sin{\angle BAC} = \frac{kl}{h}$$
となって、左辺は一定の値だから、右辺も一定になる!
ん〜! ようこちゃん、入試問題だったらそれでもいいんだけど、今日のルール!
あ、そうか、三角比はNGだったね。それなら、相似、使えばいいかな。\(\triangle CAD\)は点\(A\)が円上を動くとき、形は変わるけど、\(\angle CAD\)は一定、\(\angle CDA\)は\(90°\)ということは、どれも相似だ。相似な三角形の辺の比は等しいから、
$$\frac{ha}{k} : l = 一定 \leftrightarrow \frac{ha}{kl} = 一定 \leftrightarrow \frac{h}{kl} = 一定 \leftrightarrow \frac{kl}{h} = 一定$$
これでどうだ。
完璧! それなら中学数学の知識の範囲内だね! \(A\)が色々動くときの三角形を比べるとそれらが相似だからという理由で、辺の比が等しくなるんだね。高校生になると、「三角比」という単元でこれをもっと突き詰めていくから、この問題は最初にようこちゃんが思いついたように、パッと解けるんだよ。
うん、中学数学だけだと、ちょっと厄介だなぁ。
でも、頭の体操にはなるかも。なるべく初等的なものだけで解こうとすると、それだけ頭を使わないといけないからね。じゃあ、次の問題。
1969年第2問 数に踊らされるな、自ら踊れ
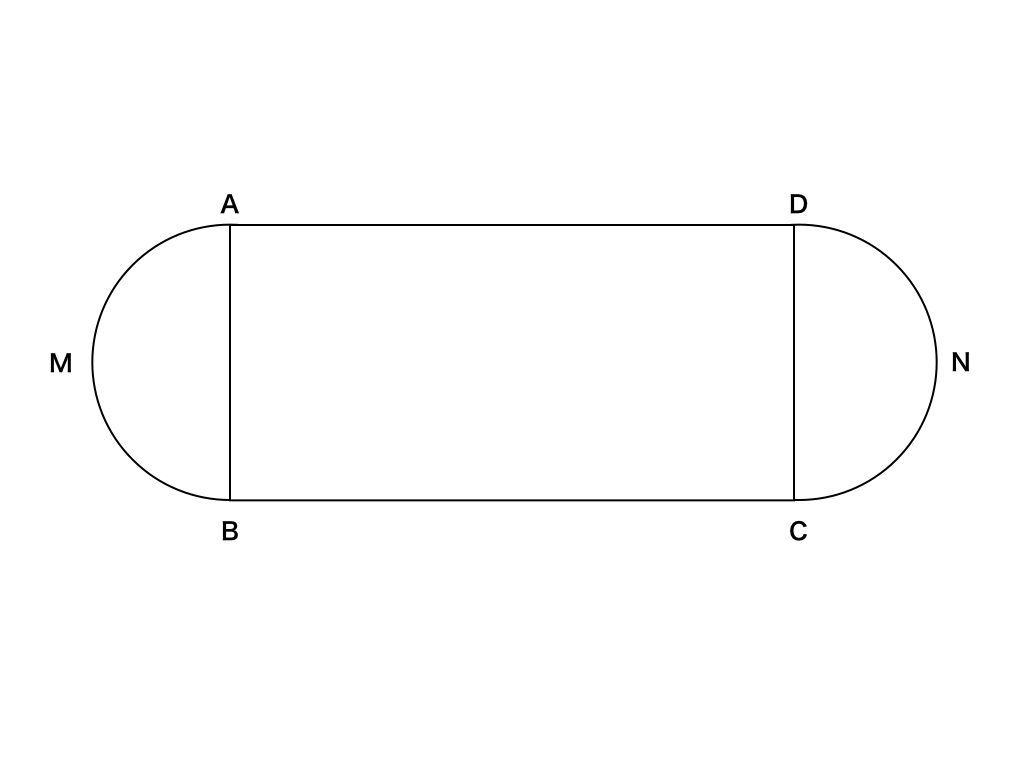
みよちゃん、どう?
私か、嫌な問題選んでくるね。
そう言わずに、頼むよぉ。
まぁ、いいよ。題材はシンプルだしね。じゃあ、方程式を2つ作るよ。それぞれ面積の式と周囲の長さ。
$$\pi r^{2}+2xr = 7000$$
$$2\pi r + 2x = 400$$
これで、上の式をちょっと工夫して
$$2\pi r^{2} + 2xr -\pi r^{2} = 7000 \leftrightarrow (2\pi r+2x)r – \pi r^{2} = 7000$$
とすると下の式をそのまま代入できるから
$$\pi r^{2} – 400 r + 7000 = 0$$
$$11r^{2} – 1400r + 24500 = 0$$
みよちゃん、賢い! それならただの2次方程式だから中学生でもやれるね。
めんどくさいけど。じゃあ解の公式で解くと
$$\begin{eqnarray}
r &=& \frac{700\pm \sqrt{700^{2}-11\times24500}}{11}\\
&=& \frac{700\pm 10\times\sqrt{4900-11\times245}}{11}\\
&=& \frac{700\pm 10\times\sqrt{2205}}{11}\\
&=& \frac{700\pm 10\times21\sqrt{5}}{11}\\
&=& \frac{700\pm 210\sqrt{5}}{11}
\end{eqnarray}$$
で、求めたいのは\(2r\)だから
$$AB = 2r = \frac{1400\pm 420\sqrt{5}}{11}$$
だけど、注意しなければならないのは符号。この場合適切なのはマイナスだけだから答えは
$$AB = 2r = \frac{1400- 420\sqrt{5}}{11}$$
みよちゃん、最後の大事な確認も見事に突破してるね、さすが!
あれ、プラスはダメなの?
みうちゃん、プラスを選んだ時の\(2\pi r\)ってどのくらい?
$$2\pi r = \pi \times \frac{1400 + 420\sqrt{5}}{11}$$
ああ、私は、今日こんな役回りばっかだよ!
分子は2000くらいだから、だいたい600くらいかな。
うん! 重要なのは400を超えるかどうかっていうところだよ。
$$2\pi r + 2x = 400$$
この式があって\(x\)は当然正だから、そうなるものを選ばないとダメだよね。それで概算すると、
$$2\pi r \geq \pi \times \frac{2200}{11} \geq 600 $$
になっちゃうから、\(x\)が負になっちゃうので不適ってことだね。解答欄に書くときは、これもつけておかないと。
平易な問題のときは、こういう細かい確認が合否を分けるから、気をつけないとダメだね。今回は割とわかりやすい確認だけど。
そうそう。レベルの高い入試問題ほど、こういう嫌なところを突いてくるから、習慣づけておかないとね。
1999年第1問 中線定理?
$$AB^{2} + AC^{2} \geq 2AP^{2} + BP^{2} + CP^{2}$$
となることを示せ
じゃあ、これはあたしがやろっかな。
中線定理という公式があって、それを使うと
$$AB^{2}+AC^{2} = 2(AM^{2} + BM^{2})$$
という公式が成り立っている。今回は使わないけど、題材は似ているかも。この問題は基本的に三平方の定理でできそうだね。
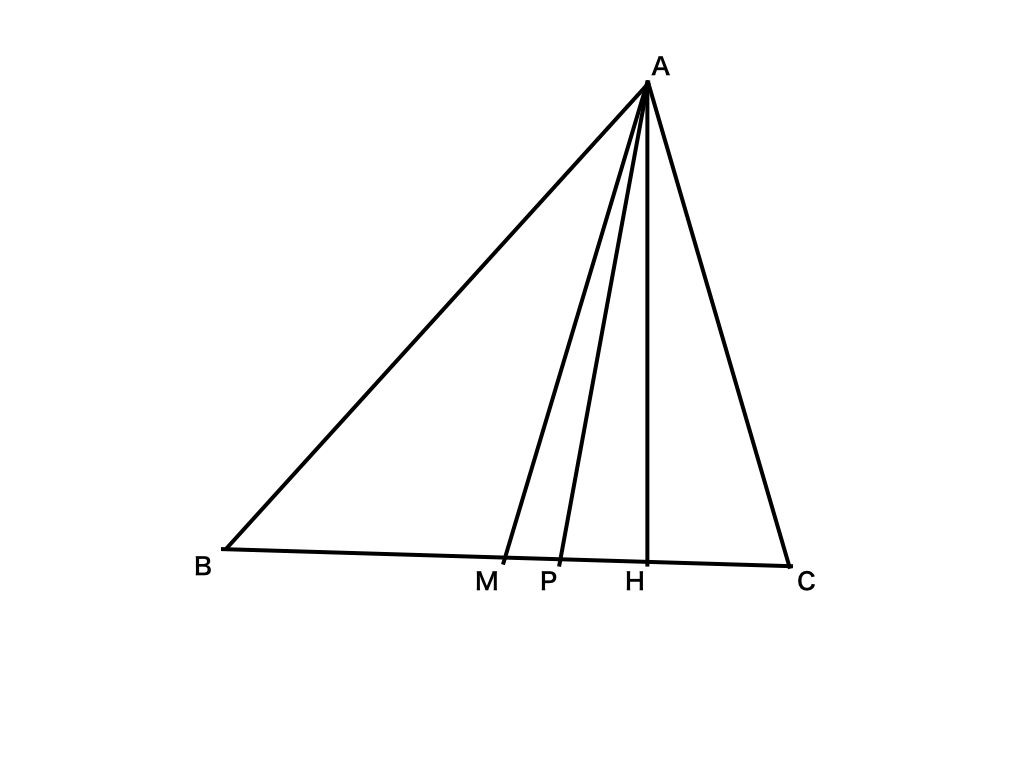
[1] 点\(H\)が中点\(M\)に対して\(A\)側にあるとき、つまり\(AB>AC\)のとき、
$$AH^{2} + CH^{2} = AC^{2}$$
$$BH^{2} + AH^{2} = AB^{2}$$
へんぺん足すと
$$\begin{eqnarray}
AB^{2} + AC^{2} &=& 2AH^{2} + BH^{2} + HC^{2}\\
&=& 2AP^{2} – 2PH^{2} + BH^{2} + HC^{2}\\
\end{eqnarray}$$
ここで、\(AH^{2} = AP^{2}-PH^{2}\)という式を使ったよ。問題文の式から、証明したいのは\(AP\)に関するものだからね。こういう感じで、成り立つ式から証明したい式に使われているものへと変形していくことが1つの方針かな。
最後は\(BP, CP\)を使いたいよね。だから、\(CH = CP-PH, BH = BP+PH\)が使えそうだから最終的に
$$AB^{2} + AC^{2} = 2AP^{2} + CP^{2} + BP^{2} + 2PH(BP-CP)$$
が出てくる。冒頭で話したように不等式の証明は求めたい式の左辺から右辺を引けばいいんだから、
$$AB^{2} + AC^{2} – (2AP^{2} + CP^{2} + BP^{2})$$
が0以上となることを示せばいい。今、
$$AB^{2} + AC^{2} – (2AP^{2} + CP^{2} + BP^{2}) = 2PH(BP-CP)$$
だけど、点Pは線分\(MH\)上に取るから\(BP \geq CP\)だから
$$AB^{2} + AC^{2} – (2AP^{2} + CP^{2} + BP^{2}) = 2PH(BP-CP) \geq 0$$
よって、この場合は問題文の条件が成り立つ。
[2] 点\(H\)が中点\(M\)に対して\(B\)側にある時、つまり\(AB<AC\)のときも同様に計算できる。
さて、これで終わりかな?
あれ? \(AB=AC\)のときはいいの?
みうちゃん、ナイス。そうだね。その時も確認が必要だね。
[3] \(AB=AC\)のとき、
この場合、\(M, H, P\)は一致するので、
$$\begin{eqnarray}
AB^{2} + AC^{2} &=& 2AH^{2} + BH^{2} + HC^{2}\\
&=& 2AP^{2} + BP^{2} + CP^{2}
\end{eqnarray}$$
となって、問題文の条件を満たすね。だから、いずれの場合も不等式が満たされる。
ちなみに、不等式の等号が成立するのは、\(P\)が点\(M\)に一致するときで、それは結局
$$AB^{2} + AC^{2} = 2AP^{2} + BP^{2} + CP^{2} = 2AP^{2} + 2BP^{2}$$
だから、中線定理のことを指しているよね。
ようこちゃんもいいポイントだね。うん、この問題は中線定理を含んだより拡張された式のことだったんだね。次は、またサイコロを使った問題だよ。いびつな形をしたサイコロの不思議な性質だね。
1979年第4問 いびつなサイコロに隠れた不思議な性質
(ⅰ) 引き分けになる確率\(P\)を求めよ。
(ⅱ) \(P\geq \frac{1}{6}\) であることを示せ。また\(P=\frac{1}{6}\)ならば\(p_{k} = \frac{1}{6}\)である\(k=1, 2, 3, 4, 5, 6\)ことを示せ。
これ、面白そうかも。やってみてもいい?
はい、じゃ、えりちゃん、お願いします。
え〜と、1問目は簡単だよね。引き分けになるってことは2人とも同じ目をだすということなんだから
$$P = p_{1}^{2} + p_{2}^{2} + p_{3}^{2} + p_{4}^{2} + p_{5}^{2} + p_{6}^{2}$$
問題は2問目。とりあえず、確率の和が1だから
$$p_{1} + p_{2} + p_{3} + p_{4} + p_{5} + p_{6} = 1$$
が成り立ってる。
高校数学の範囲で習う、コーシー・シュワルツの定理の6次元拡張バージョンを使えば一瞬で求められるんだけど、まぁそれは使わない約束だからね。
1文字を代入していくというのもちょっと嫌だなぁ。考え方としては、\(p_{1}\)とか\(p_{2}\)とかっていうのは、\(\frac{1}{6}\)からずれた値になってるってことなんだよね。このずれがどのくらいかっていうことがわからないんだけど。
えりちゃん、それ、いいよ。そのずれを定量的に表すとどうなる?
ん? ずれを定量的に表す? っていうのはある実数を例えば\(\delta_{1}\)として
$$p_{1} = \frac{1}{6} + \delta_{1}$$
のように表すってこと?
そうそう! その変形って6つの\(\delta\)を使えば、全ての\(p_{k}\)を置き換えられるよね。それを今までの2つの式に代入するとどうなる?
え〜と、まず和が1になる式からは
$$\delta_{1} + \delta_{2} + \delta_{3} + \delta_{4} + \delta_{5} + \delta_{6} = 0$$
という式が出てくる。それで、\(P\)に関する式は
$$\begin{eqnarray}
P &=& (p_{1}+\delta_{1})^{2} + (p_{2}+\delta_{2})^{2} + (p_{3}+\delta_{3})^{2} + (p_{4}+\delta_{4})^{2} +(p_{5}+\delta_{5})^{2} + (p_{6}+\delta_{6})^{2} \\
&=& \frac{1}{6} + \delta_{1}^{2} + \delta_{2}^{2} + \delta_{3}^{2} + \delta_{4}^{2} + \delta_{5}^{2} + \delta_{6}^{2} + 2(\delta_{1} + \delta_{2} + \delta_{3} + \delta_{4} + \delta_{5} + \delta_{6})\\
&=& \frac{1}{6} + \delta_{1}^{2} + \delta_{2}^{2} + \delta_{3}^{2} + \delta_{4}^{2} + \delta_{5}^{2} + \delta_{6}^{2}
\end{eqnarray}$$
あれ? そうか! 実数の2乗は0以上だからこの右辺は、
$$\frac{1}{6} + \delta_{1}^{2} + \delta_{2}^{2} + \delta_{3}^{2} + \delta_{4}^{2} + \delta_{5}^{2} + \delta_{6}^{2} \geq 0$$
になっているんだ!
そうなんだよ! こんな感じでパラメータを「ずれ」を表すものに切り替えると式が劇的にみやすくなるということがあるんだ。統計学でいう「偏差」という考え方と似ているね。この形なら後半の方も簡単に証明できるね。
そうだね。まみちゃんが最初に説明してくれたように、
$$\delta_{1}^{2} + \delta_{2}^{2} + \delta_{3}^{2} + \delta_{4}^{2} + \delta_{5}^{2} + \delta_{6}^{2} = 0$$
となる実数は全てが0になっていなければいけないから、結局ずれはなしで
$$p_{k} = \frac{1}{6}\ (k=1, 2, 3, 4, 5, 6)$$
になるということだね。
うん、綺麗にまとまったね。
なるほど、パラメータを中心からの差におきかえるとうまくいくことがあるんだね! 勉強になった。
ところで、さっきまみちゃんが言ってた、コーシー・シュワルツの不等式って
$$(ax+by)^{2}\leq (a^{2}+b^{2})(x^{2}+y^{2})$$
という式だよね。これを使えるの?
実際には、6次元の
$$(a_{1}x_{1}+a_{2}x_{2}+\cdots+a_{6}x_{6})^{2}\leq (a^{2}+a_{2}^{2}+\cdots+a_{6}^{2})(x_{1}^{2}+x_{2}^{2}+\cdots+x_{6}^{2})$$
という式を使うよ。これは出てくる文字が全て実数の時に成り立つ式だからどんな実数を代入してもいい。つまり
$$a_{1} = a_{2} = a_{3} = a_{4} = a_{5} = a_{6} = 1$$
$$x_{1} = p_{1}, x_{2} = p_{2}, x_{3} = p_{3}, x_{4} = p_{4}, x_{5} = p_{5}, x_{6} = p_{6}$$
を代入すると、
$$(p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6})^{2}\leq 6\times P$$
という式になるから
$$\frac{1}{6}\leq P$$
が出てくるね。ちなみに、等号成立条件は
$$a_{1} : a_{2} : a_{3} : a_{4} : a_{5} : a_{6} = p_{1} : p_{2} : p_{3} : p_{4} : p_{5} : p_{6}$$
だから、
$$1: 1: 1: 1: 1: 1 = p_{1} : p_{2} : p_{3} : p_{4} : p_{5} : p_{6}$$
となって、どの確率も同じ時、つまり\(p_{k} = \frac{1}{6}, k=1, 2, 3, 4, 5, 6\)となることがわかるんだ。
わぁ、鮮やかだね。でも、6次元のコーシー・シュワルツの方程式なんて、どうやって証明するの? まさか、展開するわけじゃないよね?
展開しても証明できるよ! ただ、普通はもっと賢く証明する。じゃないと\(n\)次元になった時に通用しないからね。コーシー・シュワルツの不等式の証明は感動するほどエレガントの証明がいくつもあるから、色々調べてみると面白いかも。あたしは、判別式を使うのが一番好きかな。
さて、いよいよラストスパート。あと2問だよ。
1989年第2問 不等式の仕掛け
このような\(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\)を全て求めよ。
(*作者注)
\(a_{1}, a_{2}\)の相加平均とは、\(\frac{a_{1}+a_{2}}{2}\)のことである。
じゃあ、これは眠そうなみよちゃんに解いてもらおうかな。
あ、バレてた。次はどの問題?
次はこれ。さっきとは全然タイプの違う問題だよ。
う〜ん。なるほど。……わかった、かな。
はや! じゃあ、どうぞ。
まず、\(a_{1} ~ a_{5}\)について順序を決めて
\(a_{1}\leq a_{2} \leq a_{3}\leq a_{4} \leq a_{5}\)
としても良い。このとき
[1]
$$a_{5} \leq \frac{a_{1}+a_{2}+a_{3}+a_{4}}{4} \leq \frac{a_{4}+a_{4}+a_{4}+a_{4}}{4} = a_{4}$$
が成り立つ。ただし、最初に決めた順序と組み合わせると
$$a_{4}\leq a_{5} \leq a_{4}$$
だから、これを満たすためには\(a_{4} = a_{5}\)でなければならない。
[2]
$$a_{4} \leq \frac{a_{1}+a_{2}+a_{3}+a_{5}}{4} = \frac{a_{1}+a_{2}+a_{3}+a_{4}}{4}$$
について考える。
$$\frac{3a_{4}}{4} \leq \frac{a_{1}+a_{2}+a_{3}}{4} \leq \frac{3a_{3}}{4}$$
よって\(a_{4}\leq a_{3}\)だから最初に決めた順序と組み合わせると
$$a_{3}\leq a_{4} \leq a_{3}$$
よって、\(a_{4} = a_{3}\).
[3]
$$a_{3} \leq \frac{a_{1}+a_{2}+a_{4}+a_{5}}{4} = \frac{a_{1}+a_{2}+a_{3}+a_{3}}{4}$$
について考える。
$$\frac{a_{3}}{2} \leq \frac{a_{1}+a_{2}}{4} \leq \frac{a_{2}}{2}$$
よって\(a_{3}\leq a_{2}\)だから最初に決めた順序と組み合わせると
$$a_{2}\leq a_{3} \leq a_{2}$$
よって、\(a_{3} = a_{2}\).
[4]
$$a_{2} \leq \frac{a_{1}+a_{3}+a_{4}+a_{5}}{4} = \frac{a_{1}+a_{2}+a_{2}+a_{2}}{4}$$
よって\(a_{2}\leq a_{1}\)だから最初に決めた順序と組み合わせると
$$a_{1}\leq a_{2} \leq a_{1}$$
よって、\(a_{2} = a_{1}\).
以上より、\(a_{1} = a_{2} = a_{3} = a_{4} = a_{5} = a\)となることが必要であり、これは実際に問題文の条件を満たす。
よってある実数を\(a\)として求めるものは
$$(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}) = (a, a, a, a, a)$$
となる。
うん、綺麗だね。ちなみに、理系の問題は5つじゃなくて\(n\)個にしているけど、証明の作戦自体はほとんど同じで、文字を使って示さないといけなくなっているよ。
こういう問題って、最初に順序を決めて解くことが多いけど、それって問題ないのかな。
それは、この問題に関していえば、問題ないと思うよ。例えば、条件を満たすある5つの実数が決まったとして、それを小さい順に並べたあと改めて\(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\)と定義したとするよね。それで、順番はともかく、数字の組は1つ決まることになる。で、今は全てが等しい場合しかないから、それを並び替える必要がない。
ってことは、問題文の条件を満たす組み合わせの中に、全てが同じじゃないものがあれば、順番を変えたものも答えにしないといけないということ?
そうだね。この方法では、5つの数字の組のなかで、順番を一つに固定したものだけを求めることができるからね。もし、同じ数字じゃないんだったら、順番を変えたものも答えになる。ただ、どちらにしても、あたしの方法で求められるよ。
うん、こういう風にいくつかの実数とか整数があってそれの組みを全て求めよ、という問題ではみよちゃんがやったように、大きさの順番を自分で仮定してしまうというのが解きやすくするポイントかな。
じゃあ、最後は幾何で締めくくろう!
1988年第2問 マトリョーシカ?
この問題、たぶん、ようこちゃんだったらベクトルで解きたくなるような問題だよね。実際、ベクトルを使うと、あっという間に示すことができるんだけど、今回は中学数学縛りだから、ベクトルはなしね。最後の問題だし、みんなで解いちゃおっか。
とりあえず、図を書いてみるね。
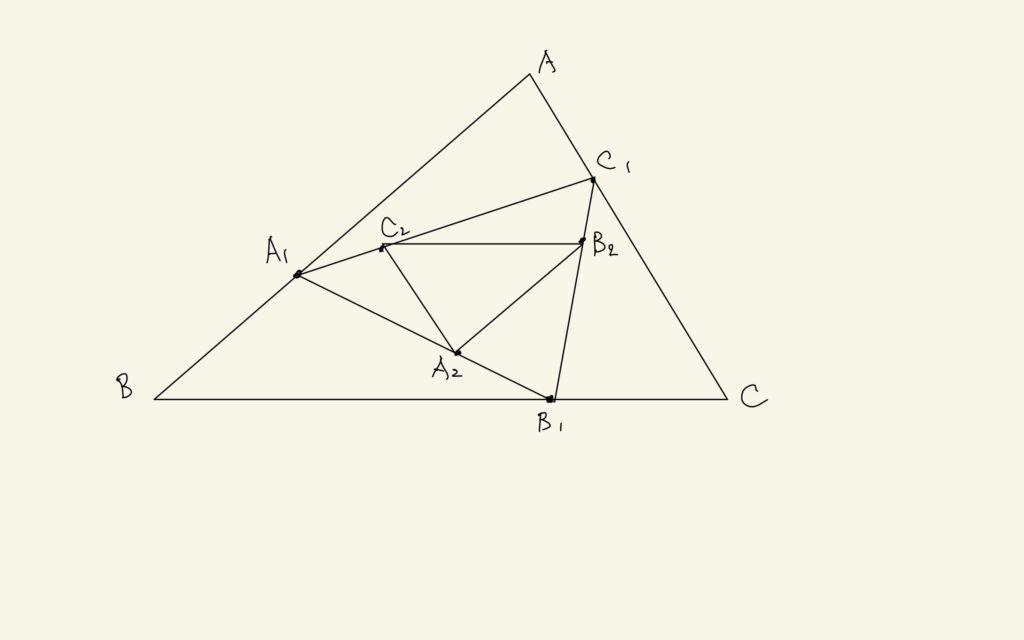
ベクトルじゃないんだったら初等幾何的に解く?
じゃあ、補助線がいるよね。
みうちゃん、補助線引いてみてよ!
え? あたしでいいの? じゃあ、適当に高校入試の感覚で引いちゃうよ。
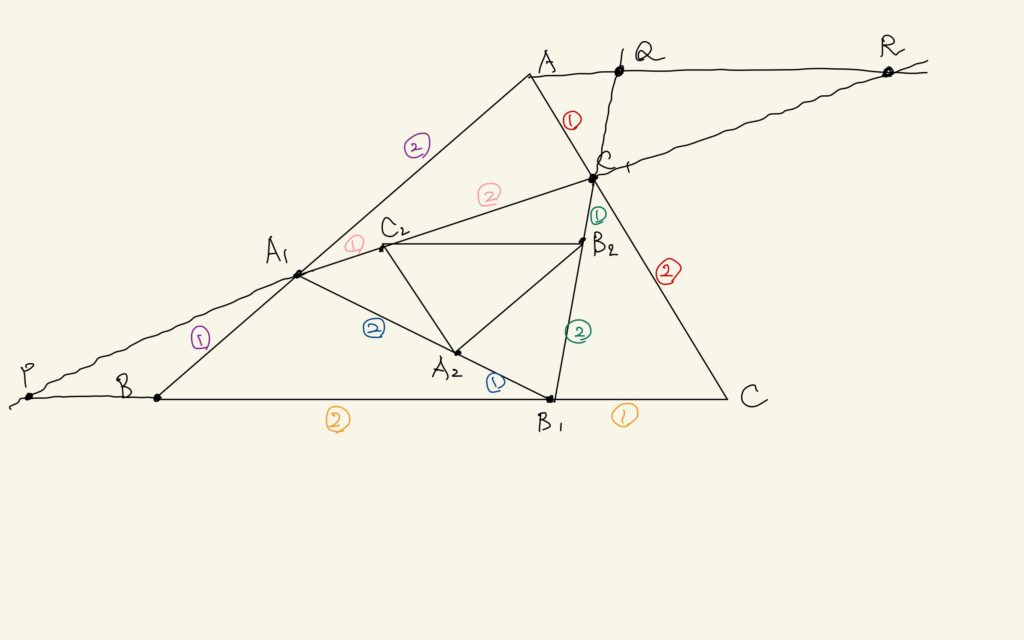
うわ〜、いっぱい引いたね。
うん! 高校入試の時には、とにかく「砂時計」を作るイメージで補助線を引いてたから。
あ、その感覚わかる! 平行四辺形とかが出てきた時、わたしもよくそうしてた。
じゃあ、ここから何がわかるかな?
方針としては、いろんな所の辺の比を求めていくことだね。
じゃあ、私から、こういうのを付け足すことはできるよね?
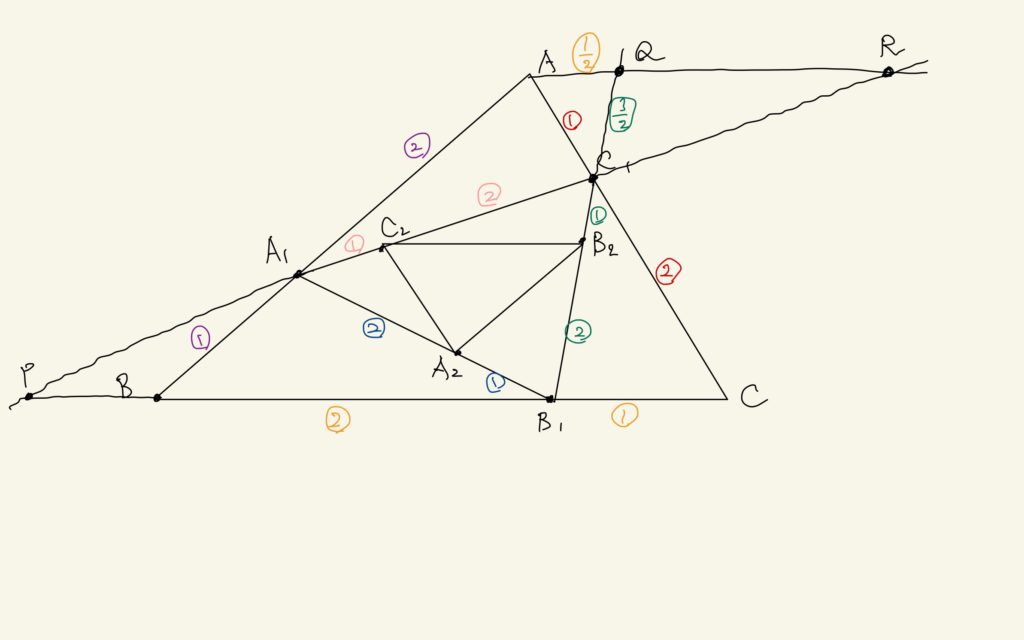
そうだね! 緑の\(\frac{3}{2}\)と黄色の\(\frac{1}{2}\)を追加したんだね。うん、それは
$$\triangle AQC_{1} \sim \triangle CB_{1}C_{1}$$
を使えばわかるね。
う〜ん、次のステップが難しいなぁ。
確かに、簡単には出せそうにないかなぁ。
みよちゃんはどう? 何か見える?
見えるっていうか、例えば\(QR=x, PB=y\)とおいたら、先に進むんじゃない?
あ、そうか。辺の比を文字でおいちゃうってことだね。同じ色の辺の比なら比較できるから、そういう置き方はありだ。
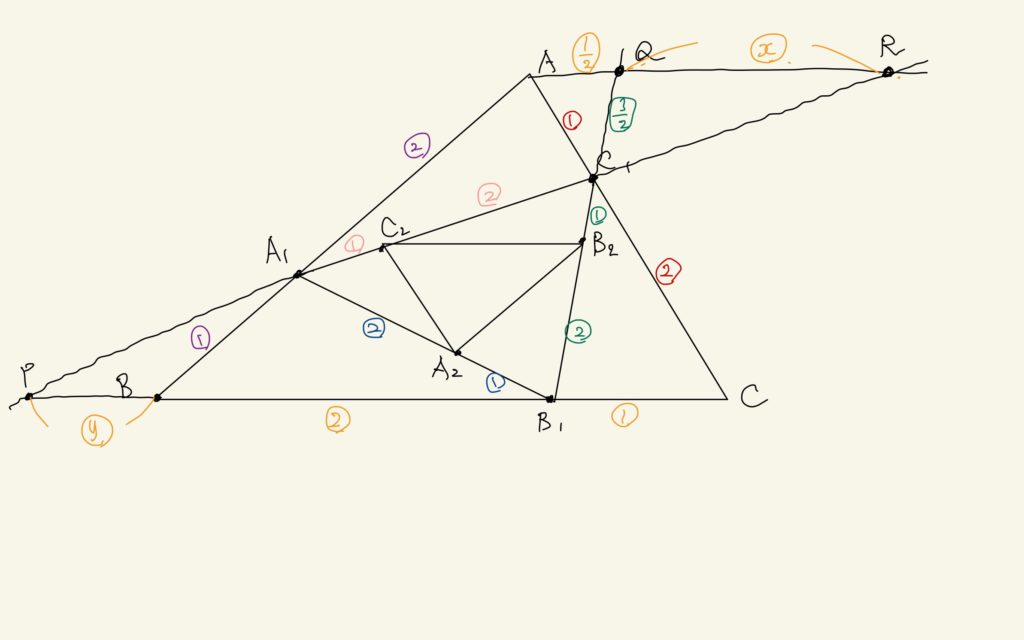
確かに、そうすると式がたちそうだね。
え〜と、そうか! 一つ目は\(\triangle QRC_{1} \sim \triangle B_{1}PC_{1}\)を使って
$$x : y+2 = 3:\frac{3}{2} = 1 : 2 \leftrightarrow 2x = y+2$$
だね。
もう一つ目は、\(\triangle ARC_{1} \sim \triangle CPC_{1}\)を使って
$$x+\frac{1}{2} : y+3 = 1 : 2 \leftrightarrow 2x+1 = y+3$$
かな。あれ? 違うか。これだとえりが出したのと同じ式になっちゃう。じゃなくて、\(\triangle ARA_{1} \sim \triangle BPA_{1}\)か。これで
$$\frac{1}{2}+x : y = 2 : 1 \leftrightarrow \frac{1}{2}+x = 2y$$
だ。これとえりの出した式を連立すると?
はい! それは私がやります。連立すると
$$y = 1, x = \frac{3}{2}$$
が出てきました。書き込んどくね。
同じように、こういうことをしてみる?
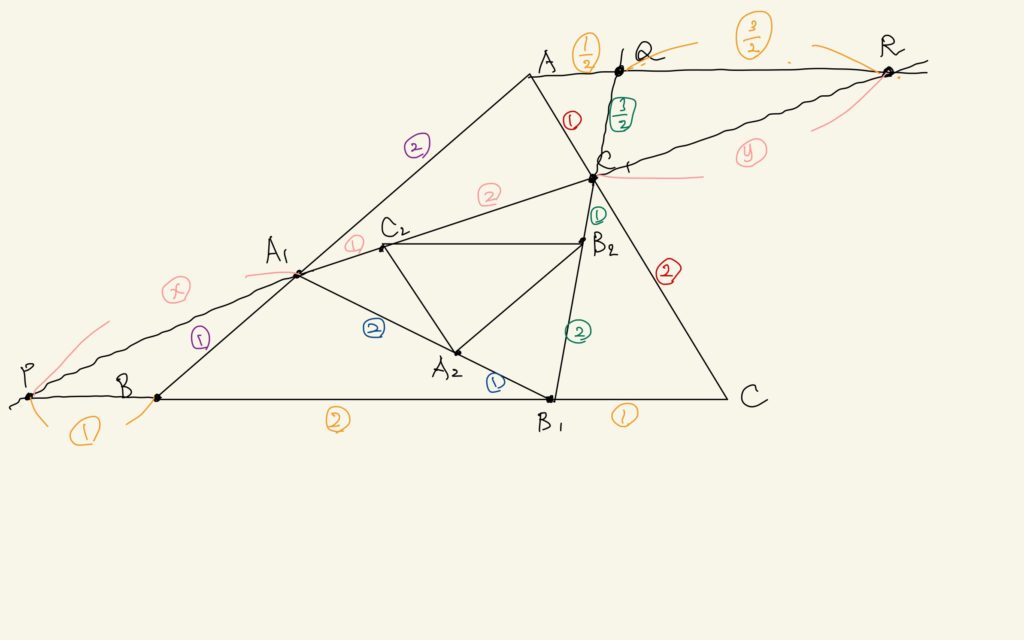
じゃあ、今度は私が式を立てるね。まず\(\triangle ARA_{1} \sim \triangle BPA_{1}\)を使って
$$x : y+3 = 1 : 2 \leftrightarrow 2x = y+3$$
もう一つは、(\triangle QRC_{1} \sim \triangle B_{1}PC_{1}\)を使って
$$3 : \frac{3}{2} = 2 : 1 = x+3 : y \leftrightarrow 2y = x+3 $$
連立すると
$$x = 3, y = 3$$
みうちゃん、ナイス。ってことは最終的にこうなる!
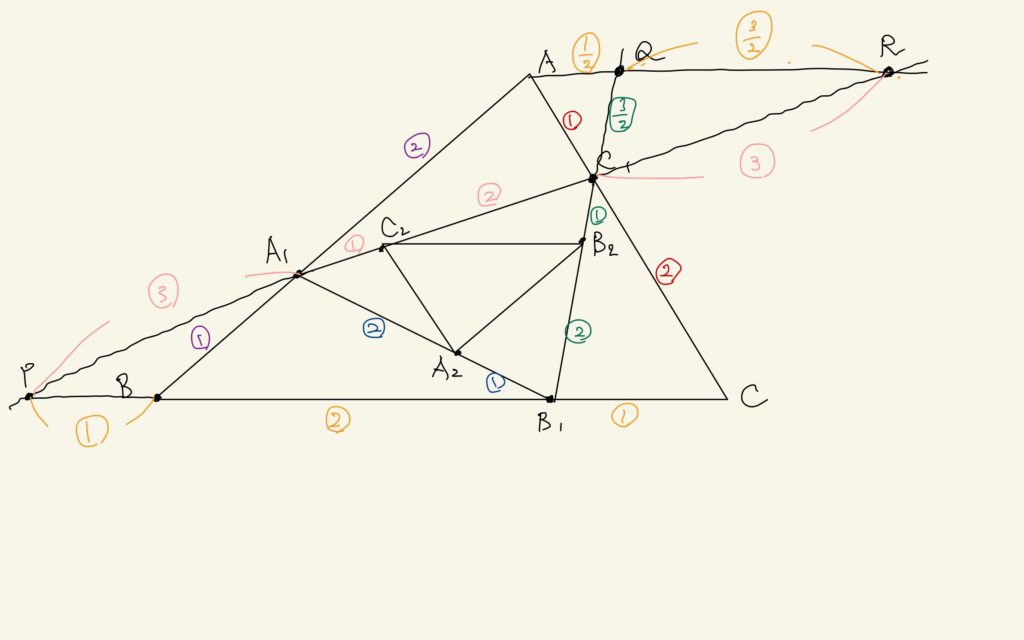
さぁ、これで何か気づくかな?
あ、わかった!
$$\triangle QRC_{1} \sim \triangle B_{2}C_{2}C_{1}$$
だね。
うん! 正解。
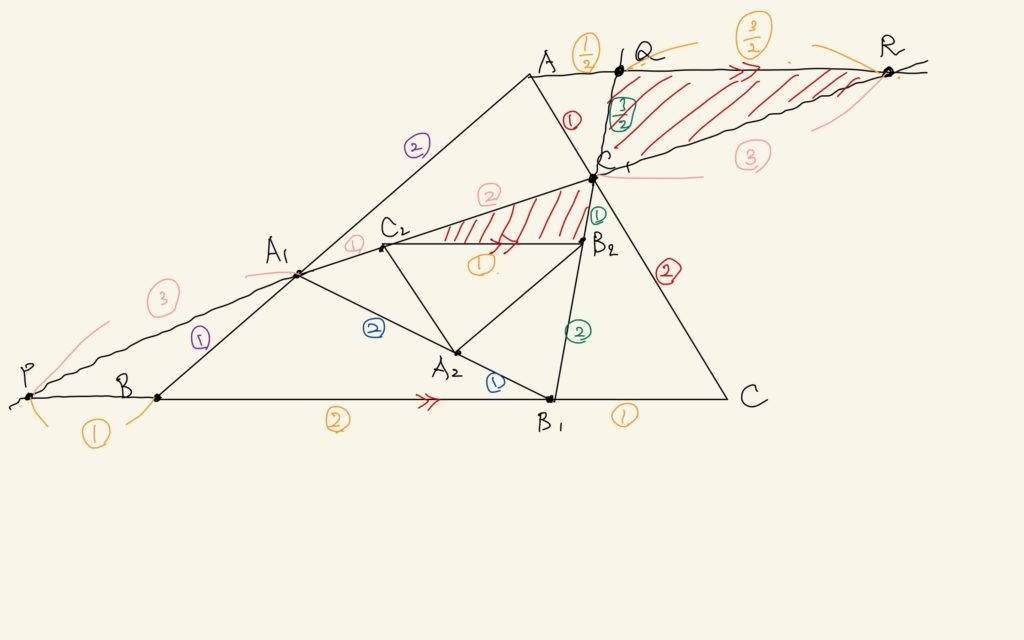
なるほど、そうすると、\(QR//C_{2}B_{2}//BC\)だね。それで
$$BC : C_{2}B_{2} = 3 : 1$$
なんだね。あとはこれを右側に回転させて、頂点\(B\)が上にくるようにすると、辺の比の関係性が、今の場合と全く同じだから、同じように計算することで
$$A_{2}B_{2}//AC$$
を示せる。また、さらにそれを右側に回転させて頂点\(C\)が上にくるようにすると、辺の比の関係性がやっぱり全く同じだから、
$$A_{2}B_{2}//AB$$
であることを示せる。
それなら、こんな感じで2組の角が等しいことを示せるんだね。
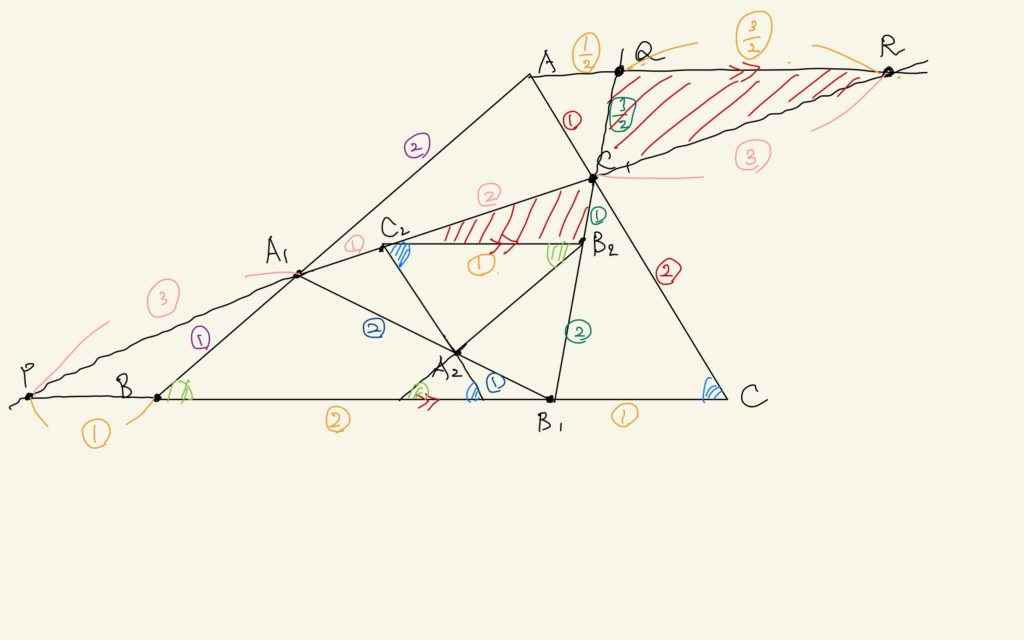
ということで、
$$\triangle ABC \sim \triangle A_{2}B_{2}C_{2}$$
になるわけだ。
みうちゃん、おいしいところを持っていったね。うん、そういう感じで示すことができるね。ただ、みうちゃんの補助線だとかなりややこしいかも。たぶん、もっといい補助線があったと思うけど、まぁ、それはいいことにしよう!
ところで、これを高校数学だとどう解けるのか、それはようこちゃんに任せようかな。
あ、ベクトル使っていいんだ。それなら任せてよ!
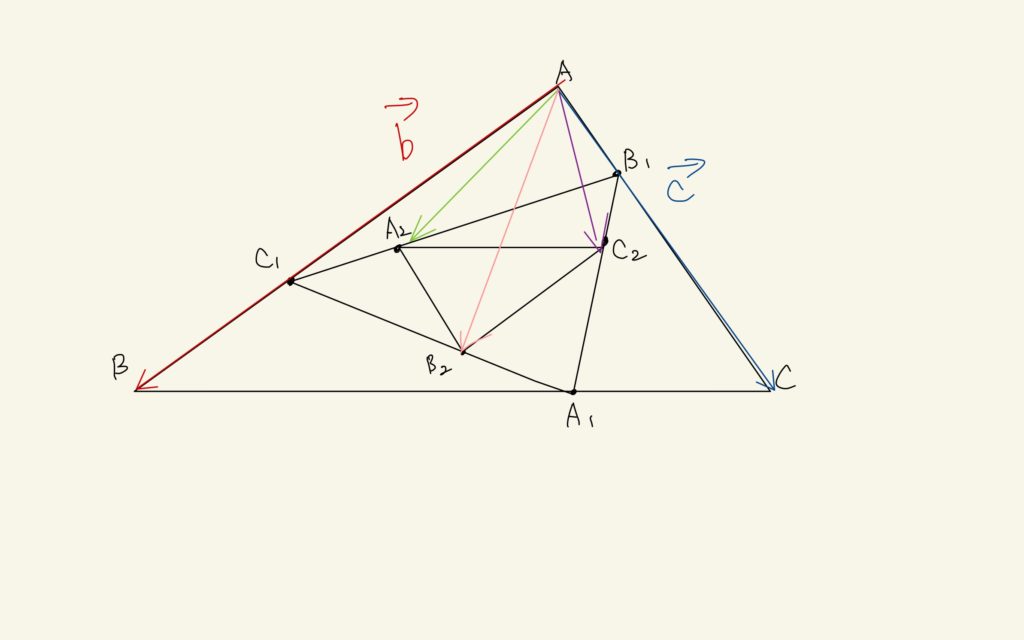
こんな風にベクトルを設定するね。そうすると、
$$\overrightarrow{AA_{2}} = \frac{2}{3}\frac{2}{3}\vec{b} + \frac{1}{3}\frac{1}{3}\vec{c}$$
$$\overrightarrow{AB_{2}} = \frac{1}{3}\frac{2}{3}\vec{b} + \frac{2}{3}\left( \frac{1}{3}\vec{b} + \frac{2}{3}\vec{c}\right)$$
$$\overrightarrow{AC_{2}} = \frac{1}{3}\left( \frac{1}{3}\vec{b} + \frac{2}{3}\vec{c} \right) + \frac{2}{3}\frac{1}{3}\vec{c}$$
だから、それぞれ
$$\overrightarrow{AA_{2}} = \frac{4}{9}\vec{b} + \frac{1}{9}\vec{c}, \overrightarrow{AB_{2}} = \frac{4}{9}\vec{b} + \frac{4}{9}\vec{c}, \overrightarrow{AC_{2}} = \frac{1}{9}\vec{b} + \frac{4}{9}\vec{c}$$
なので、
$$\overrightarrow{A_{2}C_{2}} = \frac{1}{3}(\vec{b}-\vec{c}) = \frac{1}{3}\overrightarrow{BC}$$
$$\overrightarrow{C_{2}B_{2}} = \frac{1}{3}\vec{b} = \frac{1}{3}\overrightarrow{AB}$$
$$\overrightarrow{A_{2}B_{2}} = \frac{1}{3}\vec{c} = \frac{1}{3}\overrightarrow{AC}$$
となるから
$$A_{2}C_{2}//BC, C_{2}B_{2}//AB, A_{2}B_{2}//AC$$
となって同じ平行条件が導かれるね。
さすが、ようこちゃん、完璧なベクトル捌きだね。そうなんだ。ベクトルを使うとややこしい比の計算や補助線なしで、一発で答えを導ける。幾何の問題に対してベクトルは凄まじい破壊力を持つんだよ。
今日はこんな感じかな。みんな、どうもありがとう! おかげで楽しかったよ。
私も! ありがとう。
今日が初めてだったけど、またやろうね!
ぜひお願いします。
みよちゃんもね!
わかってるよ。



コメント