さぁて、今日はいよいよ物理をやる時間だね。まみ、準備はいい?
準備万端!
ようこちゃん、まみちゃん、今日はわたしも参加していい?
もちろん。是非参加してよ。
お、えりちゃん、久しぶり。えりちゃんは化学派だよね。物理も興味あるんだ。
うん。今日はさ、ちょっと時間があってね。ちなみに、どうやって進めるの?
そうだねぇ。私たちも初めてなんだけど、京都大学の物理は問題文が長いから、少しずつ取り出す感じでやればいいかな。
今回のテーマは相対論! と言っても、問題は非常にシンプルな波動と力学の問題だから安心してね。
相対論って、アインシュタインが考えた相対論? 大学の物理だよね?
うん、基本はね。でも問題の中ではその結果を使っているだけだから、大丈夫。じゃあ、まずは京都大学からの説明、ね。

おっ、近似を使うんだね。
うん。基本的に、高校物理では2次以上の微小量を無視することになっているから、この近似は普通なんだよ。でも、数学的になぜこれで近似できるか、まみなら説明できる?
そうだねぇ、確か教科書にも近似は載っていたと思う。数学的には、微小量の近似はテーラー展開で求められる。
\(f(x) = \frac{1}{1-x}\)とおくと\(f(x)\)は何階でも微分可能だから、\(x=a\)周りでのテーラー展開は
$$f(x) = f(0) + f^{\prime}(a)x + \frac{f^{\prime\prime}(a)}{2!}x^{2} + \frac{f^{\prime\prime\prime}(a)}{3!}x^{3} + \cdots + \frac{f^{(n)}(a)}{n!}x^{n} + \cdots$$
と続いて、これを2次式までで近似すると
$$f(x) \simeq f(0) + f^{\prime}(a)x + \frac{f^{\prime\prime}(a)}{2!}x^{2}$$
それで、今は微小量の近似をしたいので、\(a=0\)とおいて
\(f(x) \simeq f(0) + f^{\prime}(0)x + \frac{f^{\prime\prime}(0)}{2!}x^{2}\)
となる。あとは\(f(x)\)を微分していけばいいんだ。2次の微小量を無視するなら
\(f(x) \simeq f(0) + f^{\prime}(0)x\)
だから、1回微分だけ考えて
$$f^{\prime}(x) = (1-x)^{-2}$$
ここに\(x=0\)を代入すると\(f^{\prime}(0) = 1\)。よって\(x\)が微小量なら
$$f(x) \simeq 1 + x$$
\(x = \epsilon\)と置き換えると、問題文のものと一致するね。ちなみに、もう一つの近似式は、展開して出てくる式のうち、2次以上の微小量を無視した式になってるよ。
うん、さすがまみだね。そういう近似を使っている。この問題では、この近似をバンバン使うから、重要だよ。
問題 (1) – 1 光のドップラー効果

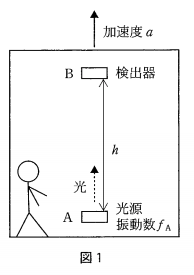
これは問題のほんの一部だけど、さぁ、解いてみよう。
え〜と、つまりエレベータに人がいるみたいな状況かな? その中に光源があって、エレベータの別の場所にある検出器に光を送ることを考えているんだ。ところで、ドップラー効果って、すぐ忘れちゃうんだけど、、、。
う〜んと、公式はおぼえてるよ。
普通は音源を使う。音の速度を\(c\), その音源が観測者に向かってうごく速度を\(v_{A}\), 観測者がうごく速度を\(v_{B}\)とすると、静止した音源の振動数\(f_{A}\)と観測者がきく音源の振動数\(f_{B}\)の関係は
$$f_{B} = \frac{c-v_{B}}{c-v_{A}}f_{A}$$
だったよね?
そうそう。えりの場合だと、音源から観測者に向かう向きを「正」とおいているんだね。今は音じゃなくて光を考えているけど、公式は同じだね。本当に厳密には、速度が光速に近い場合は特殊相対論的な考え方が必要だけど、今はそういう状況じゃないからこの公式が使えるよ、ってことだね。
あっ、そうだったね。そういう形だった。この公式をパッと出せる方法はないかな?
語呂合わせとか覚え方ならいっぱいあると思うけど、物理はやっぱり、公式をいつでも導出できるくらい、原理に通じていないとダメだと思う。
う〜ん、耳がイタイ。
じゃあさ、せっかくだから、ようこちゃんやってみてよ!
ドップラー効果を? そうだねぇ、じゃあやろうか。ちなみに、ドップラー効果そのものが「相対的」な効果だってことに気づいてる?
ん? どういう意味?
つまりさ、音とか光っていうのは「誰から聞くか(見るか)」によって全く別物だっていうことだよ。ドップラー効果の例だと、救急車のサイレンの音がよく使われるけど、例えば救急車が近づいてくる人と救急車が遠ざかる人とでは、そのサイレンの音は全く違うものなんだ。光も同じなんだけど、光速が速すぎるせいで、その違いに気づいていないんだね。
相対的っていうのはそういうことだね。もし、音が絶対的なら誰から聞いてもおなじだもんね。
そう! だから、ドップラー効果を考えるときには、「観測者からその音源を聞いたり、光源をみたりすること」が本質的なんだ。物理の言葉で言うと、静止した物体に従う実験室系じゃなくて「観測者に従う慣性系」でみた方がいい、ってことなんだ。そして、どの系でみても結果は同じというのがアインシュタインが考えた相対論の教えなんだけどね。
要は、相対速度とかを考えろってこと?
いいセンス! その通り。ドップラー効果の原理を考えるときは相対速度が欠かせない考え方だよ。じゃあ、本題に戻るよ。たぶん、図があった方がいいと思うから描いてみるね。
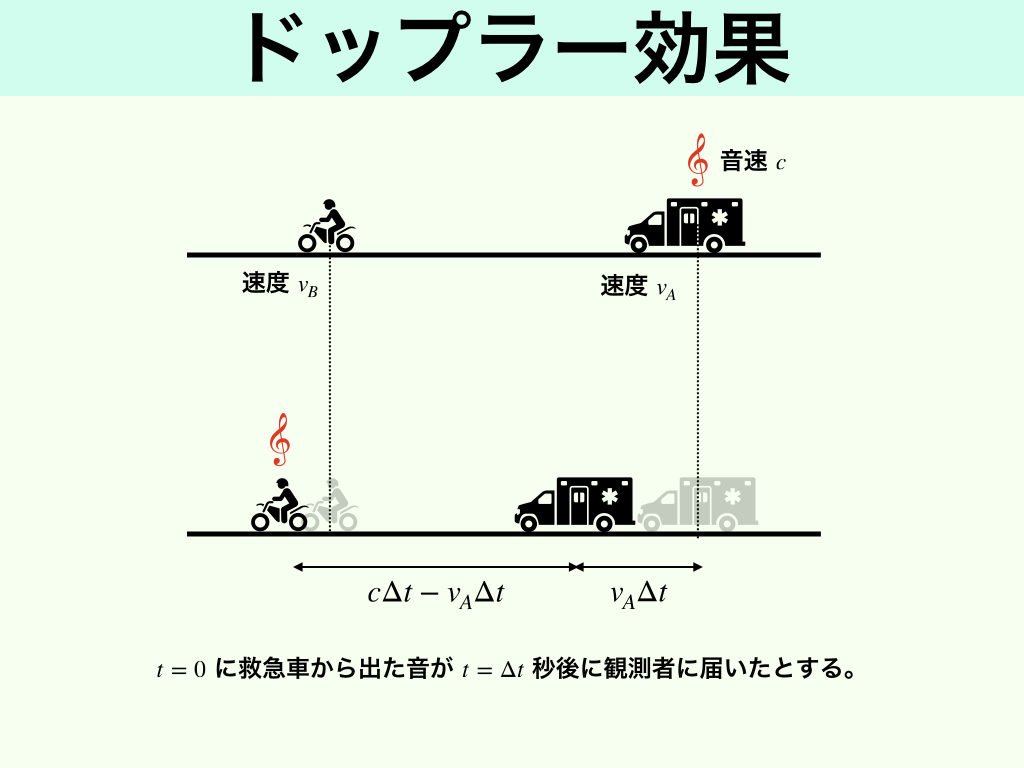
こういう状況を考えるよ。ちなみにベクトルの向きは救急車から観測者への向きを正とするよ。この図のように、観測者と救急車までの距離は、\(c\Delta t – v_{A}\Delta t\)のように書けるってこと、観測者の速度によらずに書けるというのが重要だね。
じゃあ、観測者と救急車までの距離の間に、何個の波が出ているかわかる?
静止した観測者にとっての救急車の振動数を\(f_{A}\)とすると?
振動数っていうのは、単位時間あたりの波の数だから、時間をかければ波の数になる、ってことは
\(f_{A}\Delta t\)個だね。あ、ごめん、まみちゃん。
そう、正解。距離と波の数がわかっているなら、そこでの波長は簡単に求められるよね。
$$\lambda_{B} = \frac{c\Delta t – v_{A}\Delta t}{f_{A}\Delta t} = \frac{c – v_{A}}{f_{A}}$$
あとは、これを振動数に変換するんだけど、ここで重要なのは、「観測者にとっての音」を考えているってことだよ。だって\(f_{B}, \lambda_{B}\)っていうのは観測者が聞く音の振動数とか波長なんだから、当然、音の速度も観測者にとっての「相対速度」じゃないといけない。すると?
今度は譲らないよ。相対速度はようこちゃんに教わったからね。
答えは\(c-v_{B}\)だよ。
そうだね。だから観測者が聞く音の振動数は
$$f_{B} = \frac{c-v_{B}}{\lambda_{B}}$$
で求まる。これをさっきの式に代入すれば、さっき、えりが言ってくれたように
$$f_{B} = \frac{c-v_{B}}{c-v_{A}}f_{A}$$
が出てくるんだね。今は無風だと思っているけど、もし風が吹いているという条件なら相対速度の部分が変わって、\(c+\omega-v_{B}\)みたいにすればいいんだよ。\(\omega\)が風の速度だね。
お〜、なんか簡単に求められるんだね。
そうだよ。大学によっては、ドップラー効果の導出を出題してくるところも多いから、こういう考え方は重要。
さて、そろそろ本題に戻ろうか。
え〜と、どういう問題だっけ?
今までようこちゃんが解説してくれたものと原理的にはおなじ状況だね。近似を使わないなら、求める答えは
$$f_{B} = \frac{c-v_{B}}{c-v_{A}}f_{A}$$
でいいと思うんだけど、誘導をみると、近似を使えって言っているよね。
そう。だから、この式を近似式を使って変形する必要があるんだ。
よ〜し、それはあたしがやるね。
$$\begin{eqnarray}
\frac{f_{B}}{f_{A}} &=& \frac{c-v_{B}}{c-v_{A}}\\
&=& \frac{1-\frac{v_{B}}{c}}{1-\frac{v_{A}}{c}}\\
&=& \left(1-\frac{v_{B}}{c}\right)\left(1+ \frac{v_{A}}{c}\right)\\
&=& 1- \frac{v_{B}}{c} + \frac{v_{A}}{c}\\
&=& 1+ \frac{v_{A}-v_{B}}{c}
\end{eqnarray}$$
最初は分母・分子を\(c\)で割る。2~3行目は1つめの近似式、3~4行目は2つめの近似式を使っているんだね。
うん、まみの答えで正解。(あ)は
$$\frac{v_{A}-v_{B}}{c}$$
だね。最初から二つの近似を使ったね。ウォーミングアップって感じかな。
数学と違って問題文が長いから、それを読むのも大変だよ。
今日は、問題を解くだけじゃなくて、じっくり「読む」からね。まだまだ先は長いよ。じゃ、次のステップ。
問題 (1) – 2 波から時間へ
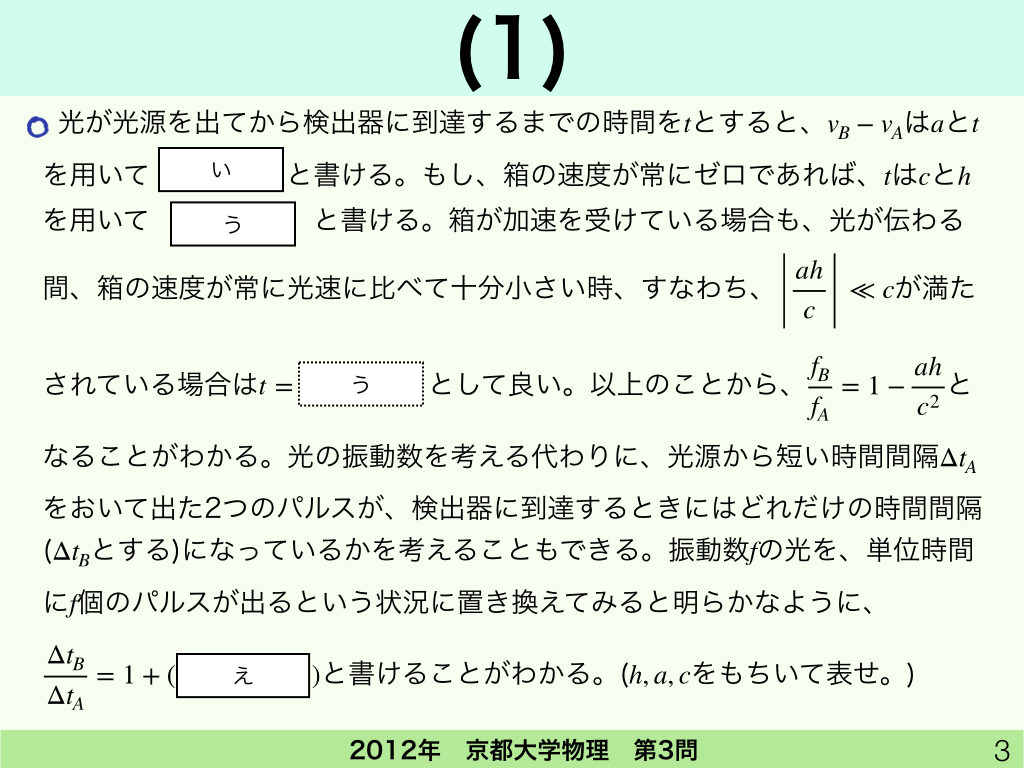
ここはすんなり読めるかな? 二人は、等加速度運動の公式はばっちり? 少なくともまみは大丈夫だよね。
多分。ようこちゃんが色々教えてくれたから、大丈夫だと思う。
わたしも平気だと思うよ。
よし、じゃあ、問題を解いてみよう。
等加速度運動しているなら、公式を使うと
\(v_{B} = v_{A}+at\)なんだから\(v_{B} – v_{A} = at\)だよね。「う」なんて距離割る時間をすればいいんだから、\(t= \frac{h}{c}\)だし。
ちなみに、問題にはなっていないけど、自分たちで今までの答えから\(\frac{f_{B}}{f_{A}}\)を求めてみると?
見なおしってことだね。
$$\frac{f_{B}}{f_{A}} = 1+ \frac{v_{A}-v_{B}}{c}$$
だからここに値を代入すると
$$\frac{f_{B}}{f_{A}} = 1- \frac{ah}{c^{2}}$$
となってたしかに一致するね。
そう。誘導問題ならではの確認作業だね。虫食いは一つでも間違えるとそれ以降もボロボロ間違えるから、こういう確認はとても大事だよ。さて、最後の「え」は大学の教科書によく登場する「明らかな」問題だね。大学の教科書にはよく、「容易に」とか「自明に」とかが付いていて、読者からしたら全然「容易」でも「自明」でもないことがあるんだけど、この問題はどう?
重要なのは、「何が等しいか」ってことかな?
この場合は、光源から\(\Delta t_{A}\)に出た波の数と検出器で\(\Delta t_{B}\)の間に出た波の数が等しいという式をたてればいいんだよね。
え〜と、そうすると、
$$f_{A}\Delta t_{A} = f_{B} \Delta t_{B}$$
という式が成り立つから
$$\frac{f_{B}}{f_{A}} = \frac{\Delta t_{A}}{\Delta t_{B}}$$
という変換式になるよ。つまり、右辺は逆数だね。
$$\frac{\Delta t_{B}}{\Delta t_{A}} = \frac{1}{1- \frac{ah}{c^{2}}}$$
また近似が使えるから
$$\frac{\Delta t_{B}}{\Delta t_{A}} = 1+ \frac{ah}{c^{2}}$$
が答えだ。
二人ともいい感じ。まとめると「い」、「う」、「え」の答えはそれぞれ
$$at,\ \frac{h}{c},\ \frac{ah}{c^{2}}$$
だね。
ところで、この問題で、話が振動数(波の数)から時間に切り替わったよね。この切り替えがとても重要だよ。京都大学ではこうやって基本的な事柄を連続的に別のテーマに置き換えていって、壮大なスケールの話をする方向に持っていくから、うまくそれについていけると、本当に解いていて面白い問題なんだ。
うん、それはわかるかも。東京大学の物理とはそこが違うよね。なんか、講義を受けている感じがするもん。
うん、その感覚で問題を解くのがいいと思うよ。問題を解く以上に学べることがたくさんあると思う。例えば、箱の速度が問題文中の条件に従うと、なぜ時間を近似できるのかっていうことも自明ではなくて、「2次以上の微小量」を無視するという原理に従っているんだ。ほとんど数学だから、まみ、計算してみる?
え? あたし?
じゃあ、途中までわたしがやるね。近似をしないで考えると、時間と速度の関係はこうなってる。
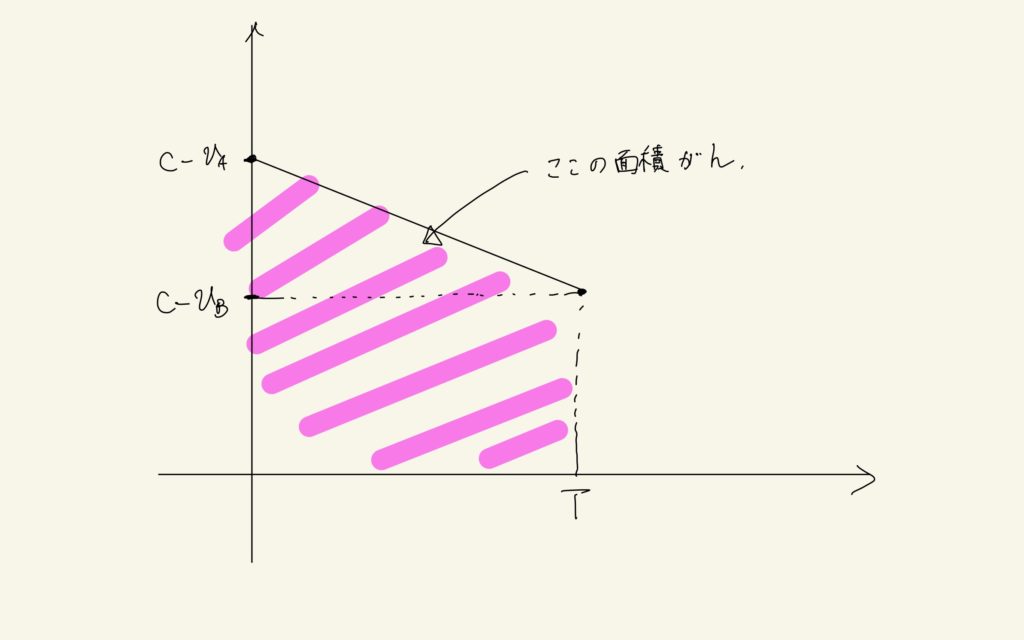
そうすると\(T\)を求める式は、
$$\frac{1}{2}(c-v_{B}+c-v_{A})\times T = h$$
計算して整理すると
$$aT^{2}-2(c-v_{A})T+2h =0$$
ってなる。まみちゃん、あとは任せた!
これを計算してTを求めればいいんだね。
$$T = \frac{(c-v_{A})\pm\sqrt{(c-v_{A})^{2}-2ah}}{a}$$
ここで微小量を作り出すのがポイント。
$$T = \frac{c-v_{A}}{a}\left(1\pm \sqrt{1-\frac{2ah}{(c-v_{A})^{2}}} \right)$$
ここで
$$\frac{2ah}{(c-v_{A})^{2}} = \frac{2ah}{c^{2}}\times\frac{1}{ 1-\frac{v_{A}^{2}}{c^{2}} }$$
で2次の微小量を無視すると、
$$\frac{2ah}{(c-v_{A})^{2}} = \frac{2ah}{c^{2}}$$
ここで問題文の条件として
$$|\frac{ah}{c}| \ll c$$
を仮定すると
$$\frac{2ah}{(c-v_{A})^{2}}$$
は1に対して微小であると考えられる。そこで、前の式に戻って、
$$\begin{eqnarray}
T &=& \frac{c-v_{A}}{a}\left(1\pm \sqrt{1-\frac{2ah}{(c-v_{A})^{2}}} \right)\\
&\simeq& \frac{c-v_{A}}{a}\left( 1 \pm \left( 1 – \frac{ah}{(c-v_{A})^{2}} \right)\right)
\end{eqnarray}$$
ん? まみちゃん、最後の近似はどこから?
あ、ごめん。これは、
$$f(x) = \sqrt{1-x}$$
の\(x=0\)周りの近似式でね、1次までを考えると
$$f(x) \simeq 1-\frac{1}{2}x$$
で表せるんだよ。さっきと同じように、テーラー展開から求められるよ。
うん、物理ではよく使う近似式だから覚えておくといいかも。と言っても、京都大学でも、これを使うなら、問題文に紹介されているけどね。
そっか。ありがと。そういえば、見たことあるかも。
じゃあ、続けるね。
$$T \simeq \frac{c-v_{A}}{a}\left( 1 \pm \left( 1 – \frac{ah}{(c-v_{A})^{2}} \right)\right)$$
からは二つの答えが考えられるけど、ここでの条件では「マイナス」を取らないといけないよ。理由は、たぶん、えりかちゃんが知ってる。
え? いきなり振る?
え〜と、図の台形の面積が\(h\)になる時間は、たしかに二つあって箱の速度が正のときか、負のとき。「プラス」の方が箱の速度が負になるときだけど、今考えている状況では、そういうのを考えていないから「マイナス」の方を取らないといけない、ってことかな?
そうだね。そもそも物体の速度は「光速を超えない」という原理があるから、どのみちそういう場合は起こりえないけどね。
それで、マイナスの方をとると
$$T \simeq \frac{h}{c-v_{A}}$$
となる。感覚だと「\(c\)は\(v_{A}\)よりもはるかに大きいから」って言って\(v_{A}\)を消しちゃうけど、それはもちろんダメ。今使っていいのは、2次以上の微小量を無視するって原理だけだからね。
$$T \simeq \frac{h}{c}\times \frac{1}{1-\frac{v_{A}}{c}}$$
として、問題文の近似を使うと
$$T \simeq \frac{h}{c} + \frac{hv_{A}}{c^{2}}$$
が出てくる。で、この第2項が2次の微小量だから無視できて
$$T \simeq \frac{h}{c}$$
となる。問題文は1行で済ませているけど、かなり大変だよね。
それを言いたかった。大学の教科書なんか、ある1行を読むのに何時間もかかることがあるんだよね。京都の問題も「ちゃんと」読もうとしたら本当に大変だよ。さて、じゃあ、次の問題行くよ。
問題 (2) – 1 アインシュタインの等価原理

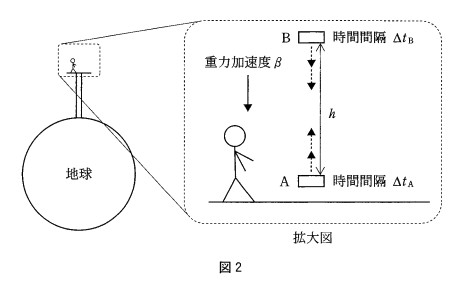
問題自体は全然難しくないけど、本質的には非常に重要なことを言っている箇所だね。特殊相対論から一般相対論への架け橋となった原理だよ。原理とついていることからわかる通り、今のところ、これを証明する方法は実験的検証しかない。数学的な式から、この原理は証明されるんじゃなくて、いろんな実験をしてこの原理が覆る状況がない、という事実から認められたものなんだね。
問題としてはたしかにかんたんかも。最初は慣性力、次は向きが重要で\(-a\)だよね。
そう、正解。(お)は慣性、(か)は\(-a\)だね。等価原理について話すとそれだけで何日もかかるから、ここではさすがに置いとくよ。でも、この等価原理を持ち出すと、今までとほとんど同じテーマを扱いながら、ガラリとその景色が変わるから、そこに注意してね。

さぁ、いよいよ地球が登場したね。万有引力を考えるよ。
物体と地球との万有引力は地球からずっと離れた遠方方向への向きを正ととると
$$F = -\frac{GMm}{r^{2}}$$
で表せたよね。今重力加速度を\(g\)とすると
$$mg = -\frac{GMm}{r^{2}}$$
が成り立つから
$$g = -\frac{GM}{r^{2}}$$
となるね。だから、大きさは、\(\frac{GM}{r^{2}}\)で向きは地球の中心方向ってことかな。
うん、完璧。この計算はよくやるから慣れちゃうよね。それで、アインシュタインの等価原理を考えると、重力がある状況での物理現象は、重力がなく加速度運動をしている状況での物理現象と区別がつかない、つまり、同じだということを言っているんだよ。それで、それを使って重力がある状況での考察に移っているんだね。
あ、そうか。その後の問題はいわゆる似ている現象の「当てはめ」問題なのかぁ。重力がある状況では下向きに、大きさ\(\beta\)の重力加速度がある、ってことは、重力加速度は\(-\beta\)だけど、これって、さっきの状況で\(-a\)だったのと全く同じだ。だから\(a\)を\(\beta\)に当てはめるだけだから
$$\frac{\Delta t_{B}}{\Delta t_{A}} = 1+ \frac{\beta h}{c^{2}}$$
なのかな。
いいねぇ、二人ともちゃんとついてきている感じ。そういうこと。
この問題では(き)が地球の中心方向, (く)、(こ)はそれぞれ
$$\frac{GM}{r^{2}},\ \frac{\beta h}{c^{2}}$$
ってことだね。さぁて、ここからが面白くなってくるところだよ。
問1

問題文が言っていることがすごく面白いよ。重力があるところでは、時間の進み具合が違うって言ってる。ここまでの流れが本当に巧みだと思う。まず、受験生に馴染みの深いドップラー効果の式を使わせて、それを時間間隔に変換する。その後、アインシュタインの等価原理を使って、加速度運動している状況を重力がある状況に持ってきて議論している。
たしかにね、ちょっと面白いかも。でも、この問題は?
あ、わたし、これできそう。
さっきまみちゃんがやったようなことと同じことをすればできそうだもん。
BからAへ光を送るってことは、重力加速度が上向きで、同じ大きさ\(\beta\)の状況をまず考える。そうすると、今度は最初の状況と比べて\(a = -\beta\)とした場合と同じだから、
$$\frac{\Delta t_{A}}{\Delta t_{B}} = 1+ \frac{-\beta h}{c^{2}}$$
だよね? それで、これを逆数にすると
$$\frac{\Delta t_{B}}{\Delta t_{A}} = \frac{1}{1- \frac{\beta h}{c^{2}}}$$
になるから、近似の式を使ってあげて
$$\frac{\Delta t_{B}}{\Delta t_{A}} = 1+ \frac{\beta h}{c^{2}}$$
ほら、もどった。
うん、そうそう。結局当てはめでできちゃうよね。
さて、ここからさらに新しい概念が導入されるよ。
問題 (3)-1 重力ポテンシャルの導入

重力ポテンシャル、なんて聞いたことないと思うけど、言っていることは難しくないよ。問題文のいう通りに考えれば、自然とついていける。
たしかに、そうだね。Aの高さを基準にとると、Bでの位置エネルギーは\(m\beta h\)だから重力ポテンシャルは\(A=0, B=\beta h\)となって
$$\phi_{B}-\phi_{A} = \beta h$$
となるね。そうすると、その後の問題もすぐできて、
$$\frac{\Delta t_{B}}{\Delta t_{A}} = 1+ \frac{\beta h}{c^{2}} = 1+ \frac{\phi_{B} – \phi_{A}}{c^{2}}$$
なのかな。
正解!(こ)、(さ)はそれぞれ
$$\beta h,\ \frac{\phi_{B} – \phi_{A}}{c^{2}}$$
だね。ポイントは、この問題文の最後の1文だよ。「この式は重力加速度が空間的に一様でなくても成り立つ」というところ。この確認が実はまた大事で、実際の宇宙では、場所によって重力加速度は異なってしまうから、もし重力加速度が空間的に一様な場所でしか成り立たないなら、この理論は対して実用的じゃないけど、ある条件を満たす限り、かなり実用的な式だってことだね。
これはどうやって確認できるの?
いい質問だね。答えはこうだよ。
問2

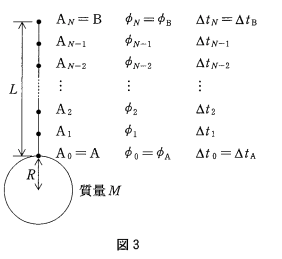
ある区間を微小区間に分けて考えるという、微積分学の常套手段だね。同じような考え方は、「万有引力」から「万有引力の位置エネルギー」を求める時にも使っているよ。この問題はまみが得意、かな?
うん、そうだね。これはできると思うよ!
とりあえず、各区間の式を書いていくと
$$\begin{eqnarray}
\frac{\Delta t_{1}}{\Delta t_{0}} &=& 1+ \frac{\phi_{1}-\phi_{0}}{c^{2}}\\
\frac{\Delta t_{2}}{\Delta t_{1}} &=& 1+ \frac{\phi_{2}-\phi_{1}}{c^{2}}\\
\cdots\cdots\\
\frac{\Delta t_{N}}{\Delta t_{N-1}} &=& 1+ \frac{\phi_{N}-\phi_{N-1}}{c^{2}}\\
\end{eqnarray}$$
だから、いわゆるへんぺんのかけ合わせで、左辺はバシバシ消えていくから
$$\frac{t_{N}}{t_{0}} = \left(1+ \frac{\phi_{1}-\phi_{0}}{c^{2}}\right)\left(1+ \frac{\phi_{2}-\phi_{1}}{c^{2}}\right)\cdots\cdots\left(1+ \frac{\phi_{N}-\phi_{N-1}}{c^{2}}\right)$$
それで、2つめの近似式を用いると
$$\frac{t_{N}}{t_{0}} = 1+\frac{\phi_{1}-\phi_{0}}{c^{2}}+\frac{\phi_{2}-\phi_{1}}{c^{2}}+\cdots\cdots+\frac{\phi_{N}-\phi_{N-1}}{c^{2}}$$
となってこれもバンバン消えていくから残るのは
$$\frac{t_{N}}{t_{0}} = 1+\frac{\phi_{N} – \phi_{0}}{c^{2}}$$
ここで、添え字が0は\(A\), \(N\)は\(B\)を表すので
$$\frac{t_{B}}{t_{A}} = 1+\frac{\phi_{B} – \phi_{A}}{c^{2}}$$
となる。
さすが、まみ。こういう問題はお手の物だね。この問題で今までの事実が、ある条件下で、万有引力が各地点で異なる宇宙空間でも成り立つことがわかったね。そこで、舞台は一旦宇宙空間に移るよ。
問題 (3)-2 宇宙空間への拡張

時間のズレを、宇宙空間で考える時がきたね。さぁ、この問題はどう。
重力の位置エネルギーは、万有引力を積分することで得られるから
$$-\frac{GMm}{r}$$
だね。それで、\(\phi_{A}\)を求める時に注意しないといけないのは、記号だよね。地点\(A\)での半径は今、\(R\)になっているから位置エネルギーは、
$$-\frac{GMm}{R}$$
と書く必要があって、重力ポテンシャルは\(m\)に比例する部分の
$$-\frac{GM}{R}$$
$$g = \frac{GM}{R^{2}}$$
を使って表すなら
\(\phi_{A} = -gR\)
となる。最後の代入は、まみちゃん!
えりちゃん、そのままやってくれればいいのに!
$$\begin{eqnarray}
\phi_{B}-\phi_{A} &=& -g\frac{R^{2}}{R+L}+gR\\
&=& g\frac{RL}{R+L}\\
\frac{\Delta t_{B}}{\Delta t_{A}} &=& 1 + g\frac{RL}{c^{2}(R+L)}\\
\end{eqnarray}$$
かな?
二人ともバッチリ、誘導に乗れてるね。結局(し)、(す)、(せ)は
$$-\frac{GMm}{r},\ -gR,\ g\frac{RL}{c^{2}(R+L)}$$
だね。これで最後の準備が整ったよ。いよいよクライマックスだ!
問題 (4)-1 人工衛星の時計の進み方

ここで、話はそのまま宇宙つながりで人工衛星に移っているね。時計の進み方の違いを、実際に導入されているGPSを例に理解させようとしている。高校物理+\(\alpha\)でここまで誘導してくれるのは、やっぱり、京都大学ならではって感じがするよね。おまけに、特殊相対論まで登場しているんだから。
ねぇ、ちょっと気になったんだけど、今までの時計の進み方の違いと、特殊相対論での時計の遅れっていうのは違う話なの? それとも同じ話?
まみ、いいところに気づいたね。結果としては時計の進み方に違いが生じるっていう似たような話だけど、中身は全然違うよ。今まで議論してきた時計の進み方の違いというのは、「重力下または加速度運動をしている物体」が感じるものだった。つまり、その根元は「加速場」「重力場」というところにある。でも特殊相対論では、運動をしている物体(加速していなくても)と静止している物体との間に生じる時間の進み方の違いを言っているんだ。特に、特殊相対論ではその物体が光速に近ければ近いほど、静止している物体に対して、時計の遅れ方が遅くなる。
光速に近い速さで動いている物体ほど、静止している物体よりも寿命が長いってこと? 時計の進み方が遅れるっていうのは、寿命が延びるってことだよね。
うん、でもそういう意味では、光速でなくても動いてさえいれば時計の進み方は遅れるよ。ただ、速度が小さいほど、その効果はほとんど無視されちゃうほど小さいけどね。
具体的には、どのくらい延びるの? 例えばあたしがずっと走り続けたとしたらどう?
聞きたい?
静止している物体の時計の進みを\(\Delta t\), まみの時計の進みを\(\Delta t^{\prime}\)とすると、「ローレンツ変換」というものを使って
$$\Delta t^{\prime} = \sqrt{1-\frac{v^{2}}{c^{2}}}\Delta t$$
という関係があるよ。
今、まみの走る速さを\(10 \mathrm{km/h}\), つまり、だいたい\(3 \mathrm{m/s}\)だとすると、光速は\(c \simeq 3.0\times10^{8}\)だから
$$\sqrt{1-\frac{v^{2}}{c^{2}}} \simeq 1 – \frac{1}{2}\frac{1}{10^{16}}$$
となって、この
$$\frac{1}{2}\frac{1}{10^{16}}$$
の分だけ寿命が延びるってこと。
うわ、これはほとんど誤差みたいなもんだね。
わかった。じゃあ例えば飛行機だとどう?
飛行機か。飛行機でもせいぜい、音速程度、つまり\(300 \mathrm{m/s}\)くらいが限界だから、
$$\frac{1}{2}\frac{1}{10^{10}}$$
くらいの違いかな。ただ、このくらいになると実際に原子時計の遅れとして観測できるようになるよ。飛行機に乗っている人は、ごくごくわずかだけど寿命が延びているんだね。特殊相対論の効果が大きく聞いてくるのは、私たちの体を作る根元、素粒子の世界の話だよ。
素粒子って、陽子とか電子?
電子は素粒子だけど、陽子はもっと細かくなる。クォークっていう粒子があるからね。
うん。でも、陽子も条件次第では光速に近い速度で運動することがあるよ。時には光速の99%程度の速さで動くことがある。このときの時間の遅れは
$$\Delta t^{\prime} = \sqrt{1-0.99^{2}}\Delta t$$
だから
$$\Delta t^{\prime} = \sqrt{1-0.99^{2}}\Delta t \simeq 0.14\Delta t$$
となって、静止しているときの7倍くらい寿命が延びるんだよ。
すごいね、相対論!
この問題は結果を使っているだけだけど、大学に入るとアインシュタインの思考を辿りながら、特殊相対論も学べるし、それを使ってもっと面白い話ができるんだよ。
ようこちゃん、大学生じゃないじゃん! 本当に物理好きなんだね。
まぁね! じゃあ問題解いていこうか。
この問題は遠心力を使うだけかな。人工衛星は等加速円運動をしているから、人工衛星から見たときの遠心力と万有引力が釣り合うから
$$m\frac{v^{2}}{R+L} = mg\frac{R^{2}}{(R+L)^{2}} $$
$$v^{2} = g\frac{R^{2}}{R+L}$$
だね。これを使うと
$$\frac{\Delta t_{C}}{\Delta t_{B}} = 1 – g\frac{R^{2}}{2c^{2}(R+L)}$$
そう。だから、(そ)は
$$\frac{gR^{2}}{2c^{2}(R+L)}$$
が正解ってことだね。次の問題がラストだよ。
問3

これは、さっき私たちが計算したように、どれくらい時間の進み方が違うのかを実際の数値で考察させる問題だね。今までの答えがあっているなら、あとはただただ、割り算とかけ算をしていくだけ。
じゃあ、まず
$$\frac{\Delta t_{B}}{\Delta t_{A}} = 1 + g\frac{RL}{c^{2}(R+L)}$$
を求めるよ。
$$\begin{eqnarray}
\frac{\Delta t_{B}}{\Delta t_{A}}
&=& 1 + \frac{9.8\times6.0\times3.0}{9\times(3.6)}\frac{10^{13}}{10^{23}}\\
&=& 1 + \frac{19.6}{3.6}\times10^{-10}\\
&=& 1 + 5.4\times10^{-10}
\end{eqnarray}$$
次に
$$\frac{\Delta t_{C}}{\Delta t_{B}} = 1 – g\frac{R^{2}}{2c^{2}(R+L)}$$
を求めるよ。
$$\begin{eqnarray}\frac{\Delta t_{B}}{\Delta t_{A}}
&=& 1 – \frac{9.8\times6.0\times6.0}{2\times9\times(3.6)}\frac{10^{12}}{10^{23}}\\
&=& 1 – \frac{19.6}{3.6}\times10^{-11}\\
&=& 1 – 5.4\times10^{-11}
\end{eqnarray}$$
じゃあ、最後はわたし。
まみちゃんの出してくれた答えを見ると、
$$\frac{\Delta t_{C}}{\Delta t_{B}}, \frac{\Delta t_{B}}{\Delta t_{A}}$$
はどちらも1に対して微小量だから近似が使えるね。
$$\begin{eqnarray}
\frac{\Delta t_{C}}{\Delta t_{A}} &=& \frac{\Delta t_{B}}{\Delta t_{A}} \times \frac{\Delta t_{C}}{\Delta t_{B}}\\
&=& \left( 1 + g\frac{RL}{c^{2}(R+L)} \right)\left( 1 – g\frac{R^{2}}{2c^{2}(R+L)} \right)\\
&\simeq& 1 + g\frac{RL}{c^{2}(R+L)} – g\frac{R^{2}}{2c^{2}(R+L)} \\
&=& 1 + g\frac{R(L-R)}{c^{2}(R+L)}\\
&=& 1 + 5.4\times10^{-10} – 5.4\times10^{-11}\\
&=& 1 + 4.9\times10^{-10}\\
\end{eqnarray}$$
は〜、どうだろう?
二人ともお見事、正解!
全てのストーリーを味わい尽くしたね。
数学の問題、6問くらい解くのと同じくらい疲れたよ。
やっぱり、物理は大変だよ。
でも、一つ一つは難しくないし、誘導は丁寧だから、解いていて楽しかったよ。
そう言ってもらえるとなんか、嬉しい。
やっぱり、この問題を入試問題として解くだけじゃ、もったいないよね。
えりかちゃん、今度は数学も一緒にやろうよ!
うん、いいよ。こないだ、研究会してたでしょ。ほんとはわたしもやりたかったんだ!
またすぐやるよ、ねぇ、ようこちゃん。
え? う、うん。そうかなぁ?
今日は楽しかったよ。どうもありがとう、二人とも。
どういたしまして!



コメント