自問
東京大学2001年数学第1問は次のような問題でした。
問題
半径rの球面上に4点ABCDがあり、\(AB=\sqrt{3}, AC=AD=BC=BD=CD=2\)を満たしている。このとき\(r\)を求めよ。この問題には初等幾何、ベクトル、座標設定、どれを使っても解けます。ここでは、初等幾何とベクトルを使った時のメリット、デメリットは何か考えてみました。
自答
初等幾何を用いた回答
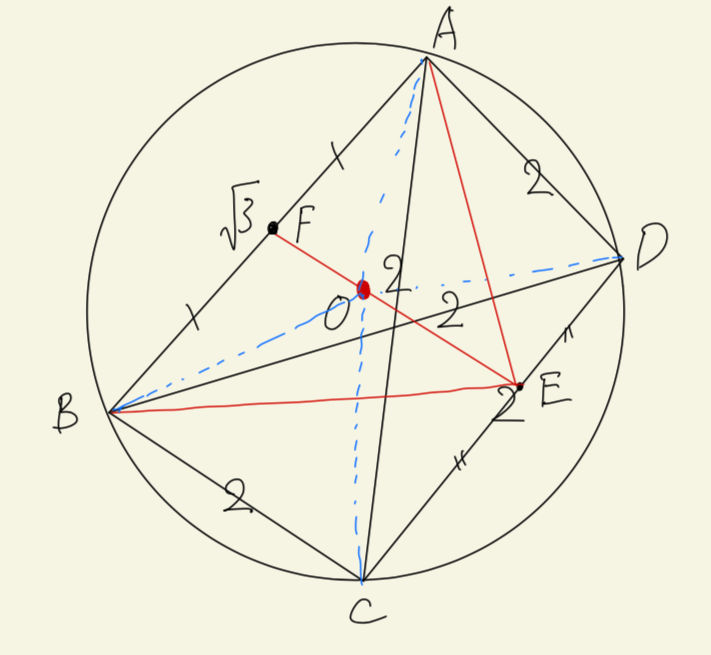
上の図のように記号を定義します。初等幾何では、辺の値関係から空間の位置関係を把握していくことがとても重要です。この場合は次のことに気づければ寄り、です。
空間の位置関係
外接球の中心Oは三角形ABE上にあり、かつEF上である。$$EF = OE + OF$$
という関係が成り立つことがわかります。三角形ABEは正三角形で、三角形OEC, 三角形OFAで三平方定理を使うと
$$EF = \frac{3}{2},\ OF = \sqrt{r^{2}-\frac{3}{4}},\ OE = \sqrt{r^{2}-1}$$
より、rについて解くと
$$r = \frac{\sqrt{13}}{3}$$
と求めることができます。
このように初等幾何を用いるなら、平面図形で考えて「気づき」を得て数式を作っていくことが鍵となります。
ベクトルを用いた解法
さて、ベクトルを用いて解くこともできます。ベクトルの破壊力は、「気づき」を一切必要としないところにあります。すなわち、ベクトルを設定してしまえば、あとはただただ代数計算をこなしていけば、自然と答えを得ることができるのです。ただ、問題とベクトルの設定の仕方によっては膨大な計算量を強いられることがありますので、注意が必要です。
ここでは、\( \overrightarrow{AB} = \vec{b},\ \overrightarrow{AC} = \vec{c},\ \overrightarrow{AD} = \vec{d}\)と設定して問題を解きます。計算量は、入試現場において解くことを前提としたとき、僕の中ではギリギリ許容量でした。
空間ベクトルの性質から3つの実数(m, n, k)を用いて
$$\overrightarrow{AO} = m\vec{b} + n\vec{c} + (k-m-n)\vec{d}$$
と表せます。教科書に載っているものは、第3項目の係数が(1-m-n)となるものですが、今はOが平面BCD上にあるとは限らない(というか、ない)ので、(k-m-n)としています。これを使うとベクトルBO, CO, DOも同様に
$$\overrightarrow{BO} = (m-1)\vec{b} + n\vec{c} + (k-m-n)\vec{d}$$
$$\overrightarrow{CO} = m\vec{b} + (n-1)\vec{c} + (k-m-n)\vec{d}$$
$$\overrightarrow{DO} = m\vec{b} + n\vec{c} + (k-m-n-1)\vec{d}$$
と表せます。あとは、半径がrであるという事実を使えば、
$$|m\vec{b} + n\vec{c} + (k-m-n)\vec{d}|^{2} = r^{2}$$
$$|(m-1)\vec{b} + n\vec{c} + (k-m-n)\vec{d}|^{2} = r^{2}$$
$$|m\vec{b} + (n-1)\vec{c} + (k-m-n)\vec{d}|^{2} = r^{2}$$
$$| m\vec{b} + n\vec{c} + (k-m-n-1)\vec{d}|^{2} = r^{2}$$
というように式が4つできますね。未知定数も4つなので、原理的には解けるはずです。そして、実践的にもこの形は解けます。これらを解く準備としては以下の内積を計算しておく必要があるでしょう。
$$\vec{b}\cdot\vec{c} = \vec{b}\cdot\vec{d} = \frac{3}{2}$$
$$\vec{c}\cdot\vec{d} = 2$$
これは簡単に求められます。さて、先ほどの4つの式を上から順に式1, 2, 3, 4とします。これらを一生懸命計算すると次のようになります。
$$3m^{2}+4n^{2}+4(k-m-n)^{2}+3mn+3m(k-m-n)+4n(k-m-n) = r^{2}$$
$$3(m-1)^{2}+4n^{2}+4(k-m-n)^{2}+3(m-1)n+3(m-1)(k-m-n)+4n(k-m-n) = r^{2}$$
$$3m^{2}+4(n-1)^{2}+4(k-m-n)^{2}+3m(n-1)+3m(k-m-n)+4(n-1)(k-m-n) = r^{2}$$
$$3m^{2}+4n^{2}+4(k-m-n-1)^{2}+3mn+3m(k-m-n-1)+4n(k-m-n-1) = r^{2}$$
グッと睨むと、式1を支点にして引き算をすれば、半分程度の項がそのまま消えることが見えてきます。つまり、式1-式2, 式1-式3, 式1-式4などと計算すれば割とスッキリするのです。以下に計算した結果を挙げます。
式1-式2
$$m+k=1$$式1-式3
$$4n-m+4k=4$$式1-式4
$$8k-5m-4n=4$$$$k = \frac{7}{9},\ m = \frac{2}{9},\ n = \frac{5}{18}$$
です。ゆえにAOベクトルは
$$\overrightarrow{AO} = \frac{2}{9}\vec{b} + \frac{5}{18}\vec{c} + \frac{5}{18}\vec{d}$$
です。最後はこのベクトルの大きさを求めれば、それが求める半径です。
$$|\overrightarrow{AO}|^{2} = \frac{1}{18^{2}}|4\vec{b} + 5\vec{c} + 5\vec{d}|^{2}$$
$$|\overrightarrow{AO}|^{2} = \frac{1}{18^{2}}\times468 = \frac{13}{9}$$
$$|\overrightarrow{AO}| = r = \frac{\sqrt{13}}{3}$$
より、初等幾何での答えと一致しましたね。
初等幾何とベクトルでの比較
この問題だけで一般化することは危険ですが、僕の経験上では初等幾何のメリット・デメリット、ベクトルのメリット・デメリットは次のようなものではないでしょうか。
初等幾何
デメリット:補助線を引きながら、新しい情報を次々とあばき出し、必要な辺の長さや角度を求めていく知恵と経験が必要である。メリット:計算式が容易で計算量が少ない。低学年でも解ける。
ベクトル
デメリット:計算量が増加することが多い。メリット:知恵と経験などなくても「計算能力」とベクトルの計算に慣れていれば解ききれる。
初等幾何は「スマート」、ベクトルは「マッチョ」とも言い換えられるでしょうか。とはいえ、問題に応じて、ベクトルの方が計算量が少なくて済む場合もあるので、必ずしも上のように一般化できるわけではありません。あくまでそういう傾向があるなぁ、と思います。では、座標設定はどうなのでしょうか。機会があれば、座標設定とも比較してみたいです。

コメント