今、雨が降り始めたんだ。濡れちゃった。
まみちゃん、何で、顔までそんなに濡れてるの? 傘ささなかったの?
差してたよ。自転車に乗りながら。
もしかして、傘、真上に差してた?
え? うん。
それだね。じゃあ、今日は傘の物理でもやろっか。
$$v_{rel} = v_{2}-v_{1}$$
よくわかんないなぁ。
じゃあ、次の図は?
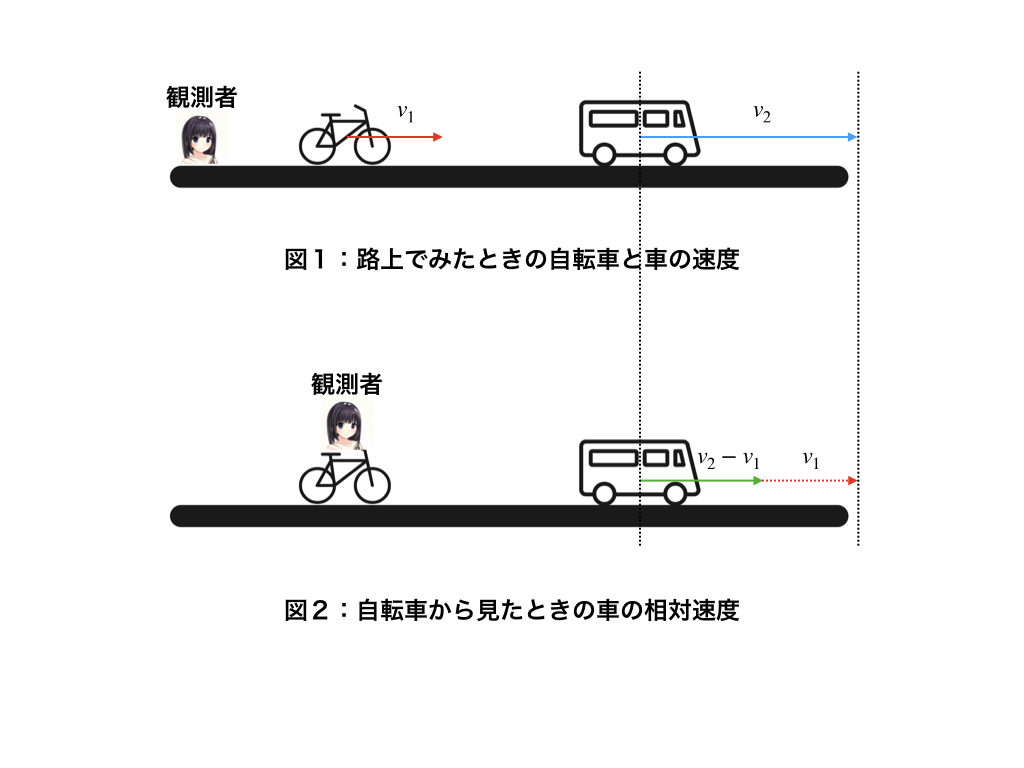
図1では、路上で見たときの自転車と車の速度の関係性を表しているよ。このとき観測者は路上にいるね。観測者を自転車に乗っている人にずらして見ると、同じ方向に走っている車は少し遅くなって見えるんじゃないかな。
その、遅くなった速度というのが、相対速度、ってこと?
そうそう。物体Aの相対速度というのは、観測者をずらして見たときの、物体Aの速度ってことなの。
ふ〜ん。それで、傘の指す向きとこれに、どんな関係があるの?
じゃあ、逆に聞くけど、まみは、何で傘を真上に差してたわけ?
だって、雨は上から降ってくるものでしょ。今日は風も吹いていなかったし。
うん。それがポイントかな。要するに、あたしたちが路上で止まってたら雨はまっすぐ下に降ってくるけど、動いていたら、向きが変わって見えるってこと。
う〜ん?
やっぱり図があったほうがいいよね。
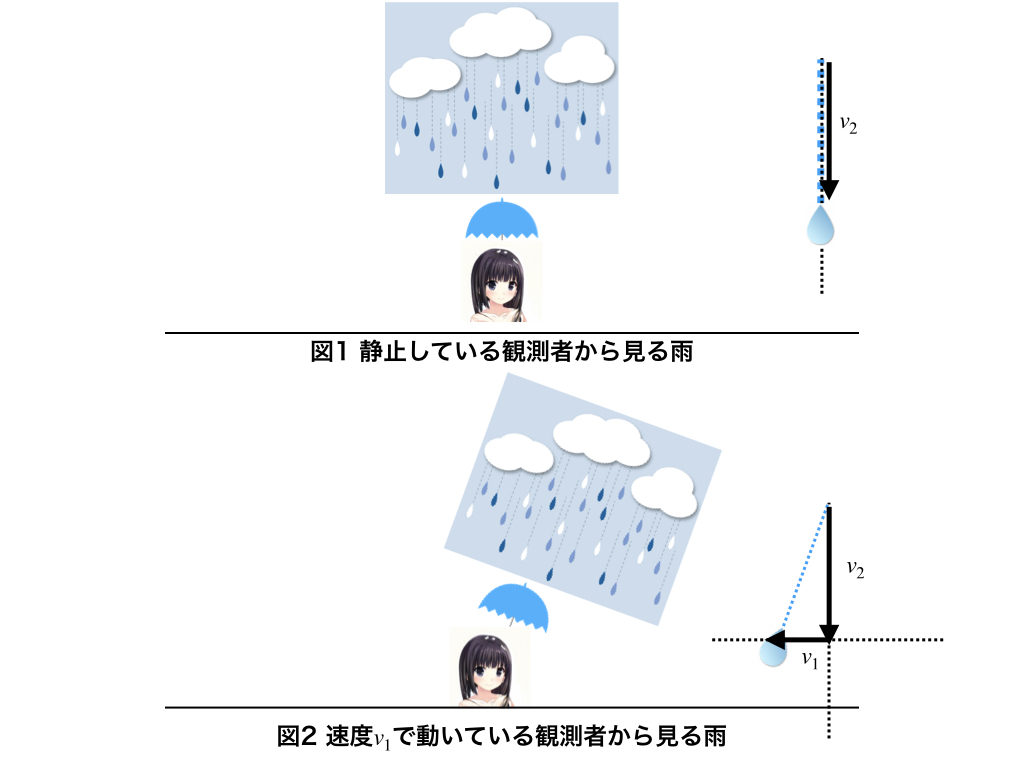
図1のように、観測者が静止していて風が吹いていなければ、雨は速度\(v_{2}\)で降ってくるとするよ。図2のように、観測者が速度\(v_{1}\)で動いているなら、雨は元々の速度\(v_{2}\)に加えて、相対速度\(-v_{1}\)の速度の二つを合成した向きに降るよね。速度の合成は、以前に説明したと思うけど、おぼえてる?
え〜と、何だっけ?
ほらぁ、三平方の定理みたいなことができるって。斜めの速度は、、、
あ、思い出した。\(\sqrt{v_{1}^{2}+v_{2}^{2}}\)のような式で書けるんだ。
そうそう。ちなみに、この場合は速度よりも角度が重要だから、雨の傾きを\(\theta\)として
$$\tan{\theta} = \frac{|v_{2}|}{|v_{1}|}$$
と書いておくよ。
ちょっと待って。\(|v_{1}|\)の棒はどういう意味だっけ?
それは、大きさ、だね。速度というのは「大きさ」と「向き」の両方をもつ量だから、その「大きさ」だけを取り出したい時は、||で挟むんだよ。\(\theta\)を出したかったら、観測者の動く速さと雨の降ってくる速さを求めればいいよね。
私は自転車で走ってたから、だいたいどのくらいかな?
だいたい、時速14kmかな。ちなみに、雨は時速25kmくらいね。これで、角度がわかるでしょ?
数学は得意だから大丈夫。三角比やってるよ。
$$\tan{\theta} = \frac{14}{25} = 0.56$$
で、三角関数表を見て、\(\tan{\theta}\)がもっとも0.56に近い角度は、、、。
三角関数表、持ってる?
持ってるよ。はい。一番右がtanね。
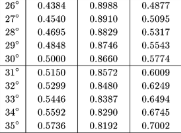
ありがと。これを見ると、角度はだいたい30°だね。
だから、傘は30°くらい傾けないとダメだったんだね。
そっか〜。ありがと、ようこ。
ていうか、自転車で傘差すの危なくない?
え〜、そうかなぁ。
歩いている人にとっては、危ないよね。
しょうがないなぁ、じゃあやめる。その代わり、ようこちゃんの家の車に、一緒に乗せてよ。
はいはい。
余計なこと言っちゃったな。

コメント