今日は、等加速度直線運動をやろっか。これやらないと、運動方程式で求めた加速度の使い道がないからね。
よろしくお願いします!
等加速度直線運動はその言葉で2つ、運動を限定しているよね。名前からわかる通り、等加速直線運動は次のような運動だね。
2. 直線の運動。
まみ、加速度の式、覚えてる?
え、え〜と、ティーツーマイナス、ティーワンぶんの、、、ベクトルブイツー、マイナス、ベクトルブイワン、とかだったかな。
そうだね。速度も加速度もベクトル量だから、本当なら向きも速さも色々変化しちゃうよね。でも、直線運動って限定しちゃえば、向きはまっすぐか、その反対方向しかない。だから、加速度の向きは速度の方向に対して「+」の向きかその反対の「−」の向きの二通りしかないね。こうやって、問題を簡単にしてるの。
なるほどね。つまり、最初の速度の向きをプラスって考えちゃえば、加速度はその方向に加速するか、減速するかしかないってことだね。本当なら、最初の運動方向に対して、斜めに進むこともあるかもしれないけど。
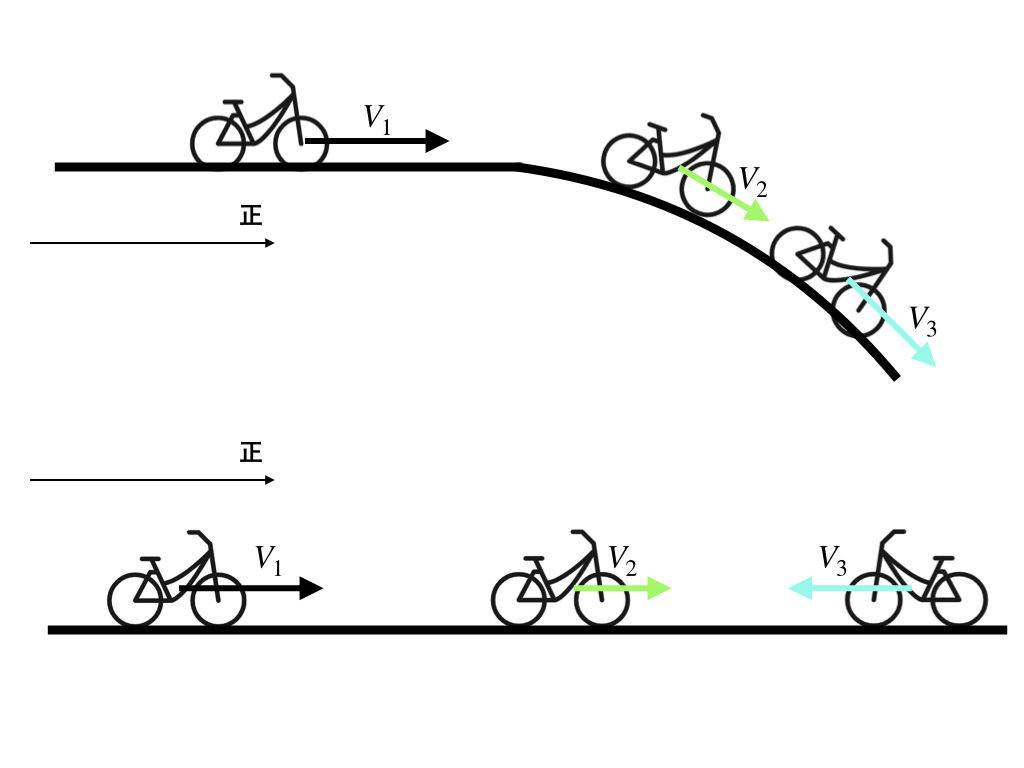
そうそう。上の図のように、もし運動が直線じゃないと、\(V_{2}, V_{3}\)の向きを計算するのが難しいよね。でも、下の図のように直線だったら、右向きを正の方向して、\(V_{1} = 3, V_{2} = 1, V_{3} = -2\)のようにマイナスをつけてあげれば、向きも含めて計算できるようになるからね。
ふむふむ。じゃあ、加速度が等しいっていうのも、問題を簡単にするためなんだね。ちなみにさぁ、もし直線運動だったら、速度と言ってもプラスとマイナスしかないんだから、加速度の式って、
$$a = \frac{V(t_{2})-V(t_{1})}{t_{2}-t_{1}}$$
みたいにベクトルとって書いていいの?
お、いいとこに気がつくじゃん。
直線運動なら、そうだね。ただし、どの方向をプラスにするか、というのはあらかじめ決めておかないとダメだよ。Vはプラスとマイナスの両方があるからね。
そっかぁ。じゃあ、加速度が等しい、というのも問題を簡単にするためなの?
うん、そうだよ。じゃあ、加速度が等しいとどういう計算ができるかを説明するよ。まず、前回言ったように、何がわかれば物体の運動を予言できるようになるか、確認するね。
はじめに、1番。加速度と\(t_{1}\)秒後の速度を使って、任意の時刻での速度を求める、ってところをやってみよう。もう一度次の式を見てみて。
$$a = \frac{V(t)-V(t_{1})}{t-t_{1}}$$
これを見て、何か気づくことはないかな。数学で習ったことだと思うけど。
ようこちゃん。それくらい朝飯前だよ。
1次関数の傾きを求める式と同じだよね。\(t\to x\), \(V\to y\)と考えれば。
この式が立てられると、求めたい\(V(t_{1})\)は次のように計算できるね。
$$V(t)-V(t_{1}) = a(t-t_{1})$$
$$V(t) = a(t-t_{1}) + V(t_{1})$$
\(t_{1} = 0\)、つまり、0秒後の速度や位置を最初の速度や位置とすると
$$V(t) = at + V(0)$$
となって、これで、任意の時刻での速度が求められるね。
1次関数の問題として解くなら、傾きがaで(t, V) = (0, V(0))を通る式、つまり、傾きがaでせっぺんが\(V(0)\)の1次関数を求めればいいんだから
$$V = at+V(0)$$
はすぐ出せるよね。
グラフも書いてみよっか。傾きが正の場合を考えるね。
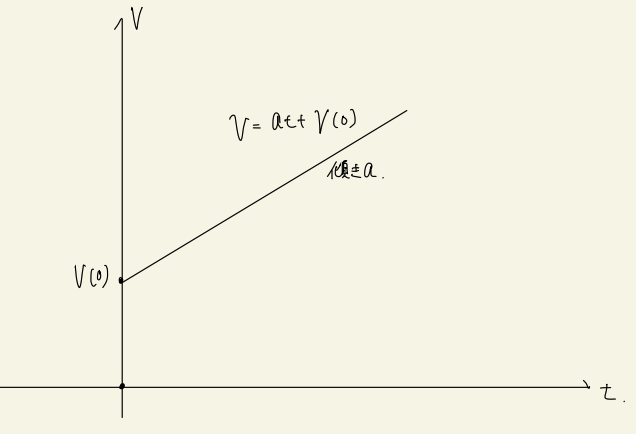
数学では\(xy\)平面だけど、物理では、tV平面? Vt平面?
物理では、よく「V-tグラフ」なんて、言ったりするよ。V-tグラフを見たら、その傾きを調べて、加速度が出せるよ。例えば、こんな感じのグラフ。まみ、\(X_{1}, X_{2}, X_{3}, X_{4}\)での加速度、求めてみてよ。
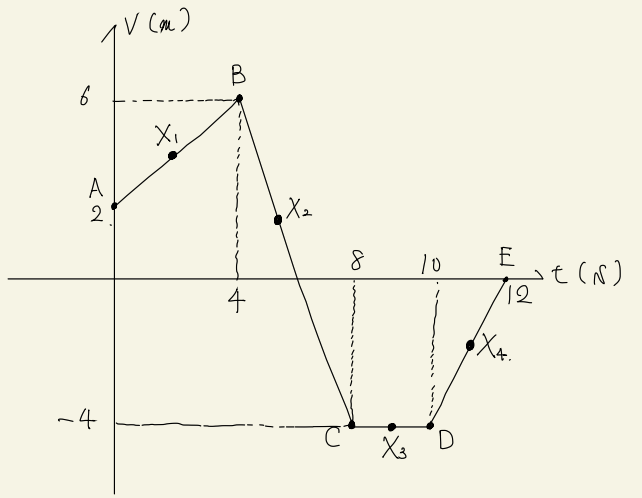
え? あたし? いいよ。
AB間の加速度、BC間の加速度、CD間の加速度、DE間の加速度を求めればいいんだよね? じゃあ、これを\(a_{AB}, a_{BC}, a_{CD}, a_{DE}\)とするね。
$$a_{AB} = \frac{(6-2)}{(4-0)} = 1\ (m/s^{2})$$
$$a_{BC} = \frac{(-4-6)}{(8-4)} = \frac{5}{2} = 2.5\ (m/s^{2})$$
$$a_{CD} = \frac{(-4-(-4))}{(10-8)} = 0\ (m/s^{2})$$
$$a_{DE} = \frac{(0-(-4))}{(12-10)} = -2\ (m/s^{2})$$
って感じかな。
でもさ、これがもし直線じゃなかったらどうするの? 例えばさ、次のような感じになったら、どうする?

この場合だと、\(X_{2}\)での加速度は、BC間の加速度を求めればいいよね。でも、\(X_{1}\)はどうするの? AB間は曲線だから、ABの加速度を求めるんじゃあ、ダメだよね。
またまた鋭いことを。曲線部分の加速度は、その点における曲線の接線の傾きが加速度に対応するよ。
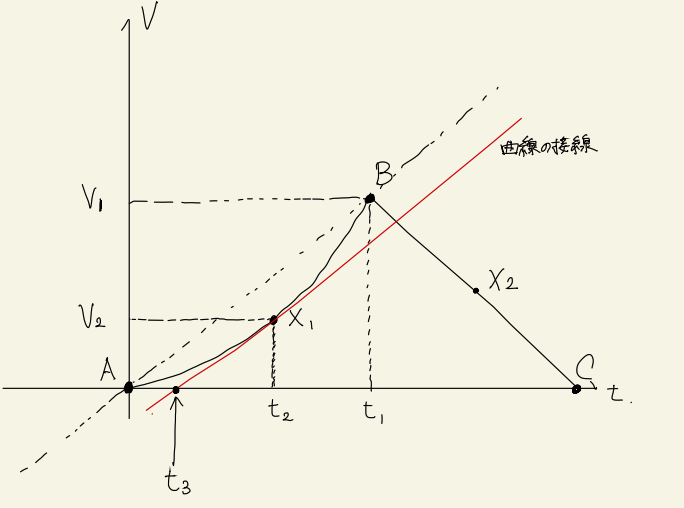
この図で、赤い線が\(X_{1}\)を通る曲線の接線なんだけど、この線の傾きが\(X_{1}\)の加速度になるよ。だから、\(t_{3}, t_{2}, V_{2}\)がわかれば加速度がわかるね。
ああ、つまり、微分! 加速度と速度って微分の関係なの?
そうなんだよね。でもその話は、ちょっと長くなるから、また次にしよう。え〜と、それで、話をどこに戻せばいいんだっけ?
加速度から速度を求めたから、次は速度から位置を求めるところじゃなかったっけ?
あ、そうだそうだ。次は「運動の予言」の2番、任意の時刻での速度と\(t_{1}\)秒後の位置を使って、任意の時刻(\(t\))での位置を求める、ってところだね。これも実はV-tグラフを使って計算できるんだ。
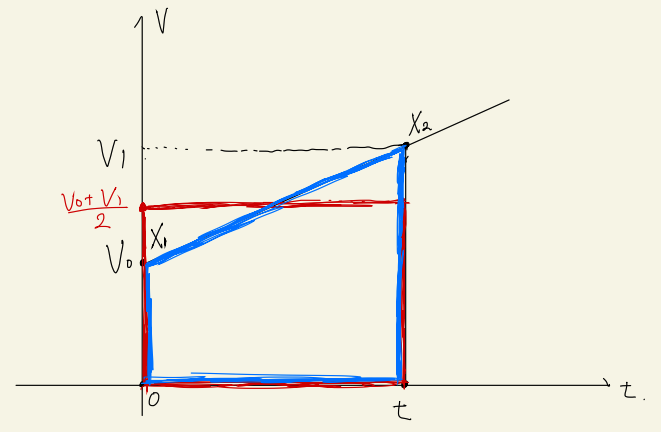
上の図で、\(X_{1}\)の地点での時間と速度が\((0, V_{0})\)で、\(X_{2}\)の地点での時間と速度が\((t, V_{1})\)とするよ。このとき、\(X_{1}\to X_{2}\)までの距離は、青色の台形の面積と同じなんだ。なんでかわかる?
赤い長方形は、青色の台形と面積が等しいんだよね?
うん。\(V_{0}\)と\(V_{1}\)の平均をとったものを高さにした長方形だよ。
赤い長方形の面積は、「時間tの間、等速度\(\frac{V_{0}+V_{1}}{2}\)で進んだ時の距離」を表していて、それが青色の面積と等しいんだから、逆に言ったら、青色の台形の面積が\(X_{1}\to X_{2}\)までの距離ってことになるんじゃない?
そういうこと。
じゃあ、今度は積分だ。
そう。等加速度直線運動って、高校物理の最初で習うんだけど、高校数学の中盤くらいで習う微分・積分が背景に隠れてるんだよ。今度、ゆっくり説明するから。
じゃあ、物体の位置を求めようよ。
そうだね。物体が最初にいた位置を\(x_{0}\)とすると、任意の時刻での位置\(x(t)\)は
$$x(t) = x_{0} + \frac{(V_{1}+V_{0})t}{2}$$
だけど、\(V_{1} = at+V_{0}\)だから、これを代入すると、
$$x(t) = x_{0} + \frac{1}{2}at^{2}+V_{0}t$$
と求められるね。
あのさ、物理の教科書とかに、「変位」とか「距離」とか「位置」とか、なんか同じような言葉が出てくるんだけど、これってどう違うの? ようこちゃん、お得意の図で、なんとかならない?
これで、どうだ!
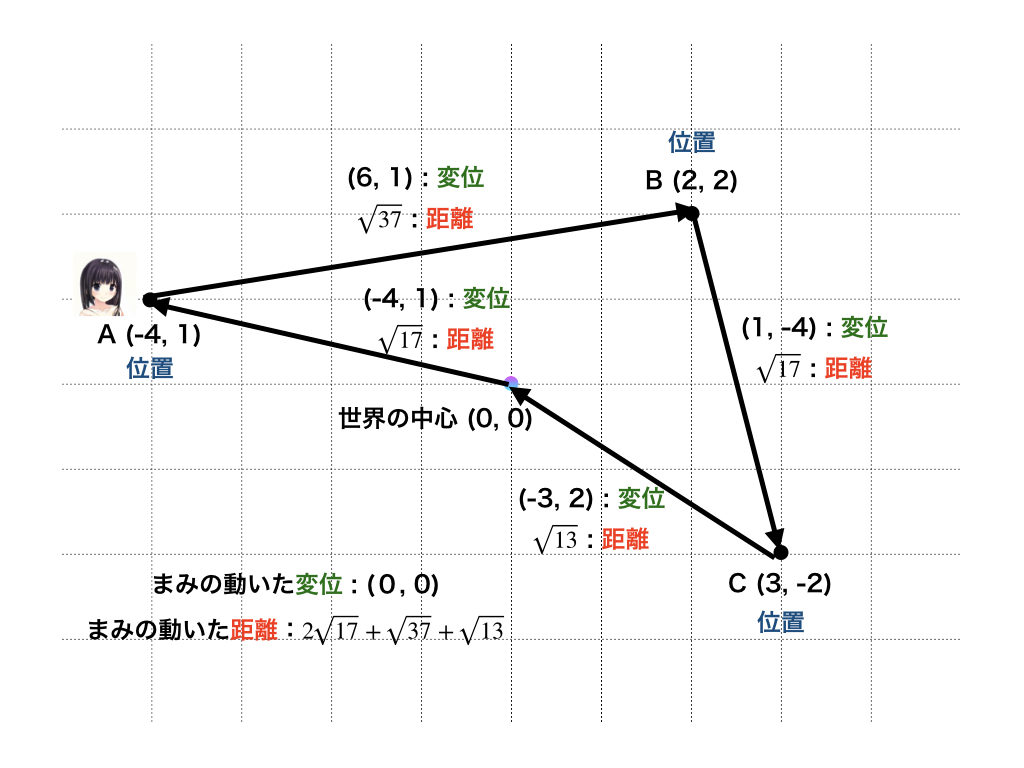
違いをわかりやすくするために、2次元での運動を考えたよ。位置・変位・距離っていうのは、全くの別物だってことがわかると思う。言葉でもまとめたよ。
Xの変位:ある位置を基準として測ったXの座標 (ある位置を基準にした時のXの位置)
XYの距離:XとYの幾何学上の長さ
うん。わかりやすい! 最後にある、あたしの変位が(0, 0)というのは、世界の中心から一周した後までの変位だよね。同じ場所から、同じ場所に戻ってきたから(0, 0)ってことね。
うん。そういうつもりだった。距離が結構あるのに、変位が0というのは少し変な感じがするかな? でも、ちゃんと位置・変位・距離の違いがわかっていれば、大丈夫だよね。ここで、問題。
$$x(t) = x_{0} + \frac{1}{2}at^{2}+V_{0}t$$
と書いた時の\(x(t)\)は位置、変位、距離のどれでしょう?
それは位置でしょ。だって、\(a, V_{0}\)はマイナスになることもあるんだから、正とは限らないし。
じゃあ、こうしたら?
$$X = x(t) – x_{0} = \frac{1}{2}at^{2}+V_{0}t$$
この\(X\)は何?
それは、変位だよ。だって、\(x_{0}\)を基準にした時の位置でしょ。
正解、正解。確かにそれは1次元での変位だね。じゃあ、また、まみにやってもらお。この\(X\)の式で、\(t\)を使わない式を書いてみてよ。
$$V_{1} = at + V_{0}$$
を使ってね。
うわぁ、めんどくさ。めんどくさいけど、最終的には、綺麗だね。
$$V^{2}_{1}-V^{2}_{2} = 2aX$$
時間がわからない時は、この式も使うことになるから、結構便利だよ。じゃあ、今まで出てきたものをまとめよっか。
1. $$V(t) = at + V_{0}$$
2. $$x(t) = x_{0} + \frac{1}{2}at^{2} + V_{0}t$$
3. $$V^{2}_{1}-V^{2}_{0} = 2aX$$
入試問題になると、この式だけじゃなくて、V-tグラフやx-tグラフを応用することが多いから、グラフを利用することに慣れておいたほうがいいよ。
おっけー。じゃあ、今度、微分とか積分とかの関係、教えてね!

コメント