ベクトルの基礎知識
今日は、速度の合成でもやる?
あ、今日はようこちゃんの番?
今日は物理やろうよ。と言っても、今日の話の大半は数学だけどね。ベクトルって話をしなきゃいけないしさ。
ようこちゃん……。あたしを誰だと思ってるのさぁ。
ベクトルくらい知ってるよぉ。
例)速さ、長さ、質量、温度、時間など
ベクトル量:大きさと向きを同時にもつ物理量
例)速度、力、電流など
色々例あるけど、速さと速度を使って説明するね。日本語では速さとか、速度とか、別に区別しないけど、物理だったらこの二つは全くの別物。速さは大きさだけで、速度は大きさと向きを持つんだよ。
あらら、知ってたか。じゃあ、一応そのまま続けてみてよ。
大きさと向きを持つっていうのは、次の図を見ればいいかなぁ。
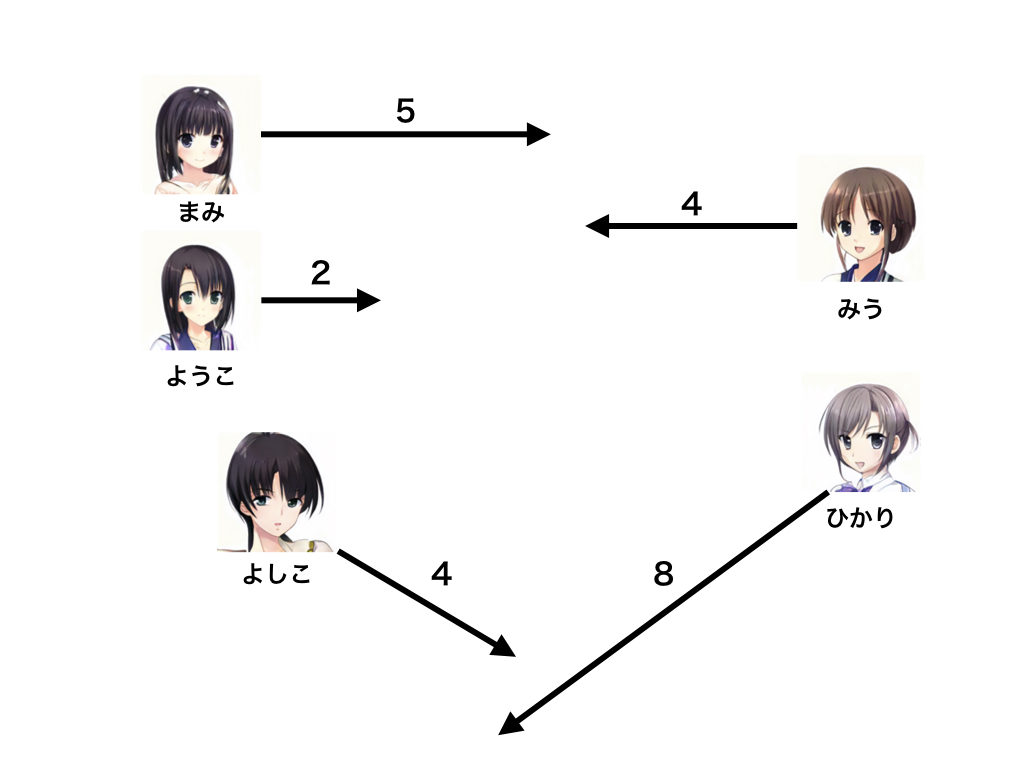
ここで書いたのは、5人が色々な向きに動く様子。速度というのは、一言でいえば「矢印そのもの」だよ。矢印の長さが速度の大きさ(速さ)で、矢印の向きが速度の向き。つまり、矢印が長いほど速いってこと。だから、物理で「速さ」と言ったら矢印の長さだけを指すの。その速さを数字で表してるって感じかな。
そう。だから、みうとよしこさんは同じ速さだけど、違う速度だってことね。
ようこちゃん、ナイス! そういうこと。みうさんとよしこさんは、同じ速さだけど向きが違うので、「速度は違う」ってこと。それでここからがポイント。
向きも考慮して足し引きする、というところがわかりづらいかな。
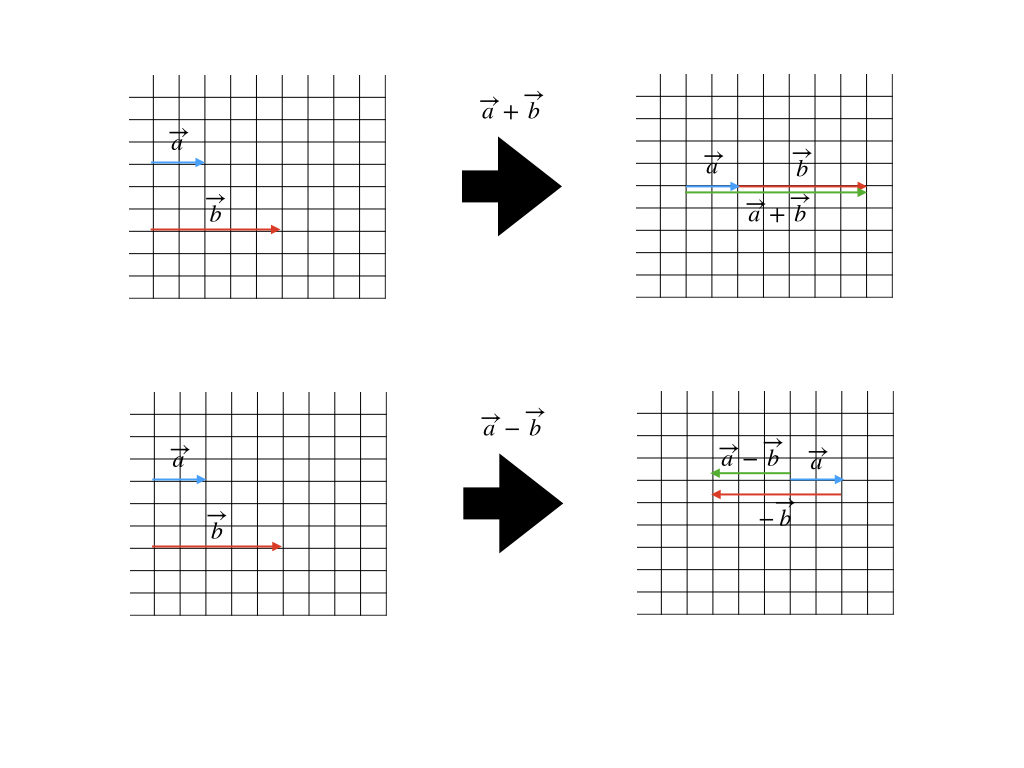
二つのベクトル量(\(\overrightarrow{a}, \overrightarrow{b}\))の減法では、マイナスの符号をついているベクトルを反対側にひっくり返して、加法と同じ操作をすれば良い。
上の図で加法を説明するよ。(\overrightarrow{b}\)の始点を(\overrightarrow{a}\)の終点に合わせる。そのあと、(\overrightarrow{a}\)の始点と(\overrightarrow{b}\)の終点を結べば、ベクトル量の加法ができる。
下の図で減法を説明するよ。まず、(\overrightarrow{b}\)の向きを反対にする。そのあと、ひっくり返した(\overrightarrow{b}\)の始点を(\overrightarrow{a}\)の終点に合わせて、(\overrightarrow{a}\)の始点とひっくり返した(\overrightarrow{b}\)の終点を結べば、ベクトル量の減法になる。わかるかな? って、ようこちゃんは知ってるんだよね。
この例では、マス目にそったベクトルなので、「大きさ」は二つの矢印の長さの足し算になったり、引き算になってるよ。
じゃあ、斜めの向きだったら?
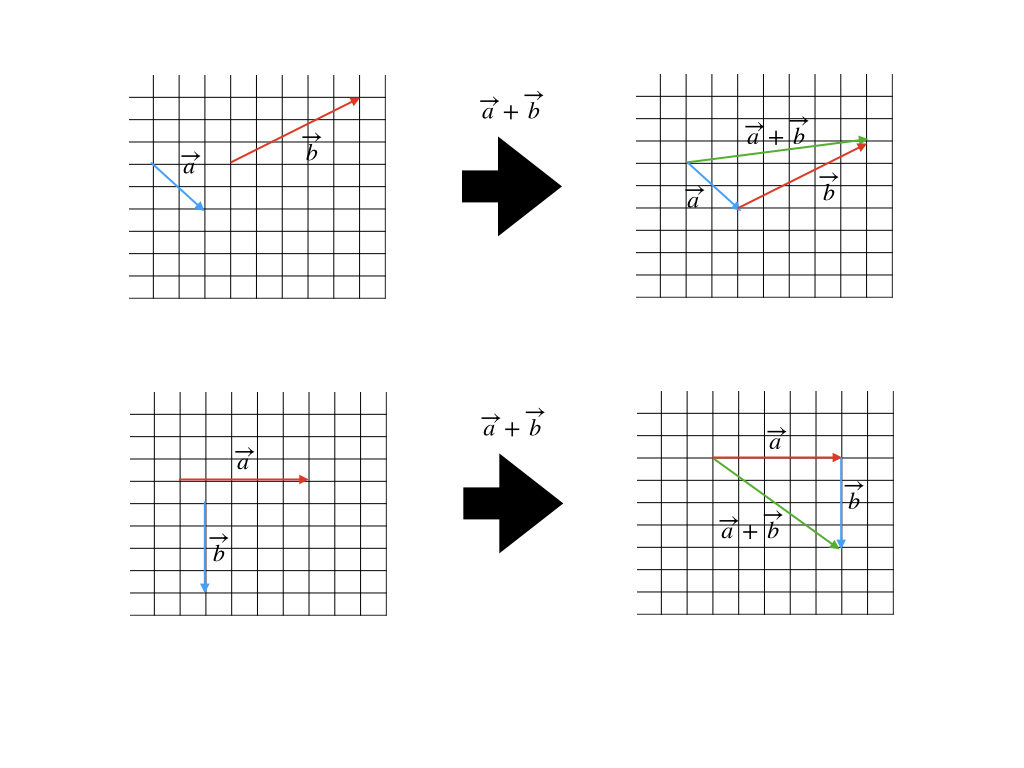
斜めでも図の上では、全く同じだよ。ただ、矢印の大きさを求める時は、少し注意が必要。上の図だったら、「余弦定理」というものを習ってから計算することができるんだけど、下の図だったらできるよね。「三平方の定理」を知っているからさ。大きさは、\(\sqrt{41}\)ってことね。
やるじゃん、まみ。
今の場合、確かに、(\overrightarrow{a}, \overrightarrow{b}\)の大きさは
$$\sqrt{4^{2} + 5^{2}} = \sqrt{41}$$
と求めることができるね
やったぁ。褒められたぁ。
まみは、数学は得意だからねぇ。
じゃあ、まとめるよ!
- ベクトル量は「大きさ」と「向き」の両方をもつ。
- ベクトル量は\(\overrightarrow{a}\)などと表し、始点と終点が命。
- (\overrightarrow{a}, \overrightarrow{b}\)の加法は、(\overrightarrow{b}\)の始点を(\overrightarrow{a}\)の終点に合わせて、(\overrightarrow{a}\)の始点と(\overrightarrow{b}\)の終点を結ぶ。
- (\overrightarrow{a}, \overrightarrow{b}\)の減法は、マイナスの符号をもつ方をひっくり返して、加法と同じ。
- ベクトル量の加法・減法の大きさは、三平方の定理などを用いて求める。
ベクトルの「速度の合成」への適用
じゃあ、ここからは私の番ね。ここからはベクトルを「速度の合成」に適用することを考えていくからね。「速度」はベクトル量なので、「速度の大きさ」と「速度の向き」を持つんだね。これらは、矢印を使って一度に表すことができる。速度の合成の話で、有名なものは、川を横切る船でしょう。
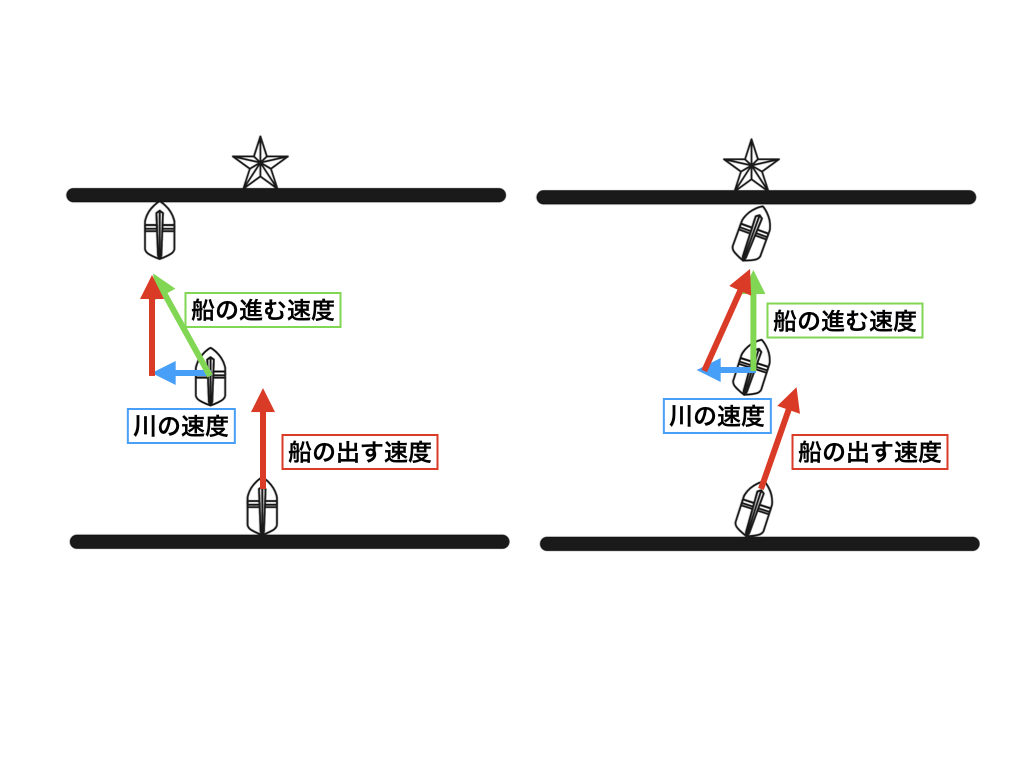
左図のように、船を目的地(星)に向かってまっすぐ進路をとって速度を出すと、川の速度の分流されてしまうよね。そこで、右図のように船をまっすぐ進ませるためには、川の速度の分を考慮して船を傾けて速度を出す必要があるね。この時、川の速度と船の出す速度を合成すると、川の速度になるの。
なるほどね〜。じゃあ、これはどう?
時速100kmで走っている車から車と逆向きに時速100kmでボールを打ち出すと、ボールはどうなる? っていう問題。Youtubeで見たことあるんだよね。
良い例だね。それも考えてみよっか。
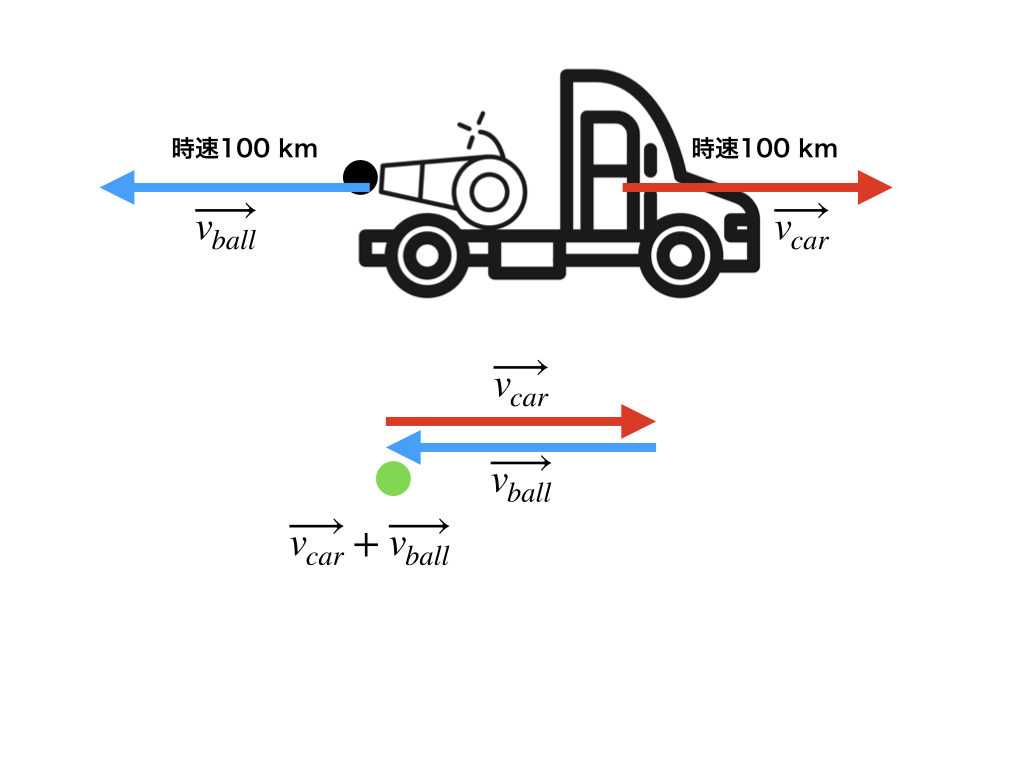
時速100 kmで走るトラックから、大砲を使って逆向きに時速100 kmで打ち出そう。車ベクトル\(\overrightarrow{v_{car}}\)の終点にボールベクトル\(\overrightarrow{v_{ball}}\)の始点を合わせる。\(\overrightarrow{v_{car}}+\overrightarrow{v_{ball}}\)は車ベクトル\(\overrightarrow{v_{car}}\)の始点とボールベクトル\(\overrightarrow{v_{ball}}\)の終点を結ぶと、、、。
点、だよね。
そう! 点。これを点ベクトルと言うんだよね。大きさも向きも0です。大きさが0なので、速度は0だよね。
おお、すごい!
でも、ようこ先生、一つ聞いていいですか。
トラックの運転手にとっては、やっぱり時速100 kmで車と反対方向に動いているように見えるよね? これってどういうこと?
鋭いね。それは、「相対速度」という考え方なの。それはまた次の話にしない?今日のところは、速度というのがベクトル量で、速度同士を足し合わせる方法について説明したかったからね。じゃあ、今日はこの辺で終わり!

コメント