ようこちゃん。物理で、運動方程式っていう方程式あるよね? これって、そんなに重要なの? 式、見てもとても簡単だし、使い道あるの?
そのたった1行の方程式で、高校物理で学ぶあらゆる運動を予言できるんだよ。
運動を予言する? 何言ってるの、ようこちゃん。
「高校物理で」っていう条件付きだけど、ね。大学に行ったら、もっと一般的な運動方程式があるんだけど・・・。
とりあえず、\(\overrightarrow{F}=m\overrightarrow{a}\)について説明してよ。予言するなんて、なんだかカッコいい。
じゃあ、まず運動方程式の形を見てみよっか。
$$\overrightarrow{F} = m\overrightarrow{a}$$
力と加速度っていうのは、ベクトル量なんだね。ところで、加速度、って何だっけ? あれ、加速度って教えてくれた?
加速度っていうのは、1秒あたりに速度がどれだけ変化したかを表す物理量だよ。式で書くとこんな感じ。
ここで、\(\overrightarrow{v}(t_{2})\)は\(t_{2}\)秒後の物体の速度、\(\overrightarrow{v}(t_{1})\)は\(t_{1}\)秒後の物体の速度を表す。
やっぱり、式だけだとわかりづらいから、図も書くね。
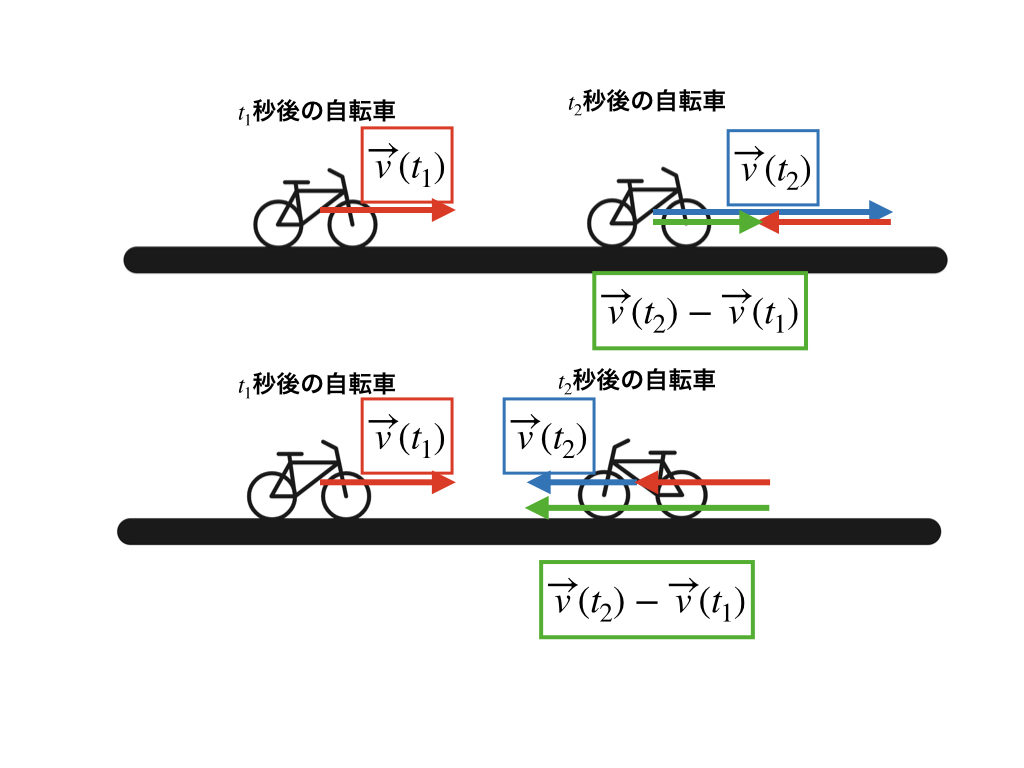
上の図から見ていくね。速度の合成でやったように、自転車の加速度は、ベクトルの減法で緑のように求められるね。もし、速度の大きさが、1秒後の1m/sから3 秒後の5m/sに変わったとすると、加速度の大きさは
$$\frac{5-1}{3-1} = 2$$
と求められて単位は2 (\(m/s^{2}\))だよね。
下の図も同じだよ。速度が、1秒後の1m/sから3 秒後の-1m/sに変わったとすると、加速度は
$$\frac{-1-1}{3-1} = -1$$
で単位をつけると、-1 (\(m/s^{2}\))って計算できるよ。
ベクトルの計算って物理では大事なんだね。
じゃあ、$$\overrightarrow{F} = m\overrightarrow{a}$$に戻るね。この式はニュートンの運動の第二法則と呼ばれてる。式を見るとわかる通り、物体に加速度がある、つまり速度を変化させるためには力が必要で、力と加速度は単に比例の形でかけるってことだね。
第二法則? 全部でいくつあるんだっけ?
ニュートンの運動法則は3つあるよ。
$$\overrightarrow{F} = m\overrightarrow{a}$$
ようこちゃん、この3つをスッキリ理解できる図はないの?
まみは図が好きだね。よし、書いてやるか。
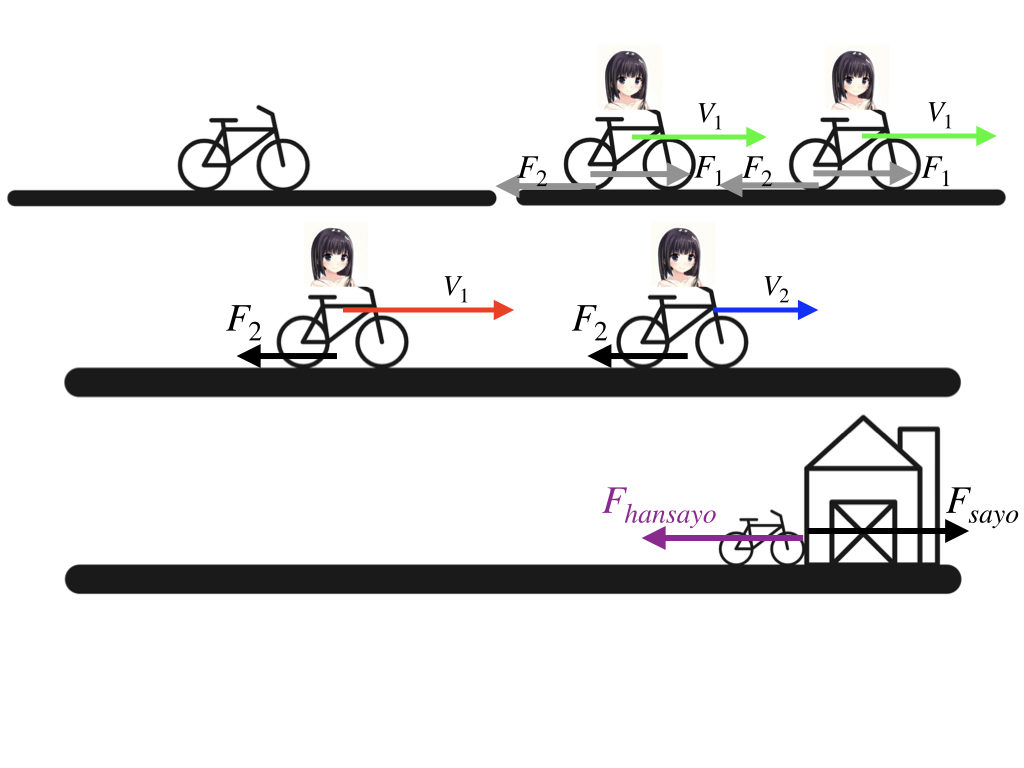
わかるかな。一番上が第一法則、真ん中が第二法則、一番下が第三法則ね。
一番上の、左の図は自転車を立ててるところかな。力がつりあっているから動かないってこと? 右は、自転車を漕いでいるけど、摩擦力をつりあって、同じ速度で動いているってことかな?
正解! じゃあ、二番目は?
これは、あたしが自転車をこいでいないから、摩擦力が勝っちゃって、自転車がどんどん遅くなってるってことでしょ。
うん。だから、加速度はマイナスってことだよね。
最後は、自転車が家に体当たりしてるよ。、、、ようこちゃん、過激な図を書くね。
あ、ごめんごめん。これがわかりやすいと思ってさ。自転車が家にぶつかると、家の方も力を受けるけど、それと同じ力が自転車にも働く様子なんだ。ちょうど作用・反作用の関係になってる。
ああ、そうか。思いっきりぶつかると、こっちも痛いもんね。
さて、またまた脱線しちゃったけど、もう一度
$$\overrightarrow{F} = m\overrightarrow{a}$$
に戻ろう。
そうだ。まだ、運動を予言する、って話を聞いてないよね。
そうだね。じゃあ、その話する? まず、運動をする物体を考えよう。予言というのは、どの時刻でその物体がどういう運動をしているかを言い当てることだとしようか。とりあえず、その物体に注目した時刻を0秒後の時刻とするね。理論上は、その物体に働く力を調べることができるよね。その力がわかれば、運動方程式を使って加速度がわかる。じゃあ、次に何がわかる?
今わかっているのは、加速度だけ?
あ、ごめん。加速度と、あと0秒後の速度もわかっているとしようか。
う〜んと、だったら、どんな時刻でも、速度が計算できるんじゃない。だって加速度の式は、
$$\overrightarrow{a} = \frac{\overrightarrow{v}(t_{2})-\overrightarrow{v}(t_{1})}{t_{2}-t_{1}}$$
という式で表されるんでしょ。ここで、\(\overrightarrow{a}\)も\(\overrightarrow{v}(t_{1})\)もわかってるんだから、\(\overrightarrow{v}(t_{2})\)もわかるはずでしょ。
さすが、まみ。鋭いねぇ。加速度、速度がわかったね。じゃあ、次は。
ようこちゃん、まだ何か忘れてない?
ははは。そうだった。0秒後の速度だけじゃなくて、0秒後の位置もわかってることにしよう。
だったら、どんな時刻での位置もわかるよね。だって速度と位置の関係って、加速度と速度の関係と同じくて、
$$\overrightarrow{V} = \frac{\overrightarrow{x}(t_{2})-\overrightarrow{x}(t_{1})}{t_{2}-t_{1}}$$
ていう感じなんだから、\(\overrightarrow{V}, \overrightarrow{x}(t_{1})\)もわかっていれば、\(\overrightarrow{x}(t_{2})\)もわかるよね。
まみは数学が絡むと強いね。普通は、そんな簡単にはいかないと思うんだけど。
えへへ、今日はよく褒められるなぁ。
今のことをまとめようか。
2. 運動方程式から、加速度がわかる。
3. 加速度と0秒後の速度から、任意の時刻での速度がわかる。
4. 任意の時刻の速度と0秒後の速度から、任意の時刻での位置がわかる。
つまり、その物体の運動(任意の時刻での位置・速度)を予言できる。
なんか、こう見るとすごいね。
$$\overrightarrow{F} = m\overrightarrow{a}$$
だけ見ると、大したことないけど、さ。
でも、こんなシンプルな形で、とても多くの運動を予言できる、ってすごいことだよ。全部の運動を予言できるわけじゃあ、ないんだけどね。
ありがと、なんか、わかった気がする。
まみは、すぐ理解してたけど、加速度から、速度、位置を出す計算は重要だから、次はこの計算をやってみようか。
え? 実際に運動方程式を使ってみるんじゃないの?
運動方程式を使っても加速度の使い方がわからないと先進まないからさ。先に、加速度の計算に慣れといたほうがいいんじゃない?
そっか。まぁ、物理はようこちゃんに任せた!

コメント