さぁ、始めよう! 東京大学の数学世界にどっぷり浸かっていくよ。
う〜ん。ちょっと楽しみだけど、やっぱり難しいんでしょ。
どうだろうね。もし、東京大学の問題に難しさ、というものがあるとするなら、それは、人の弱みみたいのを突いてくるからかなぁ。あ、意味わかる?
意味はわかるけど、イメージできないよ。
人って、当たり前だと思っていることがあると、なかなかそこから離れられないじゃん。数学の問題の中でも、無意識に当たり前だと思ってしまうと、それ以外の可能性を考えられなくなっちゃうんだよ。そうすると、例えば、複数の場合分けが必要な問題に遭遇した時、その中の1つしかイメージできずに、完全回答できなくなるってことになるよね。
ああ、そういうこと。私は、大学に受験するってだけでも緊張するのに、その状況で非常に間違えやすい計算問題をさせるってあたりが嫌味な問題だな、って思うことがあるけど。
うん。それもそうだね。特に東大は小数が好きで、度々問題に割り込んでくるよね。計算を複雑にするトリックの1つでもあるんだけど。他にも、高校数学であまり詳しく解説されないけど重要なロジック、1次独立とか実数解の条件とか必要条件・十分条件を惜しげも無く盛り込むあたり、難しいと感じてしまう要因かも。
ただね! 東京大学の問題と言っても、そのほとんどは1 stepなんだよ。たまに2 step, 3 stepの問題があるけど。
そのステップってなに?
問題の飛躍ポイントだよ。数学の問題っていうのは、それだけで完結していて、言ってみれば、問題は常に真の命題なんだ。だから、問題の中に答えが入っている。
ああ、そうかもね。つまり、全ての問題は「1+1=2」みたいなことが書いてあるのとおんなじってことか。
それはちょっと単純化しすぎだけど、あたしの要点を簡潔にまとめると、そういうことかも。で、問題のなかに答えがある、のに解けないことがある、というのは”問題”と”答え”に”飛躍”があるからだよね。この飛躍を埋めるのが受験生の仕事なんだよ。
なんかそう考えると、国語の問題と同じだよね。
あ、言われてみればそうだね。それで、その飛躍のポイントをさっき、stepと呼んだんだけど、stepが多ければ多いほど難しい問題だというのはいいよね? 一般的には、もしかすると東京大学の問題はこのstepが多いから難しいんだと思われているのかもしれないけど、それはごく一部の問題で、合格に必要な問題だけに限れば基本は1~2 stepで解けるんだよ。
へ〜、そうなの? 私もそのstepが多いから難しいんだと思ってた。
だってさ、試験時間は150分で問題が6問あるんだから、1問あたり25分だよね。回答を書く時間を5~10分だとすると考える時間はざっと15分~20分くらいしかないんだよ。東京大学の(おそらく6人の)先生は1人1問の問題を作るんだから、15~20分の思考で終わるように、手際よく解ける問題を作るはずだよ。もし、そのstepを多くし過ぎてしまうと、一部の天才を除いて、誰も解けなくなっちゃう。良い入試問題というのは、良いふるいになる問題ってことなんだから、飛躍ポイントは1~2 stepがもっとも妥当なところなんだよね。
なるほど。たまに、先生の期待と学生の学力がずれると、難問ってことになっちゃうわけだね。もしくは、意図的にstep数を増やすとか。
そうだね。各科目のバランスを取るために、難問を紛れ込ませるということもあるかもね。まぁ、大抵は、作成者の意識の中にある受験生と実際の受験生の学力に差がある場合に、難問が生まれてしまうんだと思うけど。
で、結局、あたしが言いたかったのは、東京大学の問題が難しいのはstep数ではなくてさっき言ったように、固定観念めいたものから一度脱却して他のパターンを考えるとか、見慣れない問題を見慣れた問題に直す、という作業が必要だからだと思うんだよ。とにかく、そういうことを伝えられるように頑張るよ。
ぜひ、お願いします。じゃあ、さっそく?
そうだね。今日は1961年度の問題をやろっか!
第1問 本当にそれだけか
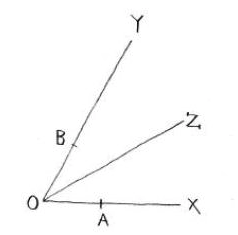
動点問題の中では非常にオーソドックスの問題だよね。実際、中学生でも解けちゃうよ。解き方は色々あると思うけど、どう解く?
この前やった、「初等幾何」「ベクトル」「座標平面」のどれを使うかってことだね。う〜ん、これは初等幾何でやりたいかな。
いいよ! この場合は座標平面でやるか初等幾何を使うのが簡単そうに見えるよね。初等幾何なら、図を書くのがいいかな。
そうだね。じゃあ、こんな感じで。
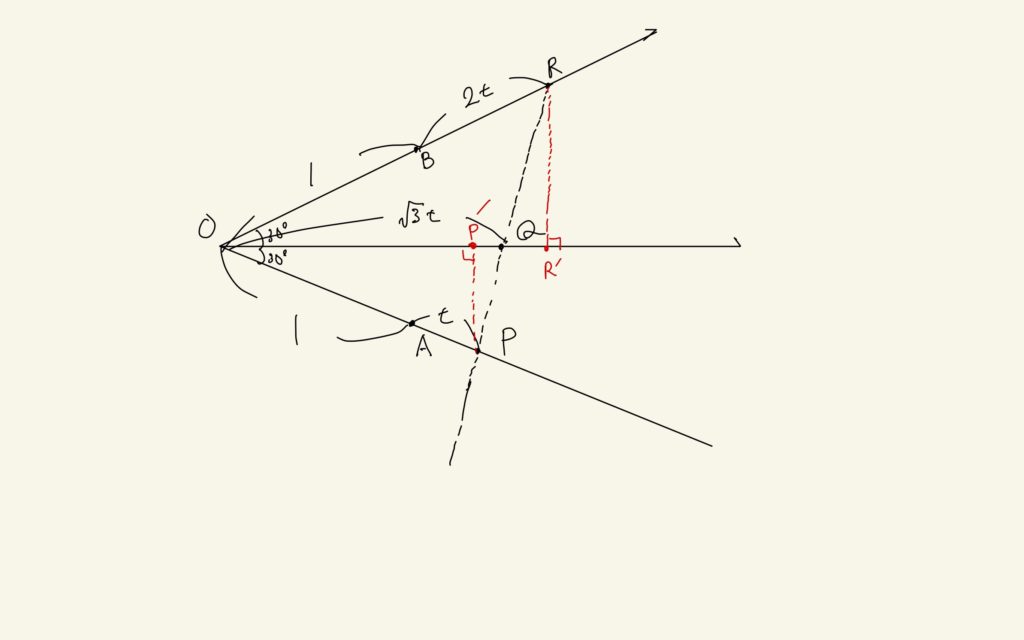
これは、問題(ⅰ)を解こうとしているわけか。\(P, Q, R\)が一直線上にある条件だね。
うん。まみのいう通り、この問題はたった1stepで解けるね。必要なのは角の二等分線定理だ。\(OR : OP = RQ : QP = 1+2t : 1+t\)で、さらに三角形の相似から\(RQ : QP = R^{\prime}Q : P^{\prime}Q\)だね。ってことは、\(R^{\prime}Q, P^{\prime}Q\)の長さが出れば解決するね。これは簡単に求まる。
うん。続けて!
$$R^{\prime}Q = OR^{\prime} – OQ = \frac{2\sqrt{3}-\sqrt{3}t}{2}$$
$$P^{\prime}Q = OQ – OP^{\prime} = \frac{\sqrt{3}t-\sqrt{3}}{2}$$
だね。あとは比の計算をすればいいね。式は、
$$ \frac{\sqrt{3}t-\sqrt{3}}{2} : \frac{2\sqrt{3}-\sqrt{3}t}{2} = 1+t : 1+2t $$
かな。これを解くと
$$t = \frac{1\pm\sqrt{5}}{2}$$
だけど、\(t>0\)だから
$$t = \frac{1+\sqrt{5}}{2} [秒]$$
が選ばれるね。
うん正解。じゃあ、もう1つの方もできる?
まぁ、同じようにやればいいよね。まずは図を描いて、、、。
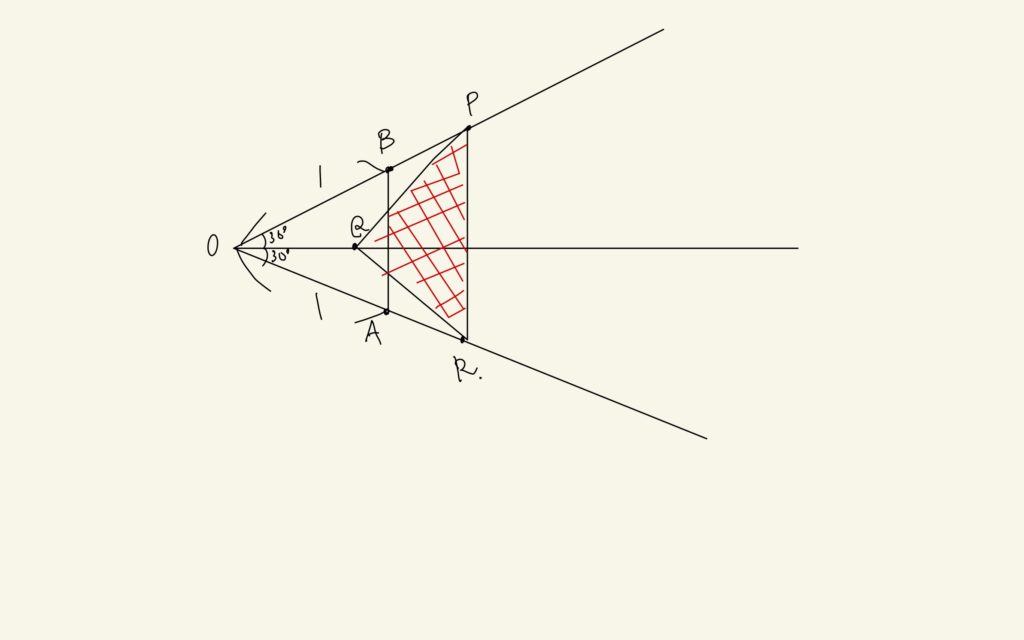
こんな感じかな。\(\triangle OAB\)の面積は1辺が1の正三角形の面積だから、\(\frac{\sqrt{3}}{4}\)だとすぐわかる。この図だと、\(\triangle PQR\)の面積は
$$\triangle PQR = \triangle OPR – (\triangle OPQ \triangle ORQ)$$
で求められるね。それぞれの三角形の面積を出すのは簡単だ。
$$\triangle OPR = \frac{1}{2}(1+t)(1+2t)\frac{\sqrt{3}}{2}$$
$$\triangle OPQ = \frac{1}{2}\sqrt{3}(1+t)\frac{1}{2}$$
$$\triangle ORQ = \frac{1}{2}\sqrt{3}(1+2t)\frac{1}{2}$$
だから、求める三角形\(\triangle PQR\)は
$$\triangle PQR = \frac{\sqrt{3}}{4}(-t^{2}+t+1)$$
になる。これが\(\frac{\sqrt{3}}{4}\)と等しいんだからその方程式を解いて
求める答えは\(t=0, 1\)だけど\(t>0\)だから\(t=1\).
お見事、と言いたいところだけど、本当にそれだけ?
ん? どういうこと?
\(P, Q, R\)の位置関係はようこちゃんが示したものだけかな?
え〜と、ちょっと待って。。。あ、違う。もう1個ある。
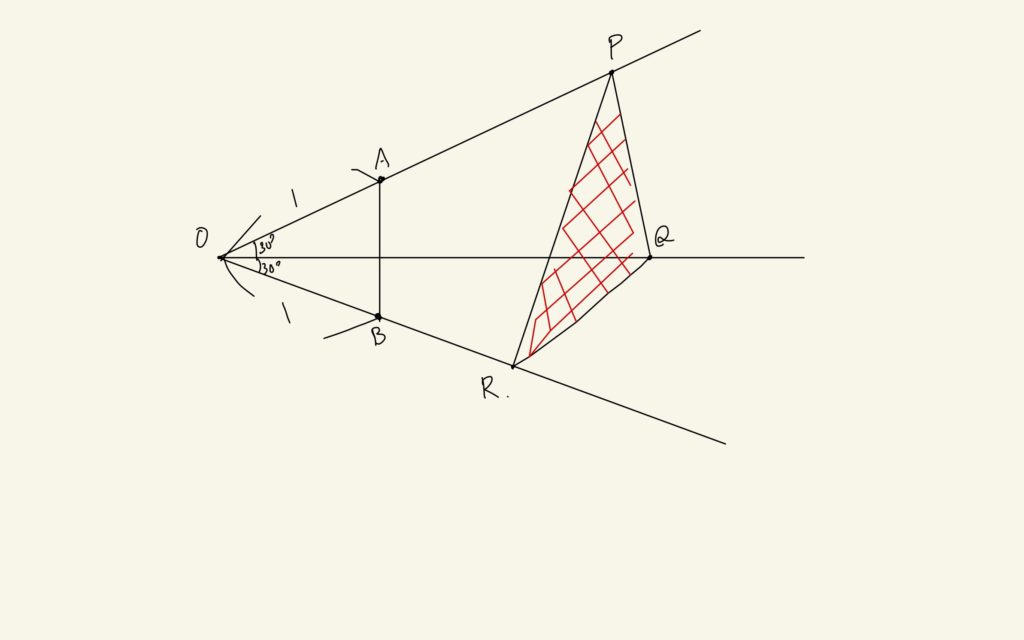
これか、、、。この場合はさっきの式、
$$\triangle PQR = \triangle OPR – (\triangle OPQ + \triangle ORQ)$$
が成り立たない。じゃなくって、こっち
$$\triangle PQR = (\triangle OPQ + \triangle ORQ) – \triangle OPR$$
にしなくちゃいけない。符号が変わるね。
そうそう。初等幾何で解く場合、こういうことに注意しないとね。考えられる全ての点の位置関係を調べて、自分で立てた式が成り立つことを確認しないとダメなんだ。
そっか〜。そうだね。ちなみに、この場合は
\(t=2\)が出てくるね。だから、\(t= 1, 2 [秒]\)が答えになるね。
うん。こんな感じで、step数は少ないけど、今回は「網羅する」というところが別のポイントだったね。
うん、見事に引っかかった。これが東大か、ならもう1問。
第2問 試される計算力
$$f(-0.2)=2.226, f(-0.1)=2.460, f(0)=2.718, f(0.1)=3.004, f(0.2)=3.320$$
なにこれ〜、小数ばっかじゃん。
そうだよ。これは混じりっけない、計算問題だね。流石に中学数学の知識じゃ解けないけど、やることはほとんど代入と計算だから、”中学数学相当”の問題とも言えるね。
え、これ、本当に代入しかないの?
う〜ん、他にもあるかもしれないけど、代入が一番手っ取り早くて簡単じゃない? ようこちゃん、がんば。
え〜、代入か。ま、なるべくわかりやすい、見やすい形で計算するよ。まず、
$$f(x) = ax^{4}+bx^{3}+cx^{2}+dx+e$$
とおくね。求めたいものは、\(f^{\prime}(0)\)ってことは、要は1次式の係数\(d\)を求めればいいってことね。じゃあ、代入するよ。っと、その前に\(f(0)=2.718\)だから\(e = 2.718\)と求まるね。お、なんか、すごくどうでもいいけど、これって自然対数\(e\)の近似値だね。
$$\begin{eqnarray}
f(-0.2)&=& 16\times10^{-4}a-8\times10^{-3}b+4\times10^{-2}c-2\times10^{-1}d+2.718 = 2.226\\
f(0.2)&=& 16\times10^{-4}a+8\times10^{-3}b+4\times10^{-2}c+2\times10^{-1}d+2.718 = 3.320\\
f(-0.1)&=& 10^{-4}a-10^{-3}b+10^{-2}c-10^{-1}d+2.718 = 2.460\\
f(0.1)&=& 10^{-4}a+10^{-3}b+10^{-2}c+10^{-1}d+2.718 = 3.004\\
\end{eqnarray}$$
いい感じだね、ようこちゃん。10の指数の形で表すのは確かに得かも。狙いは\(d\)だけだから、消し方も簡単だね。
そうだね。\(f(-0.2), f(0.2)\)と\(f(-0.1), f(0.1)\)の組み合わせで、へんぺん引けばいいんだから。そうすると慎重に計算して
$$16\times10^{-3}b+4\times10^{-1}d = 1.094$$
$$2\times10^{-3}b+2\times10^{-1}d = 0.544$$
が出てくる。ってことは、ここから\(b\)を消去して
$$d = \frac{1629}{6} = 2.715$$
となる。これが答えだ。
うん、正解。計算間違えなかったね。この問題は本当に1stepの問題で、その中身はただの計算、だけど、小数の計算を試験場で正確にできるか試した問題だね。意外とこういう問題が合否を分けたりするから、侮れないよ。
そっか〜。でも、面白みはなかったかな。ただの計算問題だもん。
おっけい。じゃあ、次行こう!
第3問 パラメタ設定の基本問題
難関大でよくある、パラメタ設定問題だね。題材もシンプルで、非常に基本的な問題だよ。
またさ、どうでもいいけど、「その高さをなにほどにすれば良いか」ってどういう日本語? 「いかほどにすれば良いか」なら、まだなんとか堪えられるけど、「なにほど」って、聞いたことないよ。古臭すぎ。
まぁ、ほら、1961年の問題だし、その辺は、ね。
うん、じゃあ、解くよ。とりあえず、これも図示から始めたい。
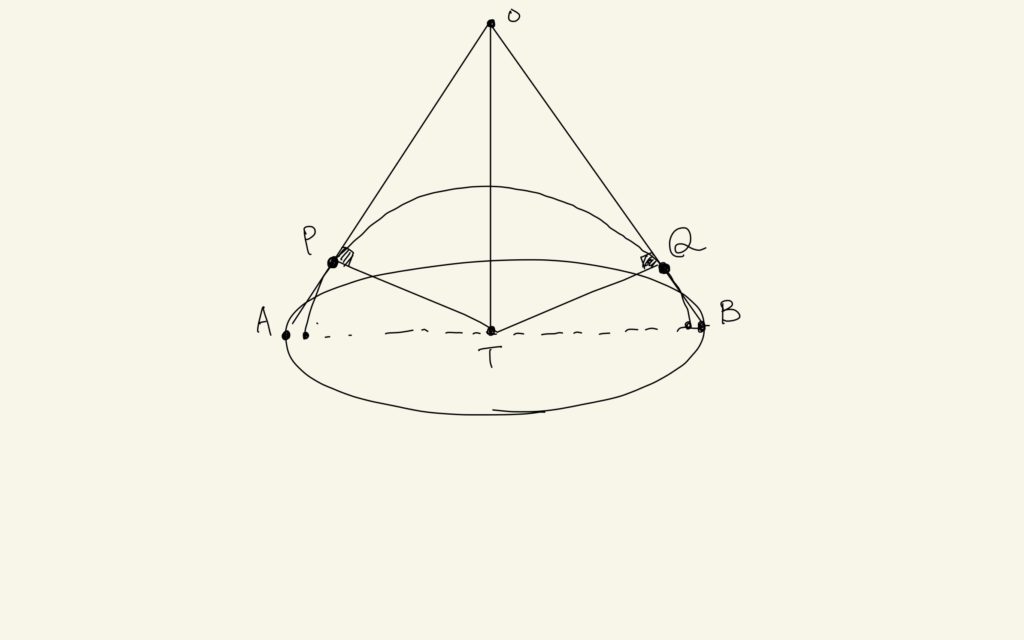
うん、問題文の言っているのは、こういう図だよね。
ようこちゃんは、どうやってパラメタをとる?
私なら、こう。
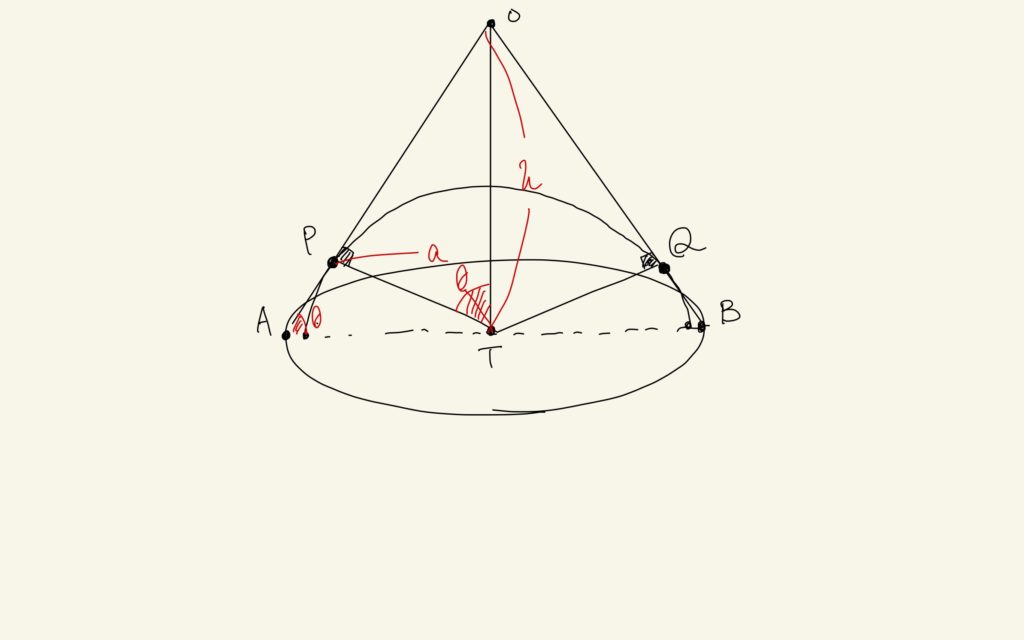
なるほど、そうだね。高さは当然として、もう1つを角度に設定するのが基本だね。東大でも京大でも、角度をパラメタにすると綺麗に計算できることが多いから。じゃあ、そのまま続けられる?
ここまで見えちゃえば、あとは直円錐の全表面積を求めればいいわけだから、できそうかな。直円錐の表面積は扇型の面積(P)と底面の円の面積(S)の和(T)だね。
この図にさらに長さを書き足していくと、こうなる。
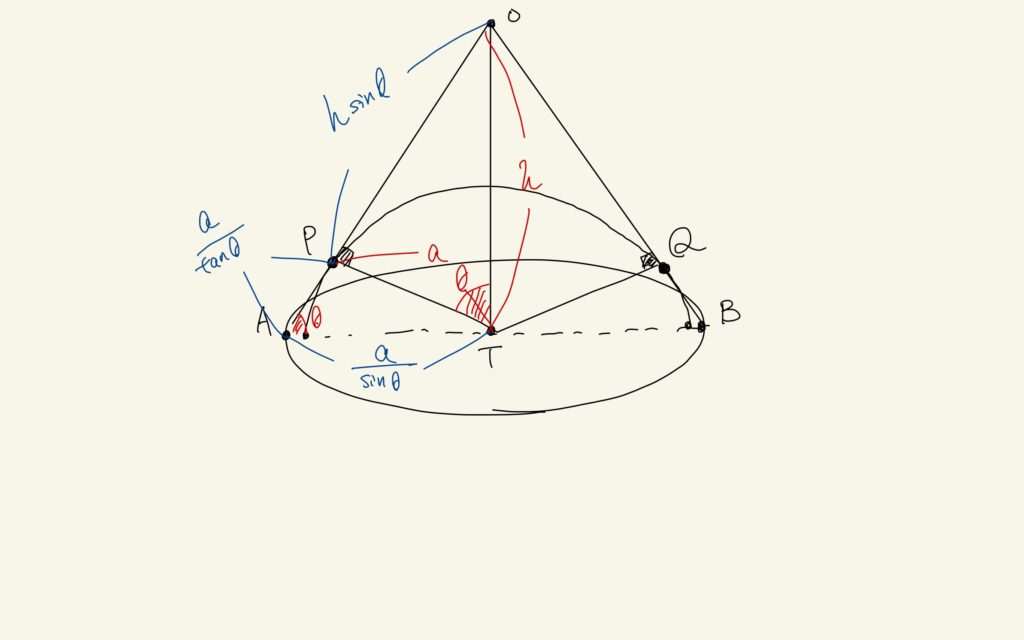
まず、扇型の面積Pから。
$$P = \frac{1}{2}\left( \frac{2\pi a}{\sin{\theta}} \right)\left( \frac{a}{\tan{\theta}+h\sin{\theta}} \right)$$
次に底面積Sは
$$S = \pi a^{2}\frac{1}{\sin^{2}{\theta}}$$
だから全表面積Tは
$$T =\frac{1}{2}\left( \frac{2\pi a}{\sin{\theta}} \right) \left( \frac{a}{\tan{\theta}}+h\sin{\theta} \right) + \pi a^{2}\frac{1}{\sin^{2}{\theta}}$$
快調な出だし。
問題は、\(h, \theta\)のどっちを消去するか、だね。微分して最小値を議論したいから1文字減らしたい。
そうだね、実際、\(h\cos{\theta} = a\)という式があるからね。
私はやっぱり角度を残して計算したいなぁ。だから、\(h\)を消す。
うん、うん。いいんじゃない。
そうすると
$$T = \pi a^{2}\frac{1}{\sin^{2}{\theta}} + \pi a^{2}\left( \frac{\cos{\theta}}{\sin^{2}{\theta}}+\frac{1}{\cos{\theta}} \right) $$
だから、いっそ両辺を\(\pi a^{2}\)で割っちゃおう。
$$\frac{T}{\pi a^{2}} = \frac{1}{\sin^{2}{\theta}} + \frac{\cos{\theta}}{\sin^{2}{\theta}}+\frac{1}{\cos{\theta}}$$
これを最小にすればいいんだ。あ、待って、これもっと簡単になる。通分すると
$$T = \frac{1+\cos{\theta}}{\sin^{2}{\theta}\cos{\theta}}$$
だから、これを微分した方が簡単かな。
微分するときは、なるべく簡単な式にした方がお得だもんね。
よし、じゃあ、微分するぞ。。。
うん、最終的にはこんな形になる。
$$T^{\prime} = \frac{-\sin{\theta}(\cos{\theta}+1)^{2}(2\cos{\theta}-1)}{(\sin^{2}{\theta}\cos^{\theta})^{2}}$$
うん、増減表を書けばはっきりするけど、\(\cos{\theta}=\frac{1}{2}\)の時に最小だね。だから、求める高さは
$$h = \frac{a}{\cos{\theta}} = 2a$$
となる。どう?
うん、バッチリ。この問題も飛躍ポイントは少ないね。せいぜい、パラメタ表示にする1stepかな。あとは、条件通りに丁寧に計算していけば解けちゃう基本問題だよ。
この年の問題は、すごく易しめに作られていたのかな?
計算問題をやさしいと考えるかどうかは難しい問題だけど、少なくともひらめきやすごい発想なんて全くいらないね。高校数学を汗水垂らして計算していた人が勝つような問題。ただ、次の問題はどうかな?
第4問 平面図形の真骨頂
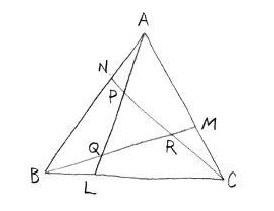
この問題、京大の平面図形・ベクトルを制覇したあたしたちなら、楽勝かな?
どうかなぁ? ベクトルを使いながらところどころ初等幾何を使っていけばできそうだけどね。やり方によって、中学生でもできるかな。てか、そういう問題多いなぁ、今年のは。
じゃあ、まずは図からだね。
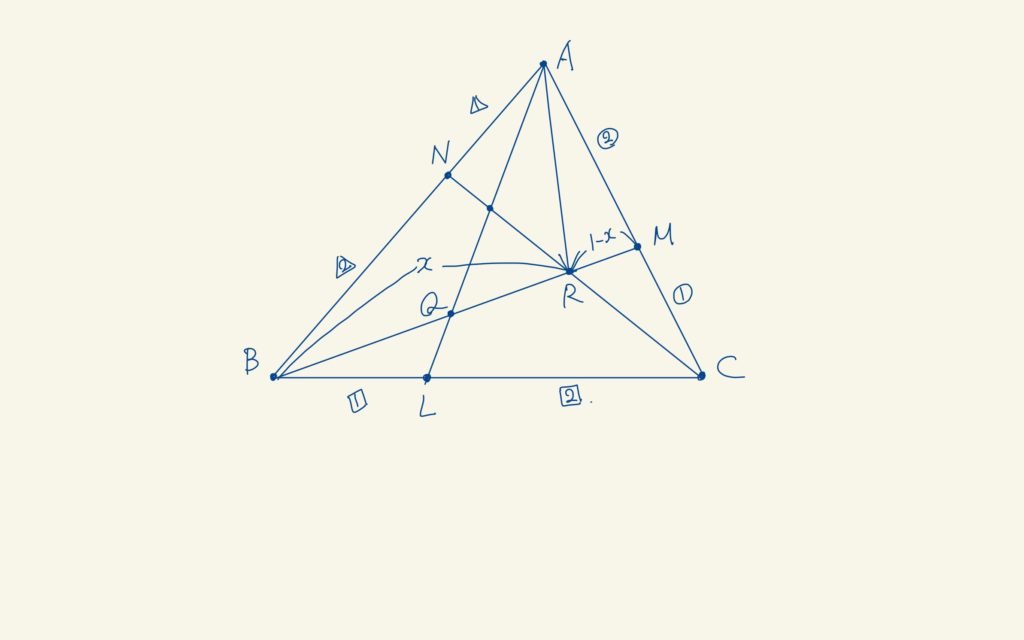
まず、\(x\)を求めようかな。あ、いや待って。その前にメネラウスの定理が使えるから、それで、先に\(CR : RN\)を求めておくと簡単かも。
$$\frac{CM}{MA}\times\frac{AB}{BN}\times\frac{RN}{CR} = 1$$
$$\frac{RN}{CR} = \frac{4}{3}$$
だから、\(CR : RN = 3 : 4\)だね。これでベクトルを使おう。
$$\overrightarrow{AR} = (1-x)\overrightarrow{AB} + \frac{2}{3}x\overrightarrow{AC} = \frac{1}{7}\overrightarrow{AB} + \frac{1}{4}\overrightarrow{AC}$$
\(\overrightarrow{AB}, \overrightarrow{AC}\)は1次独立だから、係数比較ができて、\(x = \frac{6}{7}\)だね。じゃあ、今までの結果をまとめる。
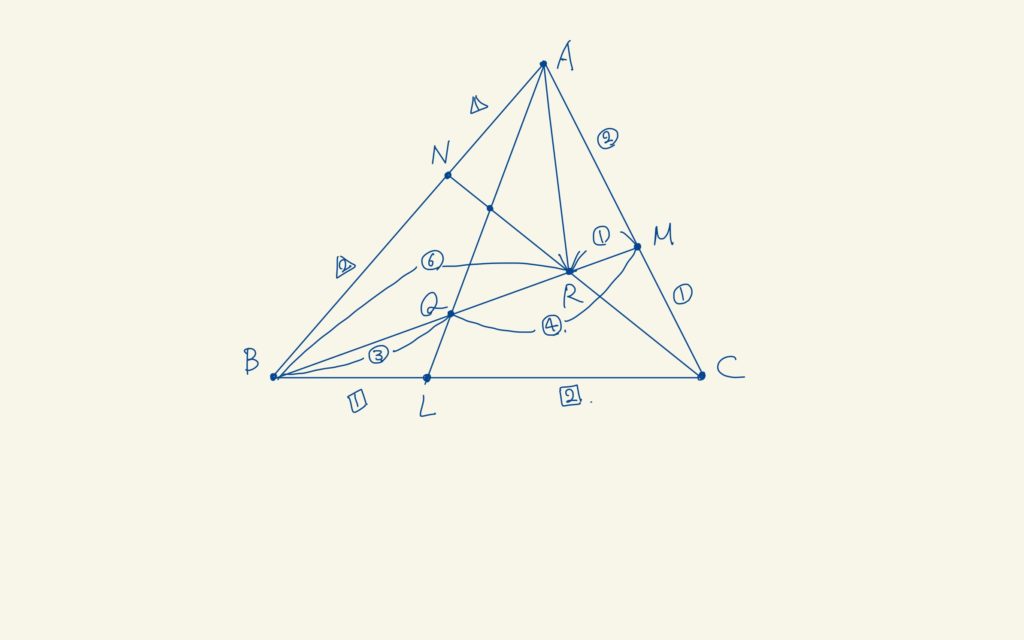
さすが、ようこちゃん。百戦錬磨の解き筋だね。ちなみに、対称性を使うとさらにここまでわかるよね。
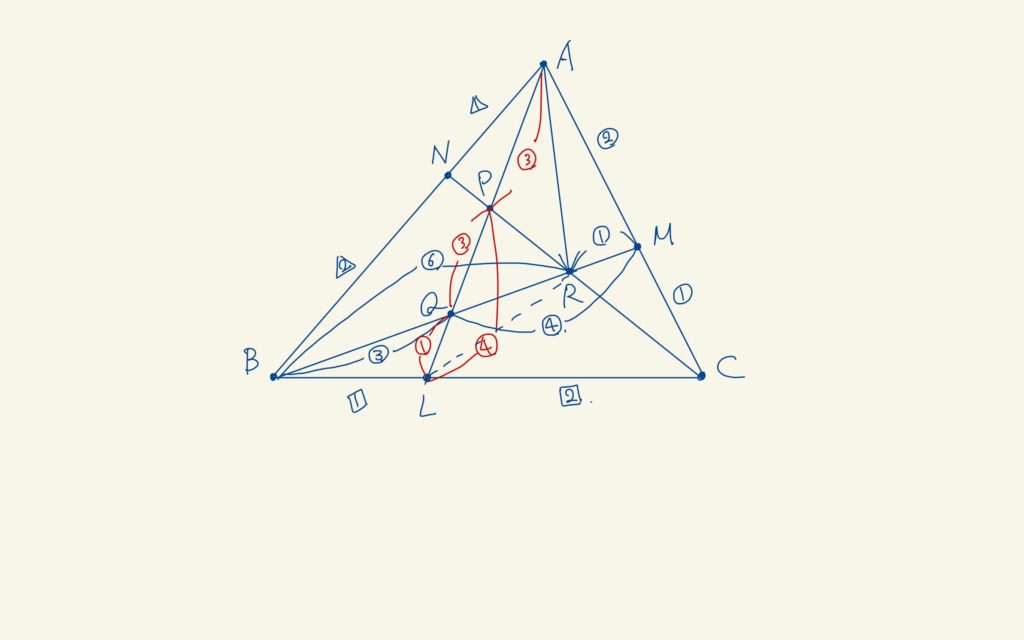
ありがとう、まみ。
あとは辺の比を使って面積比を求めていけばいいね。丁寧に計算するよ。
$$\begin{eqnarray}
\triangle{ALC} &=& \frac{2}{3}\triangle{ABC} \\
\triangle{CLP} &=& \frac{4}{7}\triangle{ALC} \\
\triangle{PRL} &=& \frac{1}{2}\triangle{CLP} \\
\triangle{PQR} &=& \frac{3}{4}\triangle{PRL} \\
\end{eqnarray}$$
だから、\(\triangle{ABC}, \triangle{PQR} \)の関係は
$$ \triangle{PQR} = \frac{2}{3}\times \frac{4}{7}\times \frac{1}{2}\times \frac{3}{4}\triangle{ABC} = \frac{1}{7}\triangle{ABC}$$
となって、求める面積は\(1:7\)かな?
はい、またまた正解。ようこちゃん完璧。
う〜ん、まぁでも、今はリラックスして解いているからね。本番はもっと緊張していて、さっきの計算だって間違えそう。
いやいや、ようこちゃんなら大丈夫だって。さぁ、いよいよあと2問。ようこちゃん、まだ元気ある?
う〜ん、そろそろしんどいかも。ちょっと助っ人を、、、。
え? 助っ人か。といっても、次の問題は数Ⅲ範囲の問題なんだけど、どうしよう。あ! ちょうどよかった。あそこに、みよちゃんがいるじゃん。ちょっと呼んでくる。
まみ、何か用?
ちょっとこの問題を見てもらいたいんだけど。
・・・・・・。これ、理系の問題じゃん。あたしは文系だよ。
そんなこと言って解けるくせに。お願いだから、計算してよ。
めんどくさいなぁ。じゃあ、その代わりにあたしの宿題やっといてよ。これ解いたらまた寝るからさ。
え、う、うん。やるよ、きっと。ようこちゃんが。
お〜い。
わかった。じゃあ、解くよ。
第5問 もどる曲線には要注意
媒介変数表示のまま計算するよ。
$$\frac{dx}{dt} = 2t, \frac{dy}{dt} = 2t+1$$
だから、増減表は以下。
| \(t\) | \(\cdots\cdots\) | \(-\frac{1}{2}\) | \(\cdots\cdots\) | 0 | \(\cdots\cdots\) |
| \(\frac{dx}{dt}\) | – | – | 0 | + | |
| \(x\) | ↘︎ | \(\frac{5}{4}\) | ↘︎ | ↗︎ | |
| \(\frac{dy}{dt}\) | – | 0 | + | ||
| \(y\) | ↘︎ | \(-\frac{9}{4}\) | ↗︎ | ↗︎ |
これと、\(t = 1, -2\)の時に\(y=0\)になることに注意してグラフを描く。
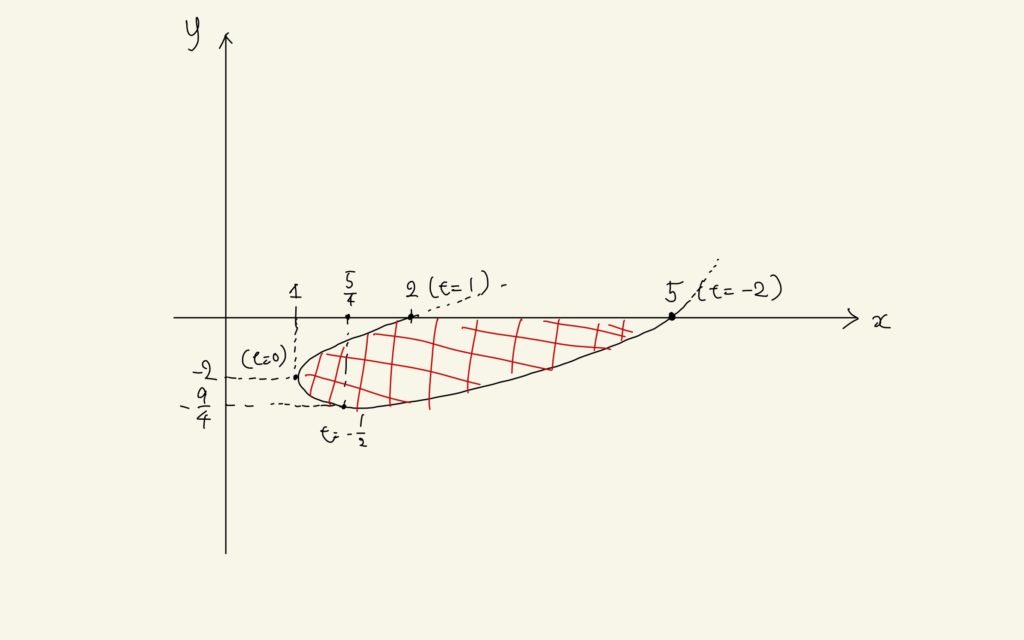
あとは積分するんだけど、、、。
媒介変数表示の積分は数Ⅲで習うけど、数Ⅱまででも
\(S = \int_{a}^{b} f(x)dx\)
で面積が求められることは習っているね。
媒介変数の場合は
\(S = \int_{\alpha}^{\beta} f(t) \frac{dx}{dt}dt\)
として求められる。だけど、この場合はちょっとめんどくさい。
$$S = -\int_{5}^{1}ydx -\left( -\int_{1}^{2}ydx \right)$$
を計算することになる。
あ、そうか。
$$ -\int_{5}^{1}ydx$$
の部分は、折れ曲がる前の曲線を使った面積。マイナスが付いているのは、曲線が負の領域にあるからだね。
$$-\left( -\int_{1}^{2}ydx \right)$$
は折れ曲った後の曲線を使った面積。
それぞれを引かないとダメだったね。
これを書き換えると
$$S = -\int_{0}^{-2}y(t)\frac{dx}{dt}dt + \int_{0}^{1}y(t)\frac{dx}{dt}dt$$
となる。具体的に代入すると
$$S = -\int_{0}^{-2} (2t^{3}+2t^{2}-4t) dt + \int_{0}^{1} (2t^{3}+2t^{2}-4t) dt$$
で、結局
$$S = \frac{9}{2}$$
みよちゃん、さすが。理系の問題なのに、問題ないね。
はい、じゃあ、約束。宿題、ここにおいとくね。あとはよろしく。
え、結構ある。。。
ようこちゃん、よろしく!
それはあとで相談するとして、あと1問でしょ。
あ、そうだ。じゃあ、そっちを先に。
第6問 たった1step
$$\int_{0}^{2\pi}f(x)\cos{x}dx = 5\pi$$
である。このとき
(1) \(a, b, c\)を求めよ。
(2) \(0\leq x\leq 2\pi\)の範囲で\(f(x)\)を最小にする\(x\)の値とそのときの\(f(x)\)の値とを求めよ。
さぁ、最後はまたしても積分だ。今度は三角関数の積分だけど。
計算していけば自然に解けそうだね。最後だし、頑張って計算するか。
まず、
$$f\left( \frac{\pi}{4} \right) = \frac{\sqrt{2}}{2}a+\frac{\sqrt{2}}{2}b + c = 6\sqrt{2}$$
が成り立つ。次に、\(f(x)\)を微分すると
$$f^{\prime}(x) = a\cos{x}-b\sin{x}+2c\cos{2x}$$
だから
$$f^{\prime}\left( \frac{\pi}{4} \right) = \frac{\sqrt{2}}{2}a-\frac{\sqrt{2}}{2}b = 0$$
で\(a=b\)が成り立つ。あとは、積分の式を計算するだけ。
$$\begin{eqnarray}
&&\int_{0}^{2\pi}(a\sin{x}+b\cos{x}+c\sin{2x})\cos{x}dx\\
&=& a\int_{0}^{2\pi}\sin{x}\cos{x}dx + b\int_{0}^{2\pi}\cos^{2}xdx+c\int_{0}^{2\pi}\sin{2x}\cos{x}dx
\end{eqnarray}$$
最後の式で、第1項と第3項は0になるから第2項だけ計算すればいい。
$$b\int_{0}^{2\pi}\cos^{2}xdx = b\left[ \frac{\frac{1}{2}\sin{2x}+x}{2} \right]_{0}^{2\pi} = b\pi$$
だから、\(b=5\)になる。他の式を使っていくと、\(a=5, c=\sqrt{2}\)
うん、正解!
じゃあ、次は本当に最後の問題だね。
長かったなぁ。でもあとは微分して増減表描くだけだよね。
$$f^{\prime}(x) = 5\cos{x}-5\sin{x}+2\sqrt{2}\cos{2x}$$
ん? これ因数分解できる?
ここだね。ここが唯一のstep。ここをクリアできたら、あとはおなじみの計算で答えがでる。さぁ、ようこちゃん、これをどう因数分解する?
う〜ん、\(\cos{2x}\)は\(\sin\)にも\(\cos\)にも置き換えられるけど、どっちにしてもどっちかが残っちゃうなぁ。
悩んでるねぇ。\(\cos{2x}\)を表すもう一つの表現があるんだけど、ようこちゃんは知っているかな?
もう一つ? \(\sin, \cos\)を両方用いる方法? あ! そういえば
\(\cos{2x} = \cos^{2}{x} – \sin^{2}{x}\)だっけ。なるほど、これなら因数分解できそう。
$$f^{\prime}(x) = (\cos{x}-\sin{x})(5+2\sqrt{2}(\cos{x}+\sin{x}))$$
よし、増減表が書ける。
| \(x\) | 0 | ‥‥‥ | \(\frac{\pi}{4}\) | ‥‥‥ | \(\frac{5\pi}{4}\) | ‥‥‥ | \(2\pi\) |
| \(\frac{dy}{dx}\) | + | 0 | – | 0 | + | ||
| y | 5 | ↗︎ | \(6\sqrt{2}\) | ↘︎ | \(-4\sqrt{2}\) | ↗︎ | 5 |
ってことで最小値は
$$-4\sqrt{2},\ (x = \frac{5\pi}{4} )$$
ってことだね。
うん、大正解。
まみに助けてもらったけどね。
でもほとんどようこちゃんが解いたんだよ。
この年の問題、どうだった?
う〜ん、計算ばっかでめんどくさいって感じだったな。
難しい、って感じはなかったけど。
そうだよね。他の年の問題を見るとわかるけど、もちろん、難しい問題もある。でも、大抵は可能性を網羅することと、計算能力、オーソドックスな解法を頭に入れておけば、解き切れるはず。
そうだね、ちょっとやれそうな気がしてきた。
じゃあ、今日はこの辺で終わり! みよちゃんの宿題、頼んだ!
あ、ちょっと、まみ!
相談するって言ったでしょ、待ってよ。



コメント